Доверительные интервалы при нормальном распределении случайной величины
Пусть случайная величина Х распределена по нормальному закону (закону Гаусса) с математическим ожиданием M и среднеквадратичным отклонением s. Математическое ожидание M является истинным значением случайной величины Х.
Определим вероятность неравенства.
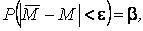 (3.62)
(3.62)
где 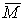 – оценка математического ожидания;
– оценка математического ожидания;
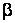 – доверительная вероятность;
– доверительная вероятность;
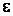 – ошибка от замены M оценкой
– ошибка от замены M оценкой 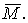
Параметры распределения случайной величины 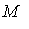 и
и 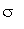 неизвестны, поэтому решить уравнение (3.62) невозможно.
неизвестны, поэтому решить уравнение (3.62) невозможно.
Поделим обе части неравенства 
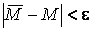 на
на 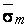 ,
,
где  – исправленное среднеквадратическое отклонение, определяемое из опытных данных;
– исправленное среднеквадратическое отклонение, определяемое из опытных данных;
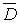 – статистическая дисперсия;
– статистическая дисперсия;
n – число опытов.
Получим:
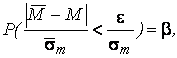 (3.63)
(3.63)
или
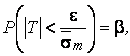
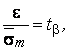
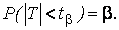
Случайная величина Т подчиняется распределению Стьюдента.
Дифференциальная функция распределения имеет вид:
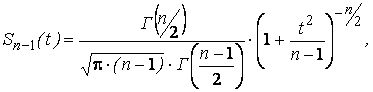
где 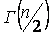 – гамма-функция
– гамма-функция
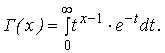
Распределение Стьюдента зависит от числа опытов или, что то же самое, от числа степеней свободы 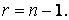
Распределение Стьюдента позволяет найти решение уравнения (3.62).
Величина 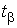 , называемая квантилем распределения Стьюдента, определится из условия
, называемая квантилем распределения Стьюдента, определится из условия
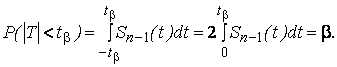
Функция 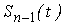 – четная, поэтому
– четная, поэтому 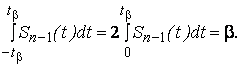
Квантилем, отвечающим заданному уровню вероятности b, называют такое значение 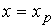 , при котором функция принимает значение, равное b, т. е.
, при котором функция принимает значение, равное b, т. е. 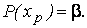
Квантиль tb находим из таблицы распределения Стьюдента, в зависимости от доверительной вероятности и числа степеней свободы 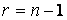 .
.
Величина e, равная половине длины доверительного интервала, определится по формуле
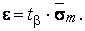
Доверительные интервалы для оценок параметров рассчитываются следующим образом.
1. Задаются доверительной вероятностью 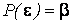 . Обычно b = 0,8; 0,9; 0,95; 0,99.
. Обычно b = 0,8; 0,9; 0,95; 0,99.
2. Определяется число степеней свободы 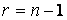 , где n – число опытов или наблюдений.
, где n – число опытов или наблюдений.
3. Из таблицы распределения Стьюдента по заданным r и b находят квантиль 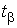 .
.
4. Из опытных данных определяется исправленное среднеквадратическое отклонение:
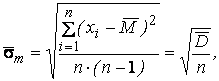
где 
5. Половина длины доверительного интервала определяется по формуле:
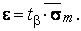
6. Доверительный интервал будет: