Равномерное, нормальное и показательное распределение

1. Цена деления шкалы амперметра равна 0,1 А. Показания округляют до ближайшего целого деления. Найти вероятность того, что при отчёте будет сделана ошибка, превышающая 0,02 А.

2. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отчёте будет сделана ошибка: а) меньшая 0,04; б) большая 0,05.

3. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 5 минут. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобуса менее 3 минут.

4. Минутная стрелка электрических часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на 20 с.

5. Закон равномерного распределения задан плотностью вероятности 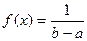в интервале (a, b); вне этого интервала 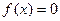. Найти функцию распределения .

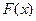6. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X, распределенной равномерно в интервале (2, 8).

7. Равномерно распределённая случайная величина X задана плотностью распределения 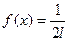в интервале (a-l, a+l); вне этого интервала 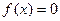. Найти математическое ожидание и дисперсию X.

8. Математическое ожидание нормально распределённой случайной величины X равно m_x=3 и среднее квадратическое отклонение σ=2. Написать плотность вероятности X.

9. Написать плотность вероятности нормально распределённой случайной величины X, зная, что M(X)=3, D(X)=16.

10. Нормально распределённая случайная величина X задана плотностью 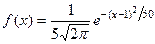. Найти математическое ожидание и дисперсию X.

11. Написать плотность и функцию распределения показательного закона, если параметр λ=5.

12. Найти параметр λ показательного распределения: а) заданного плотностью 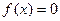при x<0, 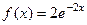при x≥0; б) заданного функцией распределения 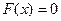при x<0 и 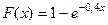при x≥0.

13. Непрерывная случайная величина X распределена по показательному закону, заданному плотностью вероятности 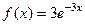при x≥0; при x<0 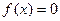. Найти вероятность того, что в результате испытания X попадёт в интервал (0,13; 0,7).

14. Диаметр круга x измерен приближённо, причём 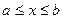. Рассматривая диаметр как случайную величину X, распределённую равномерно в интервале (a,b), найти математическое ожидание и дисперсию площади круга.

15. Математическое ожидание и среднее квадратическое отклонение нормально распределённой случайной величины X соответственно равны 10 и 2. Найти вероятность того, что в результате испытания X примет значение, заключённое в интервале (12, 14).

16. Производится измерение диаметра вала без систематических ошибок. Случайные ошибки измерения X подчинены нормальному закону со средним квадратическим отклонением σ=10 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15 мм.

17. Автомат изготавливает шарики. Шарик считается годным, если отклонение X диаметра шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая, что случайная величина X распределена нормально со средним квадратическим отклонением σ=0,4 мм, найти, сколько в среднем будет годных шариков среди ста изготовленных.

18. Непрерывная случайная величина X распределена по показательному закону, заданному при x≥0 плотностью вероятности 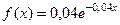; при x<0 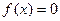. Найти вероятность того, что в результате испытания X попадёт в интервал (1, 2).

19. Найти математическое ожидание показательного распределения, заданного при x≥0: а) плотностью 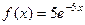; б) функцией распределения .

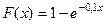20. Найти дисперсию и среднее квадратическое отклонение показательного распределения, заданного плотностью вероятности 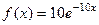(x≥0).