Задания для самостоятельного выполнения

Составить визуальные циклические алгоритмы для следующих задач.

1. Вычислить число в факториале Y=X!

2. Вычислить сумму ряда , общий член которого задан формулой An=(x*n)/n!.

3. При табулировании функции y=cos(x+a) на отрезке [1,10] c шагом h=1 определить сумму значений y , больших p.

4. Подсчитать количество цифр в целом числе Х.

5. Вычислить сумму значений функции у=x^2 на отрезке [1,5] c шагом 1.

6. * Найти минимальное значение функции Y=Sin(X)*X , на отрезке [C,D] с шагом 0.001. Реализовать цикл с постусловием.

7. Протабулировать функцию y=sin(x) на отрезке [1,5] с шагом h=0,5. Вывести предпоследнее положительное значение функции.

8. Определить постановку задачи и составить визуальный алгоритм для этой задачи, если табличное представление ее решения изображено ниже:

Условие N>0	S	N
125>0 да	0+5=5
12>0 да	5+2=7
1>0 да	7+1=8
0>0 нет

9. Составить визуальную и табличную формы алгоритма по его текстовому представлению, а также определить конечное значение S .

А) I=0; S=0; В) I=1; S=0;

ПОКА I<3 ПОКА I >1

I=I+3 S=S+1/I

S=S+I*I I=I-1

ВЫВОД S ВЫВОД S

10. Составить визуальную и текстовую форму представления алгоритма, заданного в табличной форме.

I	J	S
		0+1+2=3
		3+1+3=7
		7+2+2=11
		11+2+3=16

11. Определить является ли данный фрагмент алгоритма циклом, если да, то какого вида и какое действие является телом цикла?
12. * Протабулировать функцию Y=tg(X), при изменении X на отрезке [A,B] с шагом K и определить количество точек разрыва(M) этой функции.

13. Определите местонахождение ошибок в алгоритмическом решении следующей задачи. Найти минимальное значение функции Y=A*X²+Sin(X)*X^0,5 , для Х изменяющемся на отрезке [C,D] с шагом 0,01.

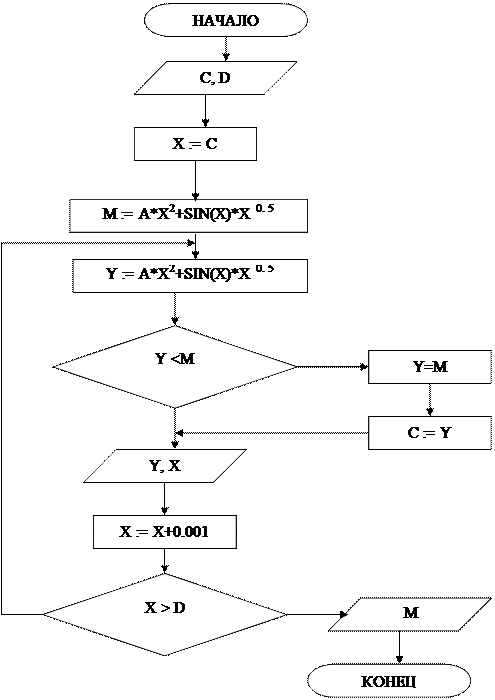8. АЛГОРИТМЫ ОБРАБОТКИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ ЧИСЕЛ

Последовательность значений - это набор однотипных величин, которые вводятся и обрабатываются циклически. Примером последовательности целых чисел может быть следующий набор значений: (2,5,-4,10,1,0). Последовательности значений отличаются от массивов значений тем, что в памяти одновременно все значения последовательности не хранятся. Для обозначения значения последовательности используют одну переменную, в которую на каждом шаге итерации вводится очередное значение последовательности. Отличительной особенностью последовательности является также возможность содержания неопределенного или неизвестного заранее количества ее значений. В этом случае критерием окончания последовательности служит некоторое особое значение, например, ноль.

Пример 7. В числовой последовательности определить сумму положительных и произведение отрицательных чисел. Решение представить с использованием циклического алгоритма с предусловием. Признак конца последовательности - значение 0.

Решение. Обозначим за Х переменную, содержащую очередное значение последовательности, за S - сумму положительных значений , за Р - произведение отрицательных значений. Полученный алгоритм приведен на рис. 14. Условие

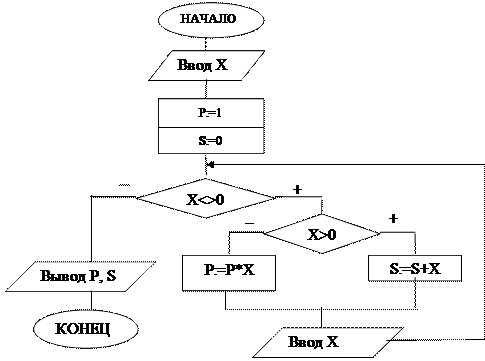Рис.14. Алгоритм вычисления суммы положительных и произведения отрицательных значений числовой последовательности

для выбора вычислений Х>0. Для вычисления суммы значений воспользуемся реккурентной формулой S=S+X с начальным значением S=0, для вычисления произведения - реккурентной формулой P=P*X с начальным значением Р=1. Условие выхода из цикла неравенство Х<>0.

Пример 8.Составить циклический алгоритм с постусловием для определения в последовательности целых чисел количества четных чисел.

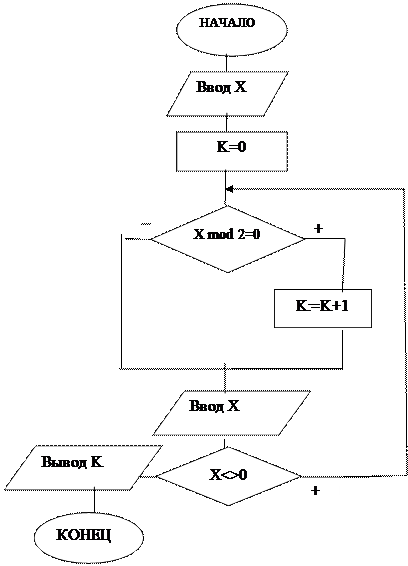Решение. Обозначим за Х переменную, содержащую очередное значение последовательности, за K - количество четных значений (рис. 15). Условие для выбора четных значений Х mod 2=0 (остаток при делении Х на 2 равен 0). Для вычисления количества значений воспользуемся реккурентной формулой К=К+1 с начальным значением К=0.

Рис. 15. Алгоритм определения количества четных чисел в последовательности значений