Естественные монополии. Максимизация прибыли естественной монополии

Естественная монополия – монополия компании, обусловленная ее уникальным положением на рынке. Естественная монополия возникает в ситуации, когда одна компания в состоянии удовлетворять весь рыночный спрос на определенные товары или услуги с более низкими средними издержками, чем это смогли бы сделать несколько более мелких компаний.

Одним из возможных способов увеличения прибыли для производителя, в той или иной мере обладающего монопольной властью, является ценовая дискриминация⁵, т.е. продажа гомогенного блага по различным ценам разным покупателям; при этом различия в ценах не связаны с затратами производства и доставки товара на рынок.

Необходимым условием осуществления ценовой дискриминации является невозможность перепродажи блага. Поэтому наиболее широкое распространение она получила в сфере услуг.

В зависимости от способа осуществления ценовой дискриминации ее делят на три категории (степени).

Дискриминацией первой степениназывается продажа каждой единицы блага по ее цене спроса. Если продавцу это удается, то кривая отраслевого спроса становится для него кривой предельного дохода. В этом случае монополия продаст такой же объем продукции, какой был бы реализован в условиях совершенной конкуренции. При этом весь потребительский излишек достается продавцу в виде добавочной прибыли.

Осуществить ценовую дискриминацию первой степени на практике удается редко. Чаще по разным ценам монополист продает не каждую единицу продукции, а определенные ее партии. Так, теплоэлектроцентраль может учесть, что минимально необходимое количество электроэнергии и тепла потребители возьмут по очень высоким ценам, а если на последующие порции своей продукции она будет снижать цены, то общий объем выручки и, возможно, прибыль возрастут. В этом суть ценовой дискриминации второй степени.

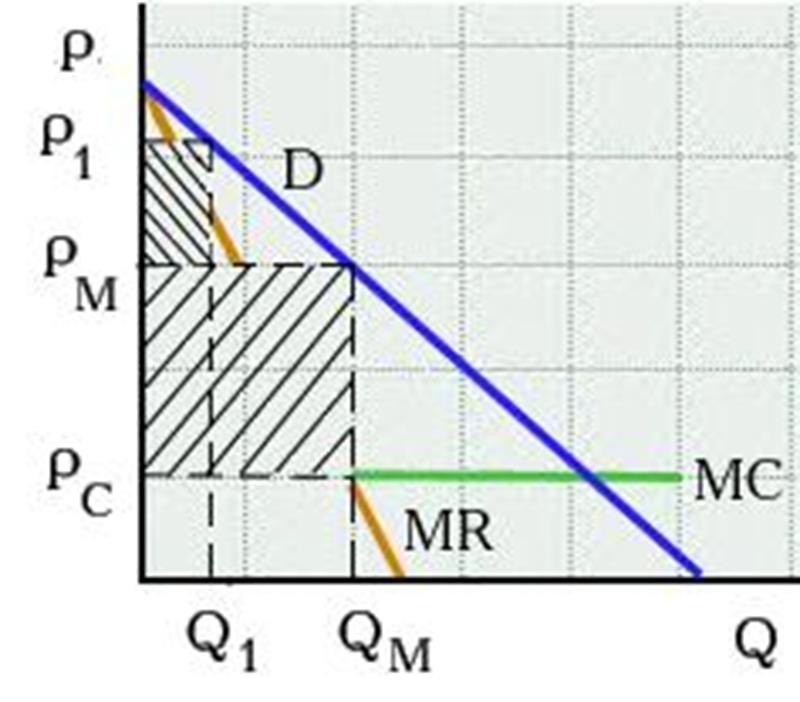
Рис. 3.1. Увеличение прибыли за счет ценовой дискриминации

При отраслевом спросе, представленном на рис. 3.1, и отсутствии ценовой дискриминации сочетание P_M,Q_M обеспечивает максимальную прибыль, равную площади нижнего заштрихованного прямоугольника. Если монополист сможет продать Q₁ ед. продукции по цене P₁, а оставшуюся партию Q_M – Q₁ по цене P_M, то его прибыль возрастет на площадь верхнего заштрихованного прямоугольника.

Рассмотрим, как следует устанавливать размер отдельных партий и их цену, чтобы прибыль при осуществлении ценовой дискриминации второй степени была максимальной. Примем в целях упрощения, что весь выпуск разбивается лишь на две партии: q₁ + q₂ = Q. При заданной функции отраслевого спроса цена на первую партию продукции есть функция от величины первой партии: P₁ = P₁(q₁), а цена на вторую партию будет зависеть как от q₁, так и от q₂: P₂ = P₂(q₁, q₂). Это связано с тем, что продажа первой партии товара укорачивает кривую спроса для второй партии: если продано q₁, то от исходной линии спроса P = g – hQ остается лишь ее часть P = g – h(Q – q₁).

Прибыль от реализации всей продукции определяется по формуле:

p = P₁(q₁)q₁ + P₂(q₁, q₂)q₂ – TC(q₁, q₂)

Условия ее максимизации:

(3.1)

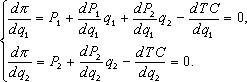
Поскольку dTC/dq₁ = dTC/dq₂ = dTC/dQ, то условие (3.1) можно представить в виде:

(3.2)

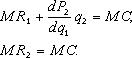
Так как P₁ и P₂ определяются по одной и той же кривой спроса, то dP₂/dq₁ = dP₂/dq₂. Учитывая также, что по определению предельной выручки MR = P + qdP/dq, и соответственно qdP/dq = MR – P, то первое условие максимизации прибыли можно записать в следующем виде: MR₁ + MR₂ – P₂ = MC. Тогда из системы уравнений (3.2) следует MR₂ = MR₁ + MR₂ – P₂ MR₁ = P₂. Таким образом, при разделении всего объема выпуска на две партии с целью их реализации по разным ценам прибыль будет максимальной, если соблюдаются следующие соотношения:

(3.3)

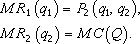
Из решения системы (3.3) находятся значения q₁ и q₂, на основе которых по функции отраслевого спроса определяются цены P₁ и P₂.

Полученный вывод можно распространить на любое число партий. Общее правило установления цен, максимизирующих прибыль при осуществлении ценовой дискриминации второй степени, таково: предельная выручка от продажи i-той партии должна равняться цене (i + 1)-й партии, а предельная выручка от продажи последней партии – предельным затратам: MR₁ = P₂; MR₂ = P₃; ...; MR_n= MC.

Ценовую дискриминацию третьейстепени можно осуществить тогда, когда отраслевой спрос предстает перед продавцом в виде отдельных групп покупателей (сегментов рынка) с различными функциями спроса. В этом случае задача монополиста установить такие цены для каждой группы покупателей, которые максимизируют общую прибыль.

Общая прибыль от продажи на n сегментах рынка определяется по формуле:

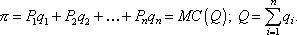
Условием ее максимизации является уравнение:

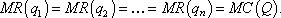
Следовательно, на каждом из сегментов рынка нужно установить такую цену, чтобы предельная выручка на всех сегментах была одинаковой и равнялась предельным затратам.

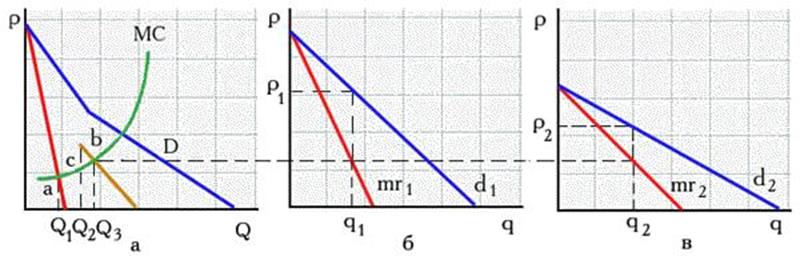
Рис. 3.2. Ценовая дискриминация 3-й степени

Графическое решение этой задачи в случае существования двух сегментов показано на рис. 3.2, а – в. Кривая отраслевого спроса D на рис. 3.2, а является ломаной линией из-за того, что на данном рынке существуют две группы покупателей с различной эластичностью спроса: D_I + D_II = D.

Если линия спроса (среднего дохода) имеет перегиб, то на линии предельного дохода возникает разрыв. В этих условиях задача нахождения цены, максимизирующей прибыль, осложняется тем, что кривая предельных затрат может пересечь кривую предельной выручки сразу в трех точках, как это имеет место на рис. 3.2 (точки a,b,c). Чтобы определить, какая из трех точек Курно соответствует максимальной прибыли, нужно сопоставить площади двух образованных пересечением MC и MR треугольников. Площадь треугольника, расположенного ниже MC, представляет убытки, возникающие при увеличении выпуска с Q₁ до Q₂, так как в этом интервале выпуска MR < MC. Площадь треугольника, расположенного выше MC, соответствует прибыли (MR > MC), образующейся при увеличении выпуска с Q₂ до Q₃. Если площадь треугольника, лежащего выше линии MC, больше площади треугольника, расположенного ниже линии MC, то максимуму прибыли соответствует точка B, так как убытки, возникающие при увеличении выпуска в интервале Q₁,Q₂, с лихвой компенсируются прибылью, образующейся при расширении выпуска с Q₂ до Q₃. Когда площадь треугольника, расположенного над кривой MC, меньше площади треугольника, находящегося под ней, тогда максимуму прибыли соответствует точка A.

Из проведенного анализа следует, что никогда не нужно выбирать среднюю из трех точек пересечения линии MC с разорванной линией MR , а из двух крайних точек максимальной прибыли соответствует та, которая принадлежит треугольнику с большей площадью.

Проекция оптимальной точки Курно на линии предельных доходов каждого из сегментов рынка указывает на те сочетания Pi , Qi , которые обеспечивают получение максимальной прибыли.

Проведение ценовой дискриминации позволяет сохранить на рынке потребителей с низкой покупательной способностью.