Физический и геометрический смысл производных гравитационного потенциала

Гравитационное поле Земли относится к классу потенциальных полей, т. е. таких, когда каждой точке пространства вокруг Земли (вне притягиваемых масс) можно по­ставить в соответствие некоторую непрерывную и имеющую непрерывные производ­ные функцию. Производные этой функции по направлениям, кроме того, равняются проекциям силы тяжести на эти направления. Такую функцию называют гравитаци­онным потенциалом W. Чтобы эта функция удовлетворяла определению потенциала принимают следующей:

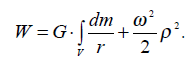(2.8)

Из определения потенциала вытекает, что

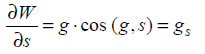(2.9)

Следовательно, математически введенное понятие потенциала приобретает физи­ческую сущность, так как приращение потенциала dW - это работа по перемещению материальной точки на расстояние ds. При перемещении точки в направлении, перпен­дикулярном к направлению силы тяжести, cos (g, s) =0 и dW=0. После интегрирования получаем

W = const. (2.10)

Так как W является функцией координат х, у и r, полученное равенство есть уравнение некоторой поверхности, обладающей следующим свойством: в любой ее точке сила тяжести направлена перпендикулярно к ней. Такая поверхность называется уровенной или эквипотенциальной поверхностью. Различные значения const в урав­нении (2.10) соответствуют различным уровенным поверхностям. Уровенную поверх­ность, совпадающую со свободной невозмущенной поверхностью воды земных океа­нов, называют геоидом. Геоид по форме очень близок к эллипсоиду вращения с весьма малым (1/297 — 1/298,8) коэффициентом сжатия. Представляя форму Земли в виде эл­липсоида вращения малого сжатия, по теореме Клеро определяют теоретическое, нор­мальное значение ускорения силы тяжести γ_o, которое в зависимости от широты на­блюдения ф принято выражать формулой

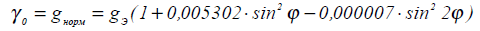(2.11)

гдеg_э — среднее значение поля на экваторе Земли.

Это выражение позволяет рассчитать γ_o на поверхности геоида для любой точки наблюдения с известной широтой в предположении однородности внутреннего строе­ния Земли и отсутствия какого-либо нарушения идеальной (сферической) формы по­верхности Земли.

Из выражения (2.9) следует, что производная потенциала по отвесной линии есть полная составляющая силы тяжести:

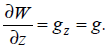(2.12)

Если выбрать прямоугольную систему координат, при которой ось Z направлена вертикально вниз, а ось Х по меридиану, то, дифференцируя выражение (2.12) по на­правлениям х, у и z, получаем

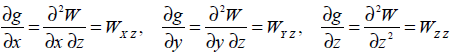(2.13)

Этими формулами определяются скорости изменения или градиенты g вдоль оп­ределенных направлений х, у и z (физический смысл производных). Существуют также и другие вторые производные по­тенциала:

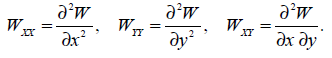(2.14)

С помощью вторых производных (2.14) можно установить форму уровенной по­верхности (геоида), изучаемой в геодезической гравиметрии (физический смысл).

Размерность вторых производных потенциала силы тяжести определяется отношением приращения силы тяжести к расстоянию, т. е. [м-с ^-2 *м ^-1 ]=[с ^-2 ]. В качестве практической единицы измерения вторых производных в гравиразведке принята величина 10 ^-9 с ^-2 , получившая название этвеша (Э) и соответствующая изменению силы тяжести 0,1-10 ^-5 м*с ^-2 или 0,1 мГал на 1 км. Для усредненных параметров Земли в зави­симости от широты точки наблюдения по специальным формулам рассчитывают нор­мальные значения вторых производных потенциала силы тяжести.