Аналитическое продолжение аномалий

235 стрсеркеров

Значения потенциала и его производных, известные в некоторой области, не занятой возмущающими массами, могут быть найдены в области более широкой и, в том числе, внутри возмущающих масс, если там эти (потенциал и производные) функции сохраняют свою гармоничность (т.е. кроме особых точек или областей, где они теряют гармоничность).

Изучение пространственного распределения производных потенциала вне возмущающих масс и в окрестности особых точек позволяет получить ценные сведения для интерпретации аномалий.

Рассмотрим принципы аналитического продолжения – на примере продолжения в верхнее полупространство.

Пусть ось Z направлена вверх, Q1 и Q2 – две бесконечные плоскости, перпендикулярные оси Z.

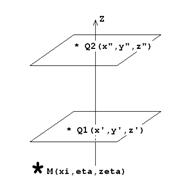
На одной из них (на плоскости Q1) зададим некую функцию U(x,y,z). Ни сама плоскость Q1 , ни все пространство вверх от нее не должны содержать особых точек.

Для двухмерных возмущающих тел можно записать (на плоскости Q1 – для прямой Q1(x’,z’)):

,

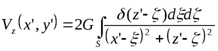а для прямой Q2(x”,z”) на плоскости Q2 :

.

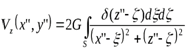Их спектры, соответственно (так же, как и при выводе формулы (a)):

,

.

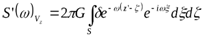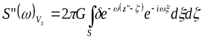Поделив их одно на другое, получаем:

.

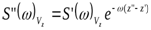Здесь 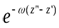–частотная характеристика аналитического продолжения функции 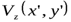с уровня z’ на уровень z”.

Можно и наоборот: 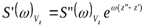– с соответствующей характеристикой аналитического продолжения: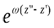

Учитывая полученные частотные характеристики, можно на основе теоремы о свертке (об интеграле свертки)1 получить следующее окончательное выражение:

.

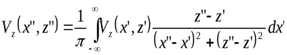Это – интеграл Пуассона для перехода (пересчета поля) на верхний уровень.

Билет № 14

1.Гравитационный потенциал объекта с однородной плотностью?

Ответ:Все планеты Солнечной системы имеют сферическую форму. Поэтому имеет смысл определить гравитационный потенциал шара. Для упрощения задачи, мы будем предполагать, что плотность шара зависит только от расстояния до его центра Нетрудно убедиться, что такой шар притягивает точно так же, как и материальная точка с массой равной массе шара и помещенная в его центр. Чтобы в этом убедиться, необходимо для формулы (

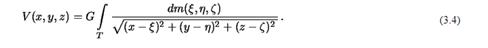выбрать такую систему координат, с помощью которой было бы удобно выполнять интегрирование.

Для начала, представим себе, что точка 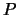находится вне шара. Соединим эту точку с центром шара (точка О), полученный радиус-вектор обозначим через 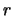. Радиус-вектор элемента массы 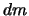будем обозначать буквой 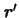. Следовательно расстояние между элементом массы и точкой 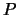, которое мы обозначили греческой буквой 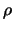, будет иметь вид

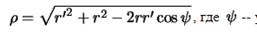
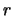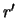угол с вершиной в центре шара, образованный радиус-векторами и . Наконец, элемент массы 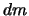определяется произведением плотности на объем элементарно малого параллелепипеда со сторонам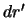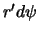и , , и 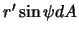. Здесь мы ввели еще одну степень свободы -- поворот вокруг оси 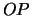на угол 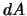. Таким образом,

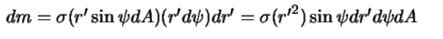
Теперь вместо формулы (3.4) записать

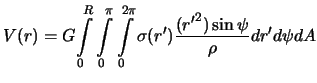(3.5)

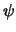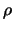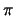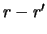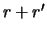Заменим переменную интегрирования на . Определим пределы интегрирования. Очевидно, что вместо 0 и нужно взять и , а 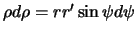. Переменную 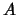подынтегральное выражение не содержит, поэтому внутренний интеграл легко берется. Вместо (3.5) теперь будем иметь

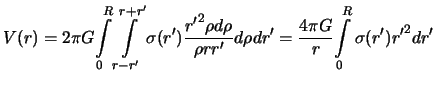Нетрудно догадаться, что 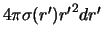есть масса бесконечно тонкой сферы 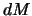, поэтому

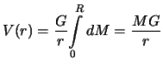(3.7)

Таким образом, мы пришли к очень важному выводу: шар со сферически симметрично распределенной массой притягивает так же, как и материальная точка с массой равной массе шара и помещенной в его центре.