Разделение горных пород на два класса

1. Элементы теории распознавания образов.

Пусть проверяется гипотеза о том, что статистическая совокупность распределена по закону 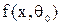, т. е. 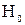: 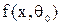, при конкурирующей гипотезе, состоящей в том, что статистическая совокупность распределена по закону ,

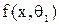т. е. .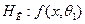

f(x)

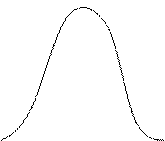
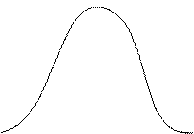
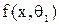
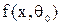
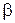
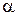
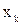X

Рис. 4.1

Наша задача состоит в том, чтобы по наблюдаемому признаку х установить, какая из гипотез верна.

Построение критерия начнем с выбора такого множества на оси Ох, что если х будет принимать значения из этого множества, то мы будем делать вывод о том, что верна нулевая гипотеза 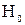. Это множество мы будем называть множеством принятия нулевой гипотезы: 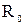. Дополнительное множество будем называть критическим множеством или множеством отклонения нулевой гипотезы: .

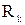Пусть нам известна критическая точка 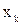, тогда если наблюдаемый признак будет 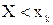, то будем делать вывод, что верна нулевая гипотеза ,

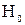если 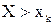, тогда делаем вывод, что верна альтернативная гипотеза .

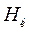1) Пусть 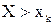, следовательно мы принимаем альтернативную гипотезу 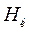, в то время как на самом деле может быть верна гипотеза 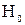. При этом мы совершаем ошибку.

Определение 4.1

Ошибкой первого рода называется

ошибка, которая состоит в том, что мы

отвергаем нулевую гипотезу, в то время как она верна.

Ошибка первого рода называется уровнем значимости и обозначается .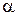

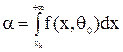
В общем виде:

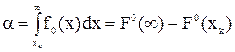(4.1)

Если x распределен по нормальному закону распределения с математическим ожиданием 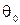и среднеквадратическим отклонением :

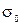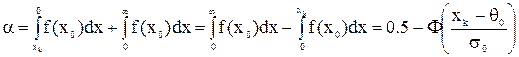
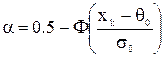(4.2)

2) Пусть 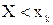, мы делаем вывод, что верна 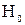в то время, как она на самом деле не верна. При этом мы совершаем ошибку.

Определение 4.2

Ошибкой второго рода называется cобытие, состоящее в том, что мы принимаем нулевую гипотезу в то время, как на самом деле она не верна.

В общем виде:

(4.3)

Если х распределен по нормальному закону, и извесны его математическое ожидание и среднеквадратическое отклонение , то

(4.4)

Определение 4.3

(1 – β) называется мощностью крите-

рия.

2. Разделение горных пород на два класса

В геологической практике при поисках и разведке полезных ископаемых постоянно возникает задача классификации объектов на два класса. Это может быть разделение объектов на рудные и безрудные, выделение одной горной породы на фоне другой, выделение геохимических аномалий, связанных с определенными геологическими явлениями среди других геохимических аномалий.

Во всех случаях мы сталкиваемся с задачей разделения объектов на два класса по изучаемому признаку.

Обычно задача классификации состоит из двух этапов.

На первом этапе (этапе обучения) по выборкам из имеющихся двух классов на эталонных объектах, определяется решающее правило, а также ошибки и надежность классификации.

На втором этапе классифицируют уже неизвестные объекты по изучаемому признаку, т.е относят их к тому или иному классу в соответствии с выработанным критерием.

Итак, пусть имеется два класса горных пород, в которых изучается какое-либо свойство. И пусть взяты выборки из каждого класса

R1

f2(x)

x

xk

β

α

R2

f1(x)

f(x)

на этапе обучения. В результате анализа данных двух выборок построены эмпирические функции плотности распределения каждого класса.

Рис 4.1

При проведении геологических работ необходимо по измеряемому параметру Х отнести образцы горной породы к одному, либо к другому классу.

Таким образом, выдвигаются две гипотезы:

Гипотеза H₁ - образец горной породы относится к I классу.

Гипотеза H₂ - образец горной породы относится ко 2 классу.

Будем полагать, что нам известны априорные (известные до опыта) вероятности встречи горной породы в районе (вероятности гипотез) P(H1) и P(H₂).

P(H₁)+P(H₂)=1

При выборе x_k, т.е. при разделении пространства признака Х на два (R₁ и R₂) необходимо учитывать, с чем сопряжено совершение ошибок 1 и 2 рода.

Пусть С₁₂- стоимость ошибки первого рода,

С₂₁- стоимость ошибки второго рода,

С₁₁ и С₂₂ - стоимости правильных решений.

Вероятности правильных решений вычисляются по формулам:

;

Тогда средняя стоимость, которую приходится платить при многократном распознавании неизвестных объектов, равна сумме стоимостей неправильных и правильных решений с учетом вероятностей их появлений и априорных вероятностей.

(4.4)

Определение 4.4

Отношение плотностей вероятностей называется коэффициентом правдоподобия.

Если С₁₁ = С₂₂ = 0, т.е. если нет затрат на правильное решение,

С₁₂ = С₁, а С₂₁ = С₂, отношение правдоподобия равно:

(4.5)

При одинаковых стоимостях ошибок С₁ = С₂ .

Критерий Кательникова

Если же априорные вероятности равны P(H₁) = P(H₂) = 0.5, то

Критерий максимального правдоподобия

Следовательно, в этом случае x_k есть абсцисса точки пересечения дифференциальных функций распределения f₁(x) и f₂(x).

1. Область R₁ состоит из значений х, для которых <1, при этом x < x_k.

2. Область R₂ состоит из значений х, для которых >1, при этом х > x_k.

Определение 4.5

Стратегия решений, при которой критическая точка выбирается так, что минимизирует средний риск (средняя стоимость) называется стратегией Байеса.

Рассмотрим пример разделения горных пород на два класса по изучаемому признаку.

Пусть в некотором районе имеются два класса пегматитов - рудные и безрудные. На хорошо геологически изученных участках из каждого класса пегматитов взяты выборки, в которых изучено какое-либо свойство Х. Полученные данные обработаны: для каждой выборки определены эмпирические функции распределения и функции плотности распределения. Результаты обработки сведены в таблицы.

1 класс.

	ni	Wi	Vi	Fi
8-10		0,02	0,01	0,02
10-12		0,04	0,02	0,06
12-14		0,28	0,14	0,34
14-16		0,36	0,18	0,70
16-18		0,20	0,10	0,90
18-20		0,06	0,03	0,96
20-22		0,04	0,02	1,00

2 класс

	ni	Wi	Vi	Fi
8,2-9,4		0,04	0,033	0,04
9,4-10,6		0,18	0,150	0,22
10,6		0,32	0,267	0,54
11,8-13,0		0,28	0,233	0,82
13,0-14,2		0,16	0,133	0,98
14,2-15,4		0,02	0,017	1,00

	xk

V2

V2

a

b

β=0,13

b

a

V2

x

Fэ

α=0,24

Vi

x

Vi

Рис.4.2

По полученным данным требуется установить решающее правило (критерий разделения пород на два класса по изучаемому признаку) и оценить ошибки диагностики при массовом распознавании образцов пегматитов. Фактически, изучив свойство Х образца, взятого из исследуемого пегматитового тела, следует отнести его к классу рудных пегматитов или к классу безрудных.

Решающее правило будем строить исходя из стратегии Байеса. При равных априорных вероятностях гипотез P(H₁) = P(H₂) = 0,5 критическая точка х_k выбирается как абсцисса точки пересечения эмпирических кривых функции плотности распределения. Рис.1.3.5. Следовательно, если исследуемый образец характеризуется свойством х < x_k, его следует отнести к 1 классу, если х > x_k - ко второму.

При массовом распознавании мы будем совершать ошибки. Ошибка первого рода , а ошибка второго рода . Эти ошибки могут быть определены по графикам эмпирических функций распределения. В рассмотренном примере х_k = 13,3; .Общая ошибка диагностики

g = 0,5×0.13+0.5 × 0.24 = 0.185

Вопросы к четвёртой лабораторной работе.

1.В чём смысл работы?

2. В чём суть стратегии Байеса?

3. Дать определения ошибок первого и второго рода, написать формулы и показать на графике.

4. Написать формулы для критерия Котельникова и критерия максимального правдоподобия.

Лабораторная работа №5.