Вычисление точечных оценок параметров распределения.
Пусть из генеральной совокупности извлечена выборка объёмом N образцов и в этой выборке изучается свойство X. Естественно возникает задача определить основные параметры этой совокупности.
Параметрами распределения являются:
Математическое ожидание, дисперсия, среднеквадратическое отклонение и другие начальные и центральные моменты.
Естественно, что истинное математическое ожидание, дисперсию, среднеквадратическое отклонение генеральной совокупности изучить невозможно, т.к. её объём может достигать очень больших размеров. Поэтому вычисляют оценки по выборочным данным.
Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определённым требованиям.
Определение 2.1
Оценка называется несмещённой, если её математическое ожидание равно оцениваемому параметру.
Например, пусть дана генеральная совокупность X, для которой известно математическое ожидание M(X)=a. Из этой генеральной совокупности извлечена выборка объёма N и для этой выборки найдена оценка математического ожидания q1. Повторим опыт, т.е. извлечём из генеральной совокупности другую выборку того же объёма и по её данным найдём оценку q2. Повторяя опыт многократно, получим числа q1, q2,...,qn неравные между собой. Тогда, если математическое ожидание M[q] равно оцениваемому параметру a (M[q]=a), то оценка будет несмещённой.
Однако несмещённая оценка не всегда даёт хорошее приближение. Действительно, возможные значения q могут быть сильно рассеяны вокруг своего среднего значения, т.е. дисперсия оценки D[q] может быть значительной. В этом случае найденная по данным одной выборки оценка может оказаться весьма удалённой от своего среднего значения, а значит и от оцениваемого параметра тоже. По этой причине к статистической оценке предъявляется требование эффективности.
Определение 2.2
Оценка называется эффективной, если она имеет наименьшую дисперсию.
При рассмотрении выборок большого объёма к статистической оценке предъявляется требование состоятельности.
Определение 2.3
Оценка называется состоятельной, если она стремится по вероятности к оцениваемому параметру при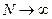 
.
Оценками математического ожидания являются:
выборочная средняя, мода и медиана.
Определение 2.4
Выборочной средней называют среднее арифметическое значение признака выборочной совокупности:
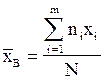(2.1),
где:
n- количество интервалов группирования,
xi -середина интервала группирования,
ni- частота попадания в интервал группирования,
N - объём выборки.
Выборочная средняя есть несмещённая, эффективная и состоятельная оценка математического ожидания.
Определение 2.5
 |
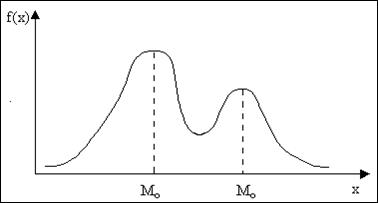Мода (M0) это абсцисса экстремума эмпирической дифференциальной функции распределения.
Определение 2.6:
 |
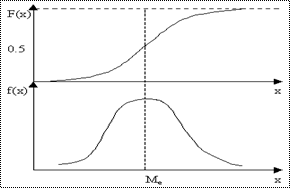Медиана (Me) это абсцисса линии, которая делит площадь ограниченную дифференциальной функцией на две равные части.
 |
Оценками дисперсии являются:выборочная дисперсия и квадрат стандарта.
Определение 2.7
Выборочной дисперсией называют среднее арифметическое квадратов отклонений наблюдаемого значения признака от своего выборочного:
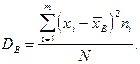(2.2)
Выборочная дисперсия является смещённой оценкой дисперсии, несмещённой оценкой дисперсии является квадрат стандарта:
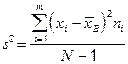. (2.3)
Оценкой среднеквадратического отклонения является стандарт s .
Для оценки отклонения эмпирического распределения от нормального используют различные характеристики, в том числе асимметрию и эксцесс.
Определение 2.8
Асимметрией называется оценка центрального момента третьего порядка, делённая на s3.
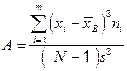. (2.4)
Она характеризует различия в крутизне
склонов графика эмпирической дифференциальной функции распределения.
 |
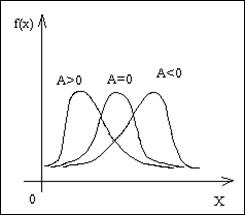Если X распределён по нормальному закону, асимметрия A=0. Если A>0, тогда правая ветвь дифференциальной функции пологая, а левая ветвь крутая. Если A<0, тогда правая ветвь дифференциальной функции крутая, а левая ветвь пологая.
Определение2.9
Эксцессом называется оценка центрального момента четвёртого порядка, делённая на s4 и минус 3.
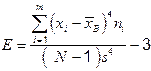. (2.5)
Она характеризует различия в крутизне
вершины графика эмпирической дифференциальной функции распределения.
 |
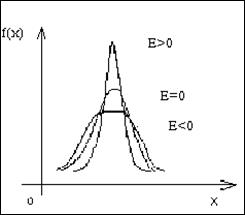Если X распределён по нормальному закону, тогда E=0.
Рассмотрим сквозной пример.
Пусть дана генеральная совокупность, из которой извлечена выборка объёмом N=50:
15.1 18.7 14.3 16.1 12.8 14.7 19.1 15.5 13.5 15.5
16.7 11.2 13.4 12.4 14.7 17.2 13.612.7 13.7 17.3
15.2 12.2 16.2 14.9 15.6 14.1 20.6 14.9 13.2 14.2
16.4 18.3 17.4 12.3 16.9 17.8 12.8 21.8 14.8 17.7
9.1 14.6 13.8 10.8 13.1 12.1 15.7 15.4 14.7 15.6
Для этой выборки известны
xi -середины интервалов группирования,
ni- частота попадания в интервал группирования (см. §1).
Найдём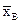 
, s2, A, E.
Решение:
Найдём выборочную среднюю.
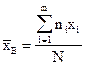
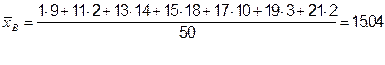
Заполним таблицу:
| xi | xi- 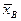 =t | t2 | t3 | t4 | ni |
| -6.04 | 36.48 | -220.34 | 1330.97 | ||
| -4.04 | 16.32 | -65.93 | 266.35 | ||
| -2.04 | 4.16 | -8,49 | 17,32 | ||
| 0.04 | 0.0016 | 0.000064 | 0.00000256 | ||
| 1.96 | 3.84 | 7.53 | 14.76 | ||
| 3.96 | 15.68 | 62.09 | 245.91 | ||
| 5.9 | 34.81 | 205.38 | 1211.74 |
Вычислим квадрат стандарта.
.
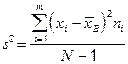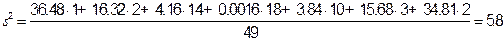
Стандарт равен: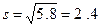 
Вычислим асимметрию.
.
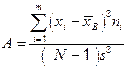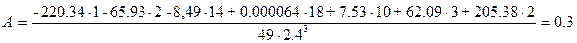
Вычислим эксцесс.
.
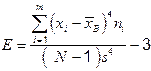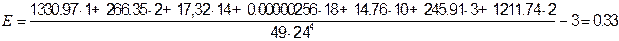
Вопросы ко второй лабораторной работе.
1. В чём смысл работы?
2. Какие параметры распределения Вы знаете?
3. Какие оценки параметров распределения Вы знаете?
5. Написать формулы для второй лабораторной работы и сказать, что они характеризуют.
6. Дать определения характера оценок из второй лабораторной работы.
7. Показать на графике оценки математического ожидания.
Лабораторная работа №3.