Индексы качественных показателей.

Наряду с индексами физического объема продукции широко применяются индексы качественных показателей. Качественный показатель характеризует уровень изучаемого результативного показателя в расчете на количественную единицу и определяется как отношение данного результативного показателя к связанному с ним количественному показателю, на единицу которого он определяется.

Формулы индексов качественных показателей рассмотрим на примере расчета индексов цен.

Индивидуальный индекс цен:

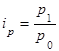(15) Для характеристики изменения цен на товары применяют два индекса: с весами базисного или отчетного периодов:

Iр = 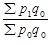- индекс Ласпейреса; (16)

Iр = 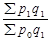- индекс Пааше (17)

Рассчитанный по формуле (17) индекс цен Паше показывает, во сколько раз увеличился (уменьшился) в среднем уровень цен на товар, который реализован в текущем периоде, или сколько процентов составляет его рост (уменьшение) в текущем периоде по сравнению с базисным периодом.

Разность числителя и знаменателя индекса (17) - ∆_p = (∑ p₁ q₁ - ∑ p₀ q₁) соответствует абсолютной экономии (∆_p< 0) или абсолютномe перерасходу (∆_p> 0) денежных средств покупателей в результате изменения цен на эти товары.

Индекс Ласпейреса показывает влияние изменения цен на стоимость количества товаров, которые реализованы в базисном периоде.

Таким образом, индексы цен Пааше и Ласпейреса на идентичны и для одинаковых исходных данных не совпадают, так как имеют разное экономическое содержание: индекс Ласпейреса используют в прогнозировании объема товарооборота в связи с вероятными изменениями цен на товары в будущем периоде, а индекс Пааше применяют при изучении отчетных данных, когда целью анализа является качественная оценка изменения товарооборота в результате изменения цен в отчетном периоде.

Агрегатный индекс Пааше после преобразования принимает форму среднегармонического индекса:

Iр = 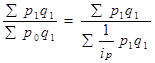(18)

Индекс Ласперейса принимает форму средней арифметической взвешенной:

Iр = 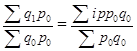(19)

В этих индексах:

ip – индивидуальные индексы цен;

р1q1 – стоимость товаров по видам в отчетном периоде;

р0q0 - стоимость товаров по видам в базисном периоде.

Таким образом, преобразованные выше агрегатные индексы представляют собой средневзвешенные величины из индивидуальных индексов, весами для которых служат стоимости товаров.

Широкое применение в статистике получил индексный метод анализа динамики средних величин. Средние, как известно, вычисляются для однородных единиц совокупности.

Индекс характеризующий изменение средних значений (уровней) индексируемых величин называют индексом переменного состава:

Iр = 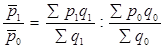(20)

Этот индекс характеризует изменение средневзвешенной цены за счет изменения самой цены и объема продажи товаров.

Для выявления влияния каждого из факторов на динамику средней цены товара исчисляют индекс цен постоянного состава (или фиксированного состава) и индекс структурных сдвигов.

Индекс цен постоянного состава равен:

Iр = 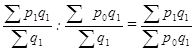(21)

Он характеризует изменение средней цены единицы товара за счет изменения только цены по каждому рынку. Этот индекс иначе называют индексом цен в постоянной структуре. Динамика средней цены за счет изменения в составе количества проданных товаров на отдельных рынках определяется с помощью индекса структурных сдвигов:

Iстр = 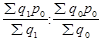(22)

Индекс структурных сдвигов может быть получен иначе - с помощью взаимосвязи индексов: делением индекса переменного состава на индекс постоянного состава:

Iстр = ( 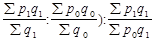или (23)

I стр = Iр : Iр (24)

После преобразования формулы получим индекс структурных сдвигов иного вида:

I стр = 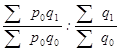(25)