Э л е к т р о м а г н и т н ы е я в л е н и я
Методические указания
к выполнению лабораторных работ
для студентов всех специальностей
Йошкар-Ола
Составители: Л.А.Григорьев, В.П.Медведчиков, Т.И.Краева,
Г.Ю.Кожинова, А.С.Шилова, А.С.Масленников,
Л.П.Алимбек
УДК 531 / 076.5 / : 378
ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ: Методические указания к выполнению лабораторных работ для студентов всех специальностей / Сост. Л.А.Григорьев, В.П.Медведчиков, Т.И.Краева и др.: Под ред. Л.А.Григорьева. - Йошкар-Ола: МарГТУ, 2001. - 56 с.
Приведены лабораторные работы по разделу "Магнетизм" курса общей физики. Каждая работа содержит краткое теоретическое описание изучаемого явления, описание установки, порядок выполнения работы и обработки результатов измерений, вопросы самопроверки.
Рис. 33. Табл. 3. Библиогр.: 4 назв.
Печатается по решению редакционно-издательского совета МарГТУ
Рецензент - Ю.Б.Грунин, доктор химических наук, профессор МарГТУ
© Марийский государственный
технический университет, 2000
ВВЕДЕНИЕ
Методические указания включают в себя восемь работ из лабораторного практикума по разделу "Магнетизм" и соответствуют учебному плану.
При выполнении работ в лаборатории магнетизма студенты
изучают физические явления: возникновение магнитного поля в пространстве, окружающем проводники с током, движение электронов в электромагнитном поле, намагничивание и перемагничивание ферромагнетиков, явление электромагнитной индукции и самоиндукции, эффект Холла, прохождение квазистационарного тока через цепи, содержащие R, C, L - элементы и изменение амплитуды напряжения в этих цепях, резонанс напряжений, возникновение стоячих волн в струне;
изучают физические законы: Био-Савара-Лапласа, полного тока, Фарадея, Ома для цепи переменного тока;
овладевают методами расчета магнитных полей, основанными на законах Био-Савара-Лапласа и полного тока;
исследуют зависимость магнитной индукции в веществе и магнитной проницаемости ферромагнетика от напряженности внешнего магнитного поля, индуктивности катушки от магнитной проницаемости среды, амплитуды вынужденных колебаний от частоты, скорости распространения поперечных колебаний в струне от ее натяжения;
овладевают методами измерения величины индукции магнитного поля, магнитной проницаемости, коэрцитивной силы, остаточной индукции, коэффициента самоиндукции катушки индуктивности, удельного заряда электрона, амплитудных и эффективных значений тока и напряжения в RCL-цепях, скорости распространения поперечных колебаний вдоль струны и др.;
приобретают навыки работы с приборами: генератором напряжения звуковых частот, осциллографом, амперметрами постоянного и переменного тока, цифровыми вольтметрами, автотрансформатором и др.
Руководство к выполнению каждой лабораторной работы включает в себя краткое теоретическое описание физического явления, описание установки, порядок выполнения работы и обработку результатов измерений.
Методические указания предназначены для студентов 1 - 2 курсов всех специальностей.
МАГНИТНОЕ ПОЛЕ
Индукция магнитного поля 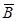 есть вектор, с которым связана та часть силы, действующая на движущийся заряд, которая пропорциональна его скорости v. Полная сила, действующая на заряд q в произвольной точке М, равна
есть вектор, с которым связана та часть силы, действующая на движущийся заряд, которая пропорциональна его скорости v. Полная сила, действующая на заряд q в произвольной точке М, равна
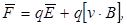 (1)
(1)
где 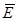 - напряженность электрического поля, а
- напряженность электрического поля, а 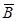 - вектор, для определения которого выражение (1) можно считать исходным.
- вектор, для определения которого выражение (1) можно считать исходным.
Чтобы определить индукцию B в данной точке М, необходимо:
1) Измерить силу, действующую в точке М на неподвижный заряд q. Это даст нам кулоновскую силу 
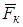 и напряженность электрического поля
и напряженность электрического поля 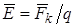
2) Измерить силу F, действующую на заряд q в момент прохождения его через точку М с заданной скоростью v, и вычесть из нее кулоновскую силу Fк. Полученную разность сил называют силой Лоренца:
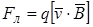 (2)
(2)
3) Повторить эту операцию для всевозможных направлений скорости 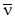 при постоянной величине
при постоянной величине 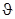 и найти
и найти 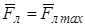 (в этом случае искомый вектор
(в этом случае искомый вектор 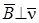 ). Тогда В = Fлmax /(q
). Тогда В = Fлmax /(q 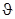 ), а направление
), а направление 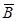 определяется так, как
определяется так, как
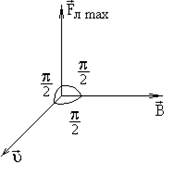 Рис.1 Рис.1 | показано на рис.1. Из конца вектора B поворот вектора 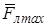 к к 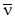 по кратчайшему расстоянию виден совершающимся против хода часовой стрелки. Единицей измерения магнитной индукции является тесла (Тл): 1 Тл = 1 Н/(1 АЧ1 м). Опыт показывает, что определенный таким образом вектор B дает правильное значение силы Лоренца по кратчайшему расстоянию виден совершающимся против хода часовой стрелки. Единицей измерения магнитной индукции является тесла (Тл): 1 Тл = 1 Н/(1 АЧ1 м). Опыт показывает, что определенный таким образом вектор B дает правильное значение силы Лоренца 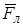 при любой скорости заряда. при любой скорости заряда. |
Одним из источников магнитного поля являются движущиеся заряды и, в частности, проводники с током. Согласно закону Био-Савара-Лапласа элемент провода 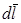 с током I создает в произвольной точке М (рис.2.) магнитное поле с
с током I создает в произвольной точке М (рис.2.) магнитное поле с
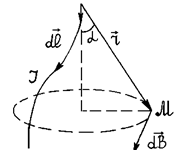 Рис.2 Рис.2 | магнитной индукцией 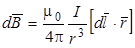 , (3) где μo - магнитная постоянная; , (3) где μo - магнитная постоянная; 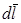 - вектор, направление которого совпадает с направлением тока; - вектор, направление которого совпадает с направлением тока; 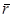 - вектор, проведенный от элемента - вектор, проведенный от элемента 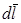 в точку М. Для нахождения магнитного поля B, создаваемого в точке М всем проводом, необходимо в точку М. Для нахождения магнитного поля B, создаваемого в точке М всем проводом, необходимо |
провести суммирование (интегрирование) по всей длине провода. В качестве примера рассмотрим магнитное поле на оси z кругового тока (рис.3).Оси х и у
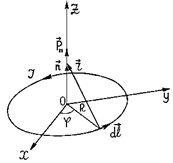 Рис.3 Рис.3 | выберем так, как показано на рис.3.При этом для векторов dl и r получим: 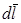 = Rdφ {-sinφ, cosφ, 0}, (4) = Rdφ {-sinφ, cosφ, 0}, (4) 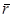 = {-Rcosφ, -Rsinφ, z}. (5) Подставляя выражения (4) и (5) в формулу (3) и интегрируя по φ от φ1= О до φ2= 2π, получим для проекций вектора B в точках оси z следующие значения: = {-Rcosφ, -Rsinφ, z}. (5) Подставляя выражения (4) и (5) в формулу (3) и интегрируя по φ от φ1= О до φ2= 2π, получим для проекций вектора B в точках оси z следующие значения: |
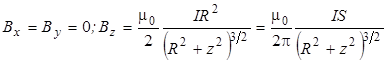 , (6)
, (6)
где S = pR2 - площадь, ограниченная контуром с током.
Величину
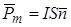 , (7)
, (7)
где 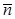 - нормаль к площади S, связанная с направлением тока в контуре правилом правого винта, называют магнитным моментом контура. Магнитное поле витка с током в любой точке пространства пропорционально Рm и определенным образом связано с направлением
- нормаль к площади S, связанная с направлением тока в контуре правилом правого винта, называют магнитным моментом контура. Магнитное поле витка с током в любой точке пространства пропорционально Рm и определенным образом связано с направлением 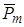
В частности, формулу (6) можно записать в виде
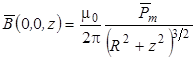 . (8)
. (8)
Движение заряженной частицы с зарядом e по замкнутой траектории эквивалентно круговому току I = eυ, где υ - частота обращения частицы по орбите. При этом величина орбитального магнитного момента частицы равна
Рm = eυS, (9)
где S - площадь, ограниченная замкнутой траекторией частицы. Кроме орбитального магнитного момента, микрочастицы могут иметь еще собственный (спиновый) магнитный момент (см. лабораторную работу 5). Следовательно, микрочастицы (например, электрон) являются источниками магнитного поля B даже и в том случае, если бы их скорость равнялась нулю. Интересно, что спиновый магнитный момент могут иметь и нейтральные частицы (например, нейтрон). Таким образом, магнитное поле B порождается как движущимися зарядами, так и спиновыми магнитными моментами микрочастиц.
1. ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ СОЛЕНОИДА
Цель работы: экспериментальное изучение распределения магнитного поля вдоль оси соленоида.
Приборы и принадлежности: соленоид, измеритель магнитной индукции Ш1-8, источник тока.
1.1 Теоретические сведения
Соленоид представляет собой тонкий провод, плотно навитый, виток к витку, на цилиндрический каркас. В отношении создаваемого им магнитного поля соленоид эквивалентен системе одинаковых круговых токов с общей прямой осью. Сначала рассмотрим один виток. Оси х, у и z выберем так, как показано на рис.1.1. Согласно формуле (6) для проекции вектора B в точках оси z имеем:
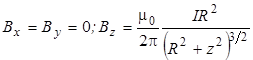 , (6)
, (6)
причем Вz > О во всех точках оси z. Направление В на оси витка с током определяется правилом правого винта: если головка винта вращается "вслед" за током в витке, то направление движения острия винта совпадает с направлением магнитного поля B на оси витка.
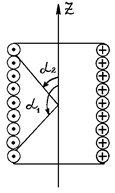 Рис. 1.1 Рис. 1.1 | Рассмотрим теперь соленоид (см.рис.1.1). Очевидно, на оси соленоида вектор В направлен вдоль оси z, также как и в случае одного витка, ибо все витки создают в каждой точке оси магнитное поле одного направления. Суммирование полей всех витков приводит к следующему выражению для индукции В в произвольной точке О оси соленоида: 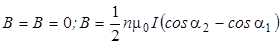 (1.2) (1.2) |
где n - число витков на 1 м длины соленоида, I - сила тока в про- воде, α1 и α2 - углы между осью и прямыми, проведенными из точки О к нижнему (z = z1) и верхнему (z = z2) витку соответственно (z1< z2). В частности, при z1= - ∞ , z2= +∞ (бесконечно длинный соленоид)
В = μonI, (1.3)
а при z1= -∞, z2= 0 или при z1= 0, z2= +∞(то есть на краю полу- бесконечного соленоида)
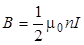 , (1.4)
, (1.4)
Практически формулы (1.3) и (1.4) используются вместо выражения (1.2), если длина соленоида во много раз превышает его диаметр.
Схема установки приведена на рабочем месте. Для экспериментального определения поля на оси соленоида в данной работе используется измеритель магнитной индукции ИМИ Ш-1-8, принцип действия которого основан на эффекте Холла.
Эффект Холла заключается в возникновении поперечного электрического поля и разности потенциалов в металле или в полупроводнике, по которому проходит электрический ток, при помещении его в магнитное поле, перпендикулярное направлению тока. Если в магнитное поле помещен металл или полупроводник с электронной проводимостью, то электроны, движущиеся со скоростью v в магнитном поле B, под действием силы Лоренца Fл = - e [v∙B] (см. формулу (2)) отклоняются в определенную сторону (в данном случае вверх - см. рис.1.2,а), что показывает появление отрицательных зарядов на одной грани образца и соответственно недостаток их, т.е. появление положительных зарядов, на другой грани. В полупроводнике с дырочной проводимостью знаки зарядов на указанных гранях (см. рис.1.2,б) обратные.
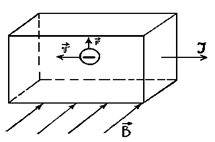 а) а) | 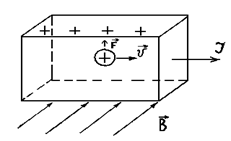 б) б) |
| Рис. 1.2 |
Возникшее поперечное электрическое поле препятствует отклонению носителей заряда в магнитном поле. Разность потенциалов при эффекте Холла равна 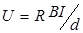 , где R – постоянная Холла, зависящая от свойств полупроводника и температуры, В – магнитная индукция, I – сила тока в образце, d – линейный размер образца в направлении вектора B. Таким образом, измеряя Холловскую разность потенциалов, возникшую в данном полупроводнике при заданных условиях, можно найти величину магнитной индукции:
, где R – постоянная Холла, зависящая от свойств полупроводника и температуры, В – магнитная индукция, I – сила тока в образце, d – линейный размер образца в направлении вектора B. Таким образом, измеряя Холловскую разность потенциалов, возникшую в данном полупроводнике при заданных условиях, можно найти величину магнитной индукции: 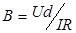
Поскольку при заданных R, d, I магнитная индукция пропорциональна разности потенциалов, то прибор, измеряющий разность потенциалов, можно проградуировать в единицах магнитной индукции.
Датчик Холла имеет размеры 1,5х1х0,2 мм и помещается в нужную точку оси соленоида с помощью зонда "С". При этом плоскость датчика перпендикулярна к оси зонда (и к оси соленоида).
1.2. Порядок выполнения работы
А. Подготовка к проведению измерений:
1) Включить прибор в сеть.
2) Установить тумблер "СЕТЬ" на передней панели прибора Ш1-8 в верхнее положение, при этом должна загореться сигнальная лампочка. Прогреть прибор в течение 15 минут.
3) Шкалу первой декады отсчетного устройства "ОТСЧЕТ ИНДУКЦИИ, Т" установить в положение О.
4) Тумблер "ПОЛЯРНОСТЬ" установить в положение "N".
5) Тумблер "ИНДИКАТОР" установить в положение "ТОЧНО".
6) Резисторами "УСТ.НУЛЯ" - "ГРУБО", "ТОЧНО" совместить стрелку индикатора с отметкой "О" шкалы. При этом следует расположить зонд так, чтобы датчик Холла был максимально удален от источников магнитного поля. (Поскольку в данной работе измеряется индукция поля в соленоиде, а зонд "С" находится внутри его, важно, чтобы в момент установки нуля ток в соленоиде отсутствовал).
Б. Проведение измерений:
1) Включить в сеть цепь соленоида.
2) Регулятором на верхней панели установки задать определенное значение тока соленоида I, величина которого контролируется с помощью амперметра. При этом в окружающем пространстве, в том числе и в месте расположения зонда, появится магнитное поле. Стрелка индикатора на передней панели прибора Ш1-8 должна отклониться. Если стрелка отклоняется вправо, то следует изменить направление тока в соленоиде тумблером "Т" блока питания.
3) Для определения величины индукции магнитного поля установить тумблер "ИНДИКАТОР" в положение "ГРУБО", шкалу первой декады от- счетного устройства "ОТСЧЕТ ИНДУКЦИИ, Т" перевести в положение "О,О". При помощи остальных ручек "ОТСЧЕТ ИНДУКЦИИ, Т" добиться совмещения стрелки индикатора с нулем путем постепенного увеличения показаний шкал отсчетного устройства в следующем порядке: сна- чала на всех декадах выставить нули (на первой декаде - "О,О"); поворачивая переключатель второй декады на одно деление назад, аналогичные действия выполнить с переключателями третьей и четвертой декад. При этом стрелка индикатора установится на нуль, а искомое значение магнитной индукции берется по отсчетному устройству "ОТСЧЕТ ИНДУКЦИИ, Т".
1.3. Задание и отчетность
Задание 1. Построить график зависимости величины индукции магнитного поля от положения зонда на оси соленоида.
1) Установить определенное значение тока в соленоиде (не превышающее 0,7 А).
2) С помощью измерителя магнитной индукции ИМИ Ш1-8 измерить численное значение В в различных точках оси соленоида, перемещая зонд "С" от одного из концов соленоида к другому через каждые 2 см. Данные измерений занести в таблицу.
3) Повторить указанные в п.2 измерения для обратного направления тока в соленоиде, для чего переключатель на передней панели перевести в положение 2. При этом необходимо также перевести тумблер "ПОЛЯРНОСТЬ" прибора Ш1-8 в положение "S" и провести операцию установки нуля.
4) Построить график зависимости В = f(l), взяв в качестве В среднее из двух измерений при различных направлениях тока.
5) Зная число витков на единицу длины соленоида и силу тока в соленоиде, по формулам (1.3), (1.4) рассчитать В в средней и крайней точках длинного соленоида. Оценить погрешность измерений. Сопоставить полученные результаты с результатами прямых измерений.
Задание 2. Построить график зависимости магнитной индукции от силы тока в соленоиде.
1) Установить зонд в средней точке соленоида.
2) Изменяя силу тока в соленоиде от 1 А до нуля через 0,1 А, измерить индукцию магнитного поля при каждом значении I.
3) Построить график зависимости В = f(I) и объяснить полученные результаты.
1.4. Дополнительное задание
1) Провести измерения В на оси соленоида при наличии в нем полого ферромагнитного сердечника.
2) Провести измерения В в центре соленоида при наличии в нем полых сердечников из парамагнитного и диамагнитного вещества. Объяснить полученные результаты.
1.5. Контрольные вопросы
1. Как определяется индукция магнитного поля B? Единицы измерения В.
2. Сформулируйте закон Био-Савара-Лапласа.
3. Вывести формулу, описывающую магнитное поле прямолинейного проводника с током, поле витка с током, поле соленоида.
4. Что такое поток магнитной индукции, потокосцепление?
5. В чем заключается эффект Холла? Как используется это явление в данной работе?
6. Объясните результаты проведенных измерений.
Литература. [1, §§ 15,4, 15,5, 18,1, 18,2; 2, §§ 33, 36; 3, §§ 42, 43, 50].
2. ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ МАГНИТНОГО ПОЛЯ ЗЕМЛИ С ПОМОЩЬЮ ТАНГЕНС-БУССОЛИ.
Цель работы: определение горизонтальной составляющей вектора магнитной индукции магнитного поля Земли для данного места.
Приборы и принадлежности: источник питания, потенциометр, ключ, миллиамперметр, тангенс-буссоль.
2.1. Теоретические сведения
Земля представляет собой естественный магнит, полюса которого не совпадают с ее географическими полюсами (рис.2.1). Южный магнитный полюс S находится примерно в 450 км от северного полюса C, а северный магнитный N - в 450 км от южного географического Ю.
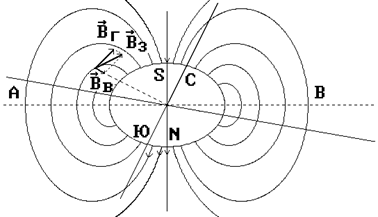 Рис.2.1 Рис.2.1 | Магнитный экватор Географический экватор |
Географические полюса Земли - точки на ее поверхности, через которые проходит прямая (ось), вокруг которой Земля совершает суточное вращение.
Магнитные полюса Земли - точки, в которых магнитное поле перпендикулярно поверхности Земли.
Магнитные меридианы - это линии больших кругов, проведенные через магнитные полюса Земли, а вертикальная плоскость, проходящая через магнитный меридиан, называется плоскостью магнитного меридиана.
В точках магнитного экватора А и В магнитное поле 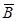 параллельно поверхности Земли, а у магнитных полюсов S и N - вертикально. Во всех остальных точках (над поверхностью Земли) магнитное поле
параллельно поверхности Земли, а у магнитных полюсов S и N - вертикально. Во всех остальных точках (над поверхностью Земли) магнитное поле 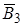 можно представить в виде суммы двух взаимоперпендикулярных векторов
можно представить в виде суммы двух взаимоперпендикулярных векторов 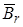 и
и 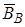 , где
, где 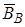 перпендикулярен к поверхности Земли, а
перпендикулярен к поверхности Земли, а 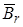 направлен вдоль поверхности.
направлен вдоль поверхности.
Соответственно 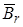 называют горизонтальной, а
называют горизонтальной, а 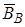 – вертикальной составляющей магнитного поля Земли. Если в данной точке Земли свободно подвесить магнитную стрелку, т.е. подвесить ее за центр масс так, чтобы она могла поворачиваться и в горизонтальной, и в вертикальной плоскостях, то она установится по направлению магнитного поля В в данной точке.
– вертикальной составляющей магнитного поля Земли. Если в данной точке Земли свободно подвесить магнитную стрелку, т.е. подвесить ее за центр масс так, чтобы она могла поворачиваться и в горизонтальной, и в вертикальной плоскостях, то она установится по направлению магнитного поля В в данной точке.
Отметим, что 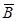 – это индукция магнитного поля, именно эту величину мы имеем в виду, когда говорим о магнитном поле. Иногда говорят о напряженности магнитного поля
– это индукция магнитного поля, именно эту величину мы имеем в виду, когда говорим о магнитном поле. Иногда говорят о напряженности магнитного поля 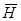 . В вакууме
. В вакууме
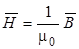 , (2.1)
, (2.1)
где μo - магнитная постоянная (μo = 4π∙10-7 Гн/м).
Однако в веществе 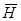 и
и 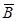 не всегда совпадают по направлению
не всегда совпадают по направлению
( 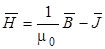 , где
, где 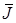 - намагниченность вещества).
- намагниченность вещества).
Магнитная стрелка устанавливается в определенном направлении под действием 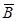 , а не
, а не 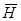 . На магнитную стрелку, помещенную в однородное поле, действует момент сил
. На магнитную стрелку, помещенную в однородное поле, действует момент сил 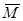 , равный векторному произведению вектора магнитного момента магнитной стрелки
, равный векторному произведению вектора магнитного момента магнитной стрелки 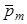 и вектора магнитной индукции поля
и вектора магнитной индукции поля 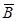 .
.
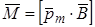 . (2.2)
. (2.2)
Модуль момента равен M = pm B sinα, где α - угол между векторами 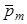 и
и 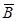 .
.
Если магнитную стрелку закрепить на вертикальной оси, то она повернется в горизонтальной плоскости под действием горизонтальной составляющей 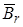 и установится вдоль
и установится вдоль 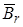 .
.
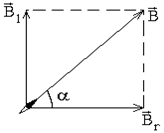 Рис.2.2 Рис.2.2 | С помощью кругового тока около стрелки (компаса) можно создать еще одно горизонтальное магнитное поле 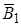 и тогда стрелка установится уже вдоль направления и тогда стрелка установится уже вдоль направления 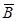 равнодействующей обоих магнитных полей (рис.2.2). Удобнее всего выбрать направление равнодействующей обоих магнитных полей (рис.2.2). Удобнее всего выбрать направление 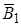 , перпендикулярное к , перпендикулярное к 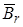 |
2.2. Описание установки
В данной работе определение горизонтальной составляющей магнитного поля Земли производится с помощью прибора, называемого ТАНГЕНС-БУССОЛЬЮ (ТБ). Это короткая катушка большого радиуса (по сравнению с размером стрелки компаса), на которую намотано определенное число витков изолированного провода. Практически проволока намотана в виде кругового жгута небольшой толщины, который помещен в трубку из немагнитного материала. В центре катушки помещена на острие небольшая магнитная стрелка (при этом можно считать, что она находится в однородном поле).
На рис.2.3 изображено сечение катушки горизонтальной плоскостью. 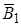 - вектор магнитной индукции поля, созданного круговым током,
- вектор магнитной индукции поля, созданного круговым током, 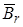 - горизонтальная, а
- горизонтальная, а 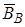 - вертикальная составляющие магнитного поля Земли.
- вертикальная составляющие магнитного поля Земли.
При прохождении тока по витку в его центре возникает магнитное поле, которое направлено перпендикулярно к плоскости витка:
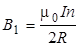 (2.3)
(2.3)
где I -сила тока, n -число витков, R -радиус витка буссоли. Расчет проводится по закону Био-Савара-Лапласа.
Если плоскость витка (буссоли) установить вертикально и так, чтобы продольная ось магнитной стрелки лежала в этой же плоскости (плоскости магнитного меридиана), то горизонтальная составляющая
Плоскость магнитного
меридиана (вертикальная)
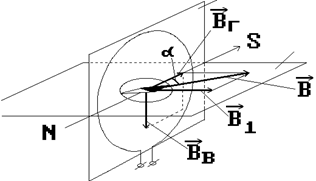 Рис.2.3 Рис.2.3 | Горизонтальная плоскость |
магнитного поля Земли Вг и поле кругового тока В1 в центре буссоли окажутся перпендикулярными друг другу. Стрелка установится по направлению равнодействующей В, т.е. по диагонали прямоугольника, сторонами которого являются вектор магнитного поля кругового тока В1 и вектор магнитной индукции горизонтальной составляющей поля Земли Вг.
Тогда
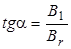 и
и 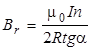 (2.4)
(2.4)
2.3. Порядок выполнения работы
1) Собрать (если не собрана) схему (см.рис.2.4). БП - блок питания.
2) Установить тангенс-буссоль в плоскости магнитного меридиана Земли ( по магнитной стрелке).
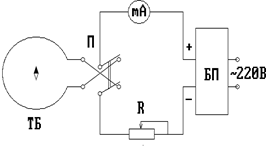 Рис.2.4 Рис.2.4 | 3) Замкнуть переключатель П и установить определенный ток (I1= 10 mA) с помощью потенциометра R. Зафиксировать угол поворота магнитной стрелки α1. 4) Не меняя величины тока, переключателем П изменить направление тока в буссоли и, |
записать новое отклонение стрелки α2 – (перемена направления тока позволяет избавиться от ошибки возникающей от неточного совпадения плоскости буссоли с плоскостью магнитного меридиана). Для расчета
берется α = (α1 + α2)/2.
5) Такие же измерения провести при 4 других значениях тока (20, 30, 40, 50 mA).
6) Построить график зависимости tgα от токаI (рис.2.5).
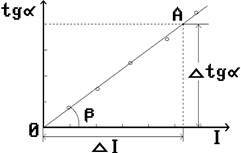 Рис.2.5 Рис.2.5 | 7) Из графика определить j постоянную тангенс-буссоли (постоянную для данного места Земли и для данного прибора величину): С = сtgb = DI/Dtga. (2.5) 8) Рассчитать магнитную индукцию горизонтальной составляющей поля Земли Вг по формуле |
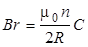 (2.6)
(2.6)
где n -количество витков и R -средний радиус витка катушки, (данные установки см. на панели тангенс-буссоли: n = витков, R = м).
8) Все наблюдения и результаты вычислений записать в табл. 1
9) Оценить погрешность измерений.
10) Сравнить полученный результат с табличным значением величины горизонтальной составляющей Вг магнитной индукции поля Земли: Вг= 20 мкТл.
2.4. Результаты измерений
Таблица 1
| Опыты | I (mA) | α1 | α2 | α | tgα | C=ctgβ | Br (мкТл) |
2.5. Контрольные вопросы
1. В каких единицах измеряется индукция магнитного поля?
2. Сформулируйте и запишите закон Био-Савара-Лапласа.
3. На чем обосновано утверждение, что свободно подвешенная магнитная стрелка определяет направление вектора индукции магнитного поля?
4. Как направлены горизонтальная и вертикальная составляющие магнитного поля Земли? На рис.8 покажите индукцию ВЗ магнитного поля Земли.
5. Как и почему магнитная стрелка ориентируется в магнитном поле?
6. Как узнать направление тока в витках по отклонению стрелки?
7. Почему магнитная стрелка должна быть малых размеров?
8. Получите выражение для магнитного поля В на оси кругового тока из закона Био-Савара-Лапласа.
Литература. [1, §§ 21.1, 21.2, 21.3, 22.2; 3, §§ 39, 41, 48; 4, §§ 109, 110]
3. ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА МЕТОДОМ ФОКУСИРОВКИ ПУЧКА ЭЛЕКТРОНОВ В ПРОДОЛЬНОМ МАГНИТНОМ ПОЛЕ.
Цель работы: определение отношения e/m, где е - величина заряд электрона, а m - его масса.
Приборы и принадлежности: электронно-лучевая трубка, соленоид, осциллограф, блок питания.
3.1. Теоретические сведения
При движении в магнитном поле на электрон действует сила Лоренца (рис.3.1):
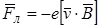 , (3.1)
, (3.1)
где -е - заряд электрона (e > 0), v - скорость электрона, B - индукция магнитного поля.
Таким образом, Fл = -еvB sina, где a - угол между векторами 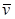 и
и 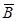 , а направление
, а направление 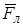 выбирается так, как показано на рис.3.1 (вспомните определение векторного произведения).
выбирается так, как показано на рис.3.1 (вспомните определение векторного произведения).
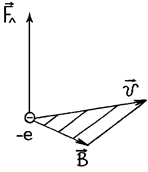 Рис.3.1 Рис.3.1 | Если 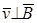 , то электрон движется в фиксированной плоскости, перпендикулярной к , то электрон движется в фиксированной плоскости, перпендикулярной к 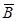 , т.к. , т.к. 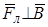 , и ускорение электрона вдоль , и ускорение электрона вдоль 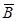 равно нулю. равно нулю. 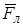 не совершает работу над электроном (так как не совершает работу над электроном (так как 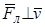 ) и изменяет скорость ) и изменяет скорость 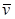 только по направлению. При этом нормальное ускорение электрона остается постоянным по величине и равно только по направлению. При этом нормальное ускорение электрона остается постоянным по величине и равно 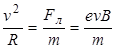 , (3.2) , (3.2) |
откуда радиус окружности, по которой движется электрон, равен
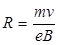 , (3.3)
, (3.3)
Один оборот электрон совершает за время
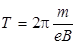 , (3.4)
, (3.4)
Таким образом, период обращения электрона по окружности не зависит от скорости электрона. Период определяется только величиной индукции 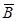 и удельным зарядом электрона.
и удельным зарядом электрона.
Если угол a между векторами скорости 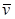 и индукции
и индукции 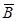 не равен p/2, то скорость
не равен p/2, то скорость 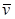 можно представить в виде суммы:
можно представить в виде суммы: 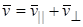 , где
, где 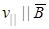 , а
, а 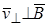 . При этом
. При этом 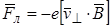 , так как
, так как 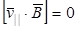 .
.
Таким образом, электрон движется с постоянной скоростью 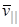 вдоль
вдоль 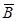 и одновременно вращается вокруг линии, параллельной
и одновременно вращается вокруг линии, параллельной 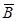 , с периодом,
, с периодом,
 Рис.3.2 Рис.3.2 | определенным по формуле (3.4). В результате траектория электрона является винтовой линией (рис.3.2), проекция которой на плоскость, перпендикулярную к B, представляет собой окружность радиуса 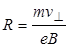 |
Предположим, что в однородном магнитном поле В из некоторой точки С вылетают электроны (пучок электронов), имеющие одинаковую скорость 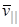 и разные скорости
и разные скорости 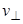 . Если
. Если 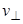 «
« 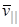 для всех электронов (малые углы α, см.рис.3.3), то
для всех электронов (малые углы α, см.рис.3.3), то 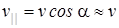 . В этом случае все электроны, вылетающие из точки С, через одинаковое время Т попадут в одну и ту же точку О или, как говорят, сфокусируются в точке О. Очевидно, что
. В этом случае все электроны, вылетающие из точки С, через одинаковое время Т попадут в одну и ту же точку О или, как говорят, сфокусируются в точке О. Очевидно, что
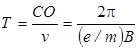
Следовательно, зная расстояние СО, v и В, можно найти е/m. На этой идее и основан метод определения удельного заряда электрона в дан- ной работе. На рис.3.3 схематически показана электронно-лучевая трубка. Электроны, испускаемые горячим катодом, проходят через отверстие в диафрагме А, играющей роль анода.
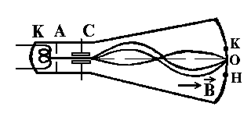 Рис.3.3 Рис.3.3 | При ускоряющей разности потенциалов Uа = jа - jк электроны приобретают скорость, которую можно определить из соотношения: ½mv2 = eU (3.5) Затем пучок электронов проходит между пластинами конденсатора С, на которые пода- |
ется переменное напряжение. Под действием переменного электрического поля электроны в разные моменты времени будут отклоняться на разные углы α от оси прибора и на экране трубки появится светящаяся полоска НК (см. рис.3.3).
Кроме электрического поля на электрон будет действовать продольное магнитное поле соленоида, внутрь которого вставлена электронно-лучевая трубка. Таким образом, в промежутке между диафрагмой и экраном электроны будут двигаться по винтовым линиям.
При увеличении магнитного поля линия НК на экране осциллографа сокращается и постепенно стягивается в точку. Эту точку называют фокусом электронов. Обозначим через Вф магнитное поле, при котором наступает фокусировка. За время Т электроны проходят отрезок
L = v||Т. (3.6)
Учитывая, что v|| ≈ v при малых α выражение (3.4) в формулу (3.6) получим:
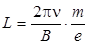 (3.7)
(3.7)
Таким образом, все электроны через время, равное одному периоду, пересекут ось прибора на одинаковом расстоянии L от конденсатора. На рис.3.3 показаны траектории нескольких электронов. Все они пересекаются в одной точке О.
Магнитное поле можно подобрать так, чтобы фокус пришелся как раз на флуоресцирующий экран. При этом отрезок L равен расстоянию между конденсатором и экраном, которое легко измерить.
Подставляя в формулу (3.7) значение скорости из выражения (3.5), получаем расчетную формулу для удельного заряда электрона:
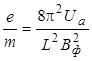 (3.8)
(3.8)
В данной установке используется электронный осциллограф СИ-1, электронно-лучевая трубка которого вынута из него и закреплена в соленоиде, создающем магнитное поле. Оси трубки и соленоида совпадают. Питание трубки и напряжение, подаваемое на отклоняющие пластины, подводятся многожильным кабелем. Анодное напряжение трубки измеряется электростатическим киловольтметром.
3.2. Порядок выполнения работы
1) Собрать схему (имеется на рабочем месте установки. При этом ручки осциллографа установить в положение: "Род синхронизации" - на "Внешнее, "Делитель" - на "Калибровку", "Род работы" - на "Усиление".
2) Включить блок питания осциллографа. После прогрева на экране трубки должна появиться светящаяся линия. Отрегулировать яркость и четкость линии ручками "Яркость" и "Фокус". Расположить светящуюся линию в центре экрана электронно-лучевой трубки ручками "Смещение У" и "Смещение Х".
3) С помощью ручек осциллографа "Усиление" и "Калибровка" ограничить длину светящейся линии до 1..1,5 см, чтобы угол α был мал.
4) Измерить величину ускоряющего напряжения Ua с помощью вольтметра блока питания. Величину Ua записать в таблицу измерения.
5) Включить блок питания соленоида тумблером "Сеть". Перед включением ручка "Регулировка тока соленоида" должна находиться в положении "О".
6) Постепенно увеличивая силу тока в соленоиде, добиться, чтобы светящаяся линия на экране трубки стянулась в точку при данной величине ускоряющего потенциала. При дальнейшем увеличении силы тока на экране вновь появится светящаяся линия, которая затем снова стянется в точку. Второе прохождение через фокус происходит в том случае, когда электроны на пути к экрану совершают два оборота по винтовой линии, третье прохождение - при трех оборотах и т.д. Каждое прохождение электронов фиксируется и значение тока соленоида Iсn / n (n - число прохождения электронов через фокус), соответствующее этим прохождениям, заносится в таблицу измерений.
7) На движение электронов в трубке влияют внешние поля. Наибольшее влияние на точность измерений оказывает продольное магнитное поле, складывающееся с полем соленоида. Внешнее продольное поле накладывается на поле соленоида. Для того, чтобы исключить влияние внешних полей, измерения, указанные в п.6 проводятся при двух направлениях тока в соленоиде. Это выполняется с помощью тумблера "Переполюсовка соленоида".
Полученные значения I+сn при прямом включении соленоида и I-cn при обратном включении соленоида нужно усреднить для каждого прохождения электронов через фокус и среднее значение занести в таблицу измерений. Соответствующие значения Вфп найти по графику В= f(I).
Если Вф1, Вф2, Вф3 - магнитные поля, при которых электроны фокусируются на экране после прохождения одного, двух и трех витков по спирали соответственно, то нужно найти среднее значение
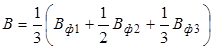 ,
,
которое и подставляется затем в формулу (3.8) для определения е/m.
Абсолютная ошибка в определении e/m находится по формуле
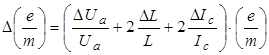
где учтено, что ∆Вф/Вф = ∆Iс/Iс.
Таблица 2
| m | I+сn, A | I-cn, A | Icn, A | Вфп, Тл | Ua, B | L, м | e/m, Кл/к2 | ∆(e/m), Кл/к2 |
3.4. Контрольные вопросы
1. Сила Лоренца.
2. По какой траектории движется электрон в однородном магнитном поле при произвольном направлении начальной скорости?
3. В чем заключается фокусировка электронов?
4. Каким будет движение электронов в электронно-лучевой трубке при переменном напряжении на отклоняющих пластинах при В = О и В ≠ О?
5. Как изменяется скорость электронов при движении в постоянном магнитном поле?
6. Чему равен период обращения электрона в магнитном поле?
7. Получите расчетная формула для определения е/m.
Литература. [1, §§ 18.1, 18.3; 2, §§ 36-38; 3, §§ 41, 43] .
4. ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА
МЕТОДОМ МАГНЕТРОНА
Цель работы: знакомство с методом магнетрона и определение удельного заряда электрона (е/m).
Приборы и принадлежности: электронная лампа 2Ц2С (или аналогичная ей), соленоид, источник питания, вольтметр, амперметр, миллиамперметр.
4.1. Теоретические сведения
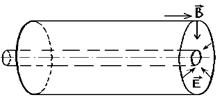 Рис.4.1 Рис.4.1 | Катод и анод лампы, используемой в данной работе, выполнены в виде соосных цилиндрических поверхностей (рис.4.1). Катод нагревается нитью накала и испускает электроны. При анодном напряжении электри-ческое поле Е между электродами направлено |
по радиальным прямым от анода к катоду и на электроны действует кулоновская сила
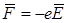 , (4.1)
, (4.1)
направленная от катода к аноду (-е - заряд электрона).
При значениях Ua ~ 10 В, которые используются в данной работе, начальная скорость электрона vк мала по сравнению с va и ею можно пренебречь. При этом кинетическую энергию электрона, падающего на анод, можно вычислить по формуле
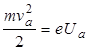 , (4.2)
, (4.2)
где m - масса электрона, va - скорость электрона вблизи анода. Отсюда
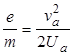 , (4.3)
, (4.3)
Таким образом, для нахождения е/m достаточно (при заданном Ua) знать va. С этой целью лампу помещают внутрь соленоида, представляющего собой тонкий провод, плотно навитый, виток к витку , на цилиндрический каркас. Оси лампы и соленоида совпадают. Если по соленоиду идет ток Iс, то магнитное поле внутри него направлено параллельно оси соленоида (см. рис.4.1) и равно
В = μμonIc, (4.4)
где μ - магнитная проницаемость среды (для воздуха μ = 1),
μo - магнитная постоянная, n - плотность витков в соленоиде.
Получаемая в данном случае конфигурация E и B напоминает конфигурацию скрещенных полей в магнетронах-генераторах электромагнитных колебаний в области сверхвысоких частот. Отсюда и название метода.
Рассмотрим характер движения электронов в лампе. При B = О электроны движутся от катода к аноду по радиальным прямым. При B ≠ О на электроны действует сила Лоренца (см.рис.3.1 и формулу (3.1)). 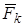 и
и 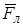 перпендикулярны к оси системы, поэтому каждый электрон движется в фиксированной плоскости, перпендикулярной к этой оси. Сила Лоренца
перпендикулярны к оси системы, поэтому каждый электрон движется в фиксированной плоскости, перпендикулярной к этой оси. Сила Лоренца 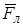 перпендикулярна и к
перпендикулярна и к 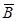 и к
и к 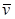 . Она изменяет лишь направление
. Она изменяет лишь направление 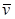 , не совершая работы над электроном. Поэтому энергия электрона, достигшего анода, определяется той же формулой (4.2).
, не совершая работы над электроном. Поэтому энергия электрона, достигшего анода, определяется той же формулой (4.2).
Пусть, например, электрон достигает анода в точке М (рис.4.2). Обозначим через α угол между радиальной прямой ОМ и скоростью va.
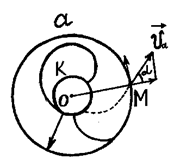 Рис.4.2 Рис.4.2 | Угол α зависит от величины B. В частности, при В = О угол α = О. При определенной (критической) величине магнитного поля (В = Вкр) угол α= π/2. При В > Вкр электроны, пройдя вблизи анода, начнут вновь приближаться к катоду. При этом анодный ток Ia резко уменьшится. Для того, чтобы это произошло, необходимо, чтобы в точке М радиус кривизны траектории электрона r не превышал радиус анода ra (по крайней мере). Радиус кривизны траектории |
входит в выражение для нормального ускорения:
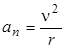 .
.
Так как α = π/2, то силы 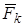 и
и 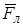 в точке М направлены по линии ОМ в разные стороны. Поэтому должно выполняться условие
в точке М направлены по линии ОМ в разные стороны. Поэтому должно выполняться условие
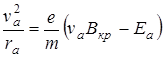 , откуда
, откуда
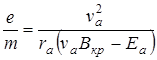 . (4.5)
. (4.5)
где Еa - напряженность электрического поля вблизи анода.
Сравнивая выражения (4.3) и (4.5), получаем:
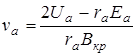 (4.6)
(4.6)
В данном случае 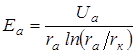 (формула для E в цилиндрическом конденсаторе).
(формула для E в цилиндрическом конденсаторе).
Учитывая это, а также зависимость (4.4), и подставляя выражение (4.6) в формулу (4.3), получим:
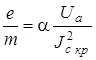 , где
, где 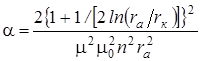
Расчеты, проведенные выше, относились к случаю, когда длина цилиндрических электродов лампы во много раз превышает их диаметры, а длина соленоида во много раз больше диаметра одного витка. В лабораторной установке эти условия выполняются лишь приближенно. Однако и в этом случае точный расчет дает такую же зависимость удельного заряда электрона от Uа и Iс кр. Изменится лишь коэффициент α. Величина α указана на установке.
4.3. Описание установки и метода измерений
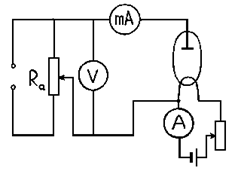
Для определения удельного заряда электрона используется двух- электродная лампа, включенная по схеме, данной на рис. 4.3.а.
Лампа помещена в центральную часть соленоида, схема включения которого приведена на рис.4.3.б. Ток в цепи соленоида устанавливают с помощью реостата Rс.
 а) а) | 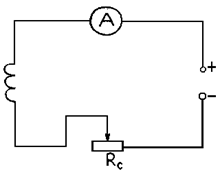 б) б) |
| Рис.4.3 |
Реостатом Ra поддерживается постоянное анодное напряжение Uа. Анодный ток измеряется миллиамперметром mA. Для определения критического тока Iс кр снимают график зависимости анодного тока Ia от тока в соленоиде Iс, экспериментальные кривые Ia = Ia (Ic) не будут делать вертикаль-
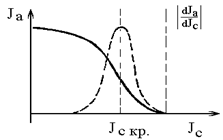 Рис.4.4 Рис.4.4 | ного сброса силы анодного тока при определенном значении Ic (риc.4.4), что объясняется разбросом в начальных скоростях электронов, покидающих катод. Для определения Ic кр нужно провести графическое дифференцирование полученных кривых. Ic кр соответствует максимуму на графике зависи- |
мости 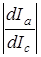 от Ic (эта зависимость показана пунктиром на рис.4.4). Вместо графического дифференцирования можно ограничиться нахождением точки на графике Iа = Iа (Iс), в которой касательная имеет максимальный наклон (это делается с помощью линейки). Соответствующее значение Ic и будет критическим.
от Ic (эта зависимость показана пунктиром на рис.4.4). Вместо графического дифференцирования можно ограничиться нахождением точки на графике Iа = Iа (Iс), в которой касательная имеет максимальный наклон (это делается с помощью линейки). Соответствующее значение Ic и будет критическим.
4.4. Выполнение работы и обработка результатов
1) Включить схему, собранную согласно рис.4.3, в сеть 220 В.
2) После 3 минут прогрева катода установить одно из рекомендованных значений анодного напряжения Uа.
3) Увеличивая ток в цепи соленоида ступенями по 0,1 А. Записать для каждого значения силы тока соленоида Ic соответствующее значение анодного тока Iа. При этом анодное напряжение следует поддерживать постоянным.
4) Опыт повторить для трех анодных напряжений (указывает преподаватель).
5) По результатам опыта для каждого Uа на миллиметровой бумаге построить график зависимости анодного тока от тока в соленоиде (на одном рисунке).
6) Из графиков найти критический ток Iс кр в соленоиде для каждого значения Uа, затем по формуле (4.7) вычислить е/m. Из трех значений для е/m взять среднее арифметическое.
7) Оценить погрешность вычислений.
8) Используя табличные данные для заряда и массы электрона, рассчитать величину удельного заряда электрона. Сравнить с экспериментально полученной величиной е/m.
4.5. Контрольные вопросы
1. Что называют удельным зарядом электрона?
2. Какие силы действуют на электрон при его движении между электродами лампы? Чему они равны и как направлены?
3. По какой траектории движется электрон при наличии Е и В.
4. Что такое критическое поле Вкр и критический ток Ic кр?
5. Как определяется е/m электрона в данной работе?
6. Почему спад на кривой зависимости Iа от Iс получается не в виде ступеньки, а размытым?
Литература. [1, §§18.1; 2, §§ 37; 3, §§ 72-74].
5. ИЗУЧЕНИЕ ФИЗИЧЕСКИХ СВОЙСТВ ФЕРРОМАГНЕТИКОВ
Цель работы: изучение зависимости магнитной индукции B в веществе от напряженности H внешнего магнитного поля. Определение зависимости магнитной проницаемости m от напряженности магнитного поля Н. Определение коэрцитивной силы и остаточной индукции.
Приборы и принадлежности: ферритовый тороид, осциллограф, генератор синусоидальных сигналов, цифровой вольтметр, амперметр, резисторы, конденсатор.
5.1. Теоретические сведения
Движение электронов по замкнутой орбите эквивалентно круговому току I = e ν, где е - заряд электрона, а ν - частота обращения электрона. При этом модуль орбитального магнитного момента электрона (см. формулы (7)...(9))
Рm орб = е ν π r2 (5.1)
Модуль момента импульса электрона, движущегося по круговой орбите (см. рис.5.1),
Lорб = m r υ = m 2 π ν r2. (5.2)
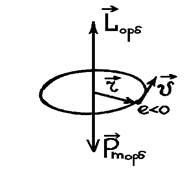 Рис.5.1 Рис.5.1 | Сравнивая формулы (5.1) и (5.2), найдем магнитомеханическое отношение: 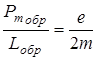 . (5.3) Кроме орбитальных моментов . (5.3) Кроме орбитальных моментов 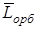 и и 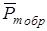 электрон имеет также собственный момент импульса электрон имеет также собственный момент импульса 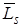 , называемый спином, и собственный магнитный момент Pms, причем , называемый спином, и собственный магнитный момент Pms, причем |
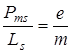 , (5.4)
, (5.4)
что в два раза превышает аналогичное отношение (5.3) для орбитальных моментов. В настоящее время установлено, что именно собственные магнитные моменты электронов ответственны за магнитные свойства многих веществ и, в частности, ферромагнетиков.
Общий магнитный момент атома 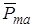 равен сумме орбитальных и собственных магнитных моментов его электронов. Пусть ∆V - небольшой объем пространства, заполненного веществом.
равен сумме орбитальных и собственных магнитных моментов его электронов. Пусть ∆V - небольшой объем пространства, заполненного веществом.
Величину
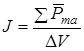 , (5.5)
, (5.5)
где в числителе стоит сумма всех атомных магнитных моментов в объеме DV, называют намагниченностью вещества. Таким образом, 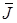 представляет собой магнитный момент единицы объема.
представляет собой магнитный момент единицы объема.
Вектор 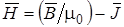 (5.6)
(5.6)
называют напряженностью магнитного поля. Для изотропных магнетиков
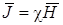 , (5.7)
, (5.7)
где χ - коэффициент, зависящий от рода вещества. Его называют магнитной восприимчивостью.
Вектор 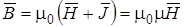 . (5.8)
. (5.8)
Коэффициент μ= 1 + χ называют магнитной проницаемостью вещества. Вещества, для которых χ < 0 (μ<1), называют диамагнетиками. Вещества, для которых χ > 0 (μ>1), называют парамагнетиками. Среди парамагнетиков выделяют класс веществ, называемых ферромагнетиками, для которых: 1) χ (μ) может значительно превышать единицу и 2) χ и μ зависят от H.
Ферромагнетикам свойственно явление гистерезиса. Оно заключается в том, что J зависит не только от H в данный момент, но и от того, как изменилась H в предшествующие моменты времени. Следовательно, для ферромагнетиков J не является однозначной функцией H.
В ферромагнетике имеются микрообласти, в которых все атомные моменты параллельны друг другу даже в отсутствие внешнего магнитного поля. Эти области называют доменами.
Если ферромагнетик поместить в магнитное поле, интенсивность которого постепенно возрастает, то его намагниченность можно довести до насыщения (точка А на рис.5.2) и зависимость 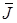 от
от 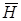 (кривая намагничива-
(кривая намагничива-
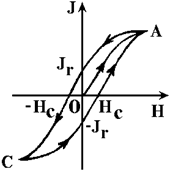 Рис.5.2 Рис.5.2 | ния) выразится участком ОА. При уменьшении 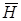 до нуля кривая намагничивания не совпадает с ОА, а идет по АJr, т.е. при снятии внешнего поля до нуля кривая намагничивания не совпадает с ОА, а идет по АJr, т.е. при снятии внешнего поля 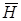 ферромагнетик остается намагниченным с остаточной намагничен-ностью Jr. Для полного размагничивания образца необходимо приложить магнитное поле обратного направления до величины Нc. Величину напряженности Нc называют коэрцитивной силой. При дальнейшем увеличении обратного магнитного поля вновь достигается насыщение J (точка C на рис.5.2). В результате при попеременном изменении направления H зависимость J от Н выразится замкнутой кривой, называемой петлей гистерезиса. Нелинейная зависимость ферромагнетик остается намагниченным с остаточной намагничен-ностью Jr. Для полного размагничивания образца необходимо приложить магнитное поле обратного направления до величины Нc. Величину напряженности Нc называют коэрцитивной силой. При дальнейшем увеличении обратного магнитного поля вновь достигается насыщение J (точка C на рис.5.2). В результате при попеременном изменении направления H зависимость J от Н выразится замкнутой кривой, называемой петлей гистерезиса. Нелинейная зависимость 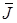 от от 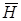 для ферромагнетиков связана с их доменной структурой. Аналогичная предельная петля магнитного гистерезиса для зависимости для ферромагнетиков связана с их доменной структурой. Аналогичная предельная петля магнитного гистерезиса для зависимости 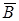 от от 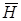 представ- представ- |
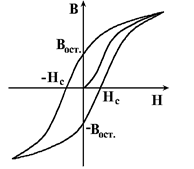 Рис.5.3 Рис.5.3 |
лена на рис.5.3. Величина Вост называется остаточной индукцией. Площадь петли гистерезиса на рис.5.3 пропорциональна количеству теплоты, выделяющемуся в единице объема ферромагнетика за один цикл перемагничивания.
5.2. Описание установки и метода измерений
Схема установки показана на рис.5.4. Исследуемым образцом является ферритовый тороид Т, на который равномерно намотаны две об- мотки 1 и 2 с числом витков N1 и N2 соответственно. Последователь- но с намагничивающей обмоткой 1 включен резистор r1, сопротивление которого равно R1, и миллиамперметр mА. Напряжение с сопротивления R1 подается на горизонтальный вход X осциллографа. Это напряжение пропорционально
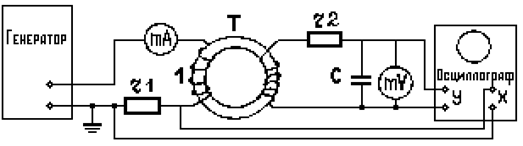 Рис.5.4 Рис.5.4 |
напряженности поля катушки 1, так как через обмотку 1 и резистор r1 течет один и тот же ток. Следовательно, и отклонение луча по горизонтали пропорционально Н.
Для тороида Н = n I, где I - сила тока в тороиде, n - число витков на 1 м тороида (плотность витков).
Миллиамперметр показывает эффективное значение тока Iэф. Амплитуда переменного тока 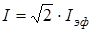 . Таким образом, для амплитуды намагничивающего поля имеем:
. Таким образом, для амплитуды намагничивающего поля имеем:
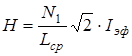 , (5.9)
, (5.9)
где Lср- средняя длина тороида, а 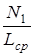 - плотность витков обмотки 1.
- плотность витков обмотки 1.
На вертикальный вход У осциллографа подается напряжение U с конденсатора С. Пренебрегая падением напряжения на вторичной обмотке 2, имеем (по закону Ома): ε = R2J2 - Uс где ε- ЭДС индукции, возникающая в обмотке 2, R2 - сопротивление резистора r2, Uс - напряжение на конденсаторе С. Если R2 и С так велики, что R2J2 » Uc, то
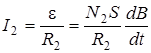 , (5.10)
, (5.10)
где N2 - число витков обмотки 2, а S - площадь сечения тороида.
