Вычисление дирекционных углов и длин линий MA и NB

Параметр	МА, м	NB, м	Исходные данные, м
x1 x2 Dx = x2 - x1	+750,35 +810,40 +60,05	+787,04 +837,43 +50,39	xM = +750.35 yM = +464.28 xN = +787.04 yN= +606.15 aMN = 75°30' aNM = 255°30'   Координаты точек А и В взяты из табл. 16. xA = +810.40 yA = +494.20 xB = +837.43 yB = +569.49
y1 y2 Dy = y2 - y1	+464,28 +494,20 +29,92	+606,15 +569,49 - 36,66
tg r румб r a	+0,49825 CB:26°29'05'' 26°29'05''	- 0,72753 CB:36°02'13'' 323°57'47''
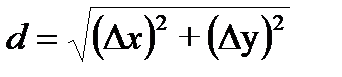	67,09	62,31
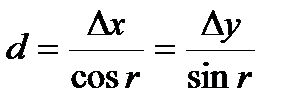	67,09	62,31

Примечание b₁ = a_MN - a_MA = 49°00,9'; b₂ = a_NB - a_NM = 68°27,8'.

По данным разбивочного чертежа (рис. 31) на местности строят углы b₁ и b₂, откладывают расстояния d₁ и d₂ и получают точки А и В, которые закрепляют кольями.

Для контроля измеряют линию АВ, затем построением прямых углов в точках А и В и линий АС и ВD получают точки C и D, которые закрепляются кольями.

Для контроля измеряют ось здания CD и диагонали AD и ВС. Относительная ошибка разности между измеренной и проектной линией должна быть не более 1:2000.

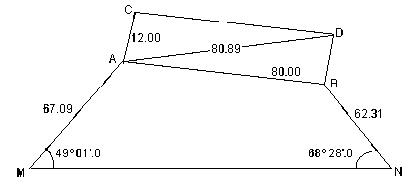
Рис.31.Разбивочный чертеж при разбивке полярным способом

Подготовка разбивочных данных и разбивка здания способом линейных засечек.

Способ линейных засечек применяется на ровной открытой местности, когда проектные расстояния d₁, d₂, d₃, d₄ (рис.32) не превышают длины мерного прибора.

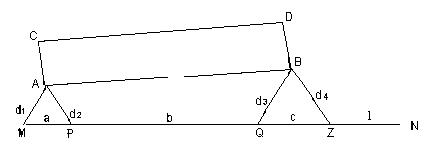
Рис.32. Схема разбивочных элементов при разбивке здания способом линейных засечек

Координаты точек M и N и длина линий d_MN известны (табл.26).

Таблица 26

Исходные данные для разбивки здания способом линейных засечек

Точка	Координаты, м	Длина, м
Х	У
M N	1197,07 1236,61	2402,06 2463,80	72,32

Для решения задачи сначала необходимо определить координаты точек А и В.

Координаты точки А(x_A, y_A) определяются графически по плану с использованием поперечного масштаба и измерителя. Координаты точки В определяют по формулам:

x_B = x_A + d_AB×cosa_АB ;

y_B = y_A + d_AB×sina_A,

где d_AB– проектная длина здания,

a_AB – дирекционный угол линии, определяемый транспортиром по плану.

Результаты вычислений координат точки Вприведены в табл.27.

Таблица 27

Определение координат точки В

Параметр	В
a r d	53°00'00'' CB:53°00'00'' 40,00
x1 Dx x2	+1206,60 +24,07 +1230,67
y1 Dy y 2	+2405,20 +31,94 +2437,14

Затем определяются координаты точек P, Q, Z. Для этого отрезки a, b, c снимают с плана, а отрезок l вычисляют по формуле

l = d_MN - (a + b + c).

Вычисляют значения коэффициентов k_x, k_y (табл.28) по формулам:

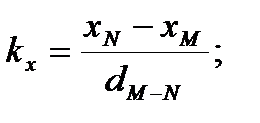
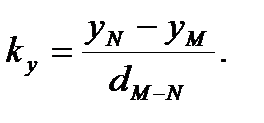
Используя расстояния а, b, c и значения коэффициентов k_x, k_y определяются координаты точек P, Q, Z по формулам:

x_P = x_М + k_x× a; y_P = y_М + k_y× a;

x_Q = x_P + k_x× b; y_Q = y_P + k_y× b;

x_Z = x_Q + k_x× c; y_Z = y_Q + k_y× c.

Для контроля вычисляют координаты точки N

x_N = x_Z + k_x× l; y_N = y_Z + k_y× l.

Таблица 28

Определение коэффициентов k_x,k_y

Параметр	kx,ky
xN xM Dx d	+1236,61 +1197,07 +39,54 73,62
kx	+0,53928
yN yM Dy d	+2463,80 +2402,06 +61,74 73,62
ky	+0,84206

Результаты вычислений координат точек P, Q, Z приводят в табл.29.

Решая обратные геодезические задачи, находят проектные расстояния d₁, d₂, d₃, d₄ (табл.30) и наносят их на разбивочный чертеж (рис.33).

Полевые работы по перенесению на местность точки А способом линейной засечки выполняют в таком порядке:

в точке М закрепляют нулевое деление рулетки с радиусом, равным d₁, прочерчивают на местности дугу, затем нулевое деление рулетки закрепляют в точке Р и прочерчивают дугу радиусом d₂. Точка пересечения дуг является искомой проектной точкой А;

аналогично находят на местности точку В. Для удобства нахождения точек на местности А и В применяют два мерных прибора. Затем построением прямых углов в точках А и В и линий АС и BD получают точки С и D.

Таблица 29