Зависимость между элементами НТС

Между элементами НТС существуют определенные зависимости. Из рисунка следует:

ФПУ = К+ ( ± УС );

УВ = δ − ФПУ;

КУВ = δ − К =УВ + ( ± УС );

УС = ФПУ − К.

Эти зависимости позволяют по двум известным углам определить третий, неизвестный угол. Зависимость между скоростями и углами в навигационном треугольнике скоростей можно установить из того же рисунка по теореме синусов:

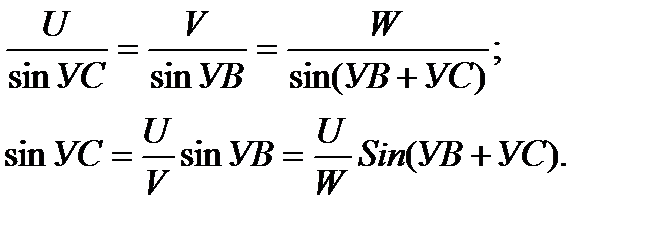
Эти формулы решаются на навигационной линейке НЛ-10М.

Для приближенного определения УС подсчетом в уме может быть получена упрощенная формула. Учитывая, что для современных скоростей полета величина угла сноса обычно не превышает 10 − 15º, а синусы равных углов можно принять равными самим углам, выраженных в радианах, получим:

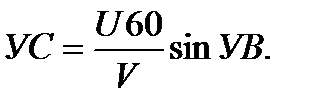
При ветре, перпендикулярном к линии пути, УС максимальный и определяется формулой: 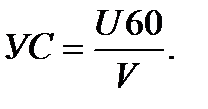или УС = УСмакс · sin УВ.

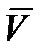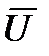Путевую скорость можно определить, проецируя векторы и на направление вектора 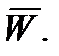В этом случае путевая скорость будет равна:

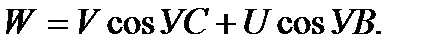
Учитывая небольшую величину углов сноса, можно принять 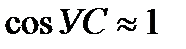и тогда записать приближенное равенство:

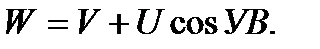
Полученные приближенные формулы углов сноса и путевой скорости используются для решения навигационных задач в уме.

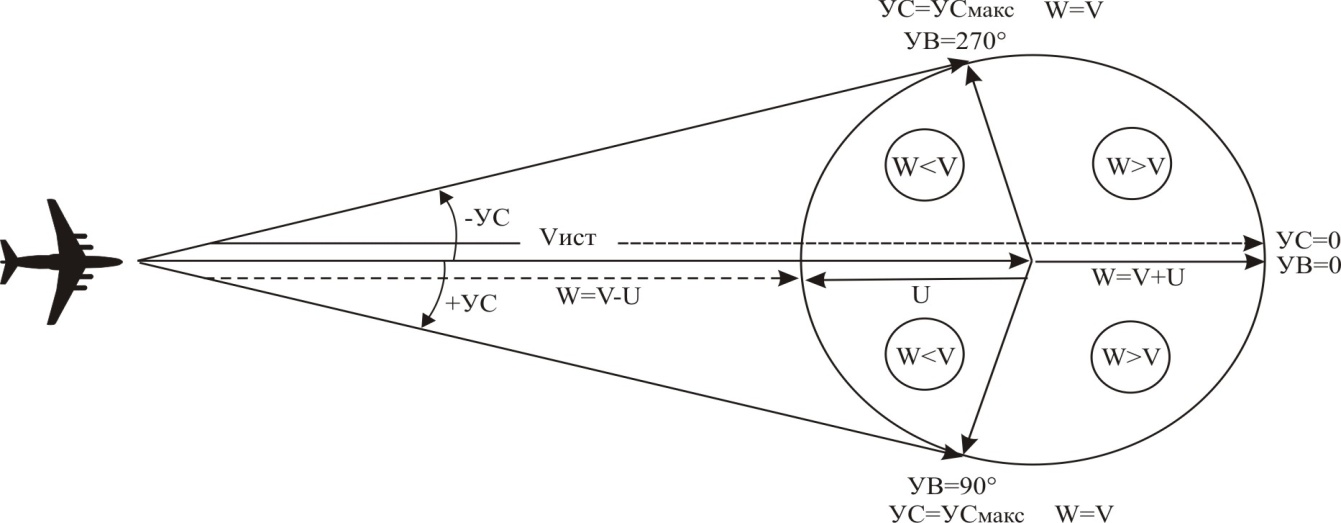
При выполнении полета по маршруту изменяются воздушная скорость (V), направление (δ) и скорость ветра (U), что приводит к изменению угла ветра (УВ), угла сноса (УС) и путевой скорости (W).

УВ=90°; УС=УСмакс; W=V.

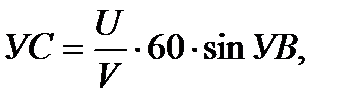Анализируя формулу можно сделать вывод, что угол сноса изменяется пропорционально углу ветра.

0 30 60 90 180 270 360

+УС

УСмакс

УСмакс

–УС

УВ

Для выявления зависимости угла сноса при изменении угла ветра будем вращать вектор ветра по окружности. УВ при этом будет принимать различные значения: от 0° до 360°. Будет изменяться и УС. Изобразим эту зависимость графически:

Из графика и формулы видно, что:

· при УВ, равным 0° и 180° УС будет равен нулю, т.е. векторы воздушной и путевой скорости будут совмещены;

· при УВ 90° и 270° УС достигает максимального значения;

· при УВ от 0° до 180° УС принимает положительный знак, а при УВ от 180° до 360° - отрицательный;

·

Wмакс Wмакс

V

90 180 270 360

Wмин

УВ

при изменении УВ от 0° до 90° и от 180° до 270° УС растет до максимального значения, а при изменении от 90° до 180° и от 270° до 360° уменьшается от максимального значения до нуля;

· одни и те же изменения УВ при попутном или встречном ветре (УВ, близких к 0° или 180°) вызывают значительно большие изменения УС, чем при боковом ветре (УВ, близких к 90° или 270°).

В процессе полета могут изменяться воздушная скорость и скорость ветра. Из формулы 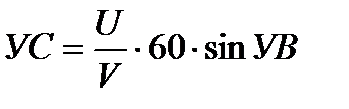видно, что с увеличением V угол сноса уменьшается, а с уменьшением V – увеличивается. При увеличении скорости ветра УС увеличивается, а при уменьшении скорости ветра – уменьшается. В штиль, т.е. когда U равняется нулю, УС отсутствует. В свою очередь, всякое изменение УС при постоянном курсе полета вызывает изменение фактического ПУ, что необходимо учитывать при подготовке и выполнении полета.

Для уяснения характера изменения W при изменении УВ рассмотрим формулу:

W = V ± U · cos УВ.

Из этой формулы видно, что W изменяется пропорционально cosУВ. Рассмотрим зависимость значения составляющей путевой скорости (U·cosУВ) от УВ:

· максимального значения W достигает при УВ, равным нулю (ветер попутный), а минимального – при угле ветра 180°;

· при 90° и 270° (ветер боковой) W примерно равна V;

· при изменении УВ от 0° до 180° W изменяется от максимального до минимального значения;

· одни и те же изменения УВ при боковом ветре (при УВ, близких к 90° и 270°) вызывают значительно большие изменения W, чем при попутном или встречном ветре (при УВ, близких к 0° или 180°);

· при отсутствии ветра W = V;

· при изменении воздушной скорости путевая скорость изменяется примерно на такую же величину, т. е. ∆V ≈ ∆W.

Из анализа изменения УС и W можно сделать вывод, что при попутном и встречном ветре даже небольшое изменение курса вызовет существенное изменение УС(к) и незначительное изменение W, а при боковом – незначительное изменение УС и существенное – путевой скорости (Wк).