Измерение емкости конденсатора и диэлектрической проницаемости

Цель работы: познакомиться с методом измерения емкости конденсатора.

Приборы и принадлежности: генератор низкой частоты, вольтметр (осциллограф), набор сопротивлений и емкостей, набор диэлектрических пластин и модуль МО-З.

Краткая теория

Плоский конденсатор состоит из двух (или более) металлических пластин, между которыми находится диэлектрик с диэлектрической проницаемостью ε. Емкость конденсатора есть отношение заряда q на обкладках конденсатора к той разности потенциалов U,которую этот заряд сообщает конденсатору.

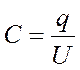(1)

Емкость плоского конденсатора 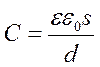(2)

(2)

где ε₀ = 8,85·10^-12 Ф/м, S - площадь поверхности обкладки конденсатора, d - расстояние между обкладками, ε - диэлектрическая проницаемость диэлектрика между обкладками.

Описание установки

Разборный конденсатор смонтирован на модуле МО-3. Нижняя пластина-1 присоединена к клеммам "1" на модуле (рис.1). Верхняя пластина-2 - съемная, она позволяет заменять диэлектрик конденсатора. Для измерения предлагаются три съемных диэлектрических пластины и воздушный зазор.

Толщина пластин диэлектрика и площадь пластин конденсатора указана в табл. 1. Верхняя пластина располагается на упорах 3, обеспечивающих воздушный зазор между пластинами шириной 2 мм. Конденсатор размещен на основании 4, соединенном с общим проводом "4". Подключение к верхней пластине конденсатора производится через клемму 5 в центре пластины.

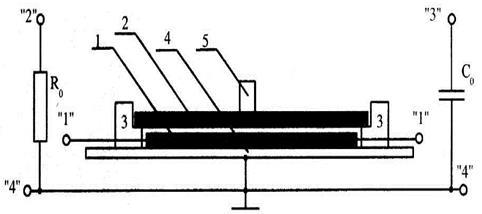
Рис. 1. Разборный конденсатор

Порядок выполнения работы

Задание 1. Измерение электрической емкости конденсатора.

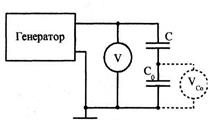
1. Соберите электрическую цепь по схеме на рис. 2. В качестве вольтметра можно использовать электронный осциллограф с входным делителем напряжения. Емкость конденсатора C₀= 10,8 нФ.

2. Включите генератор и осциллограф в сеть. Установите частоту генератора ν =3 кГц, напряжение U = (7 – 10) В.

3.Измерьте напряжение U и U_C0. Результаты измерений занесите в табл. 1.

4.Проделайте измерения со всеми пластинами диэлектрика.

5.Рассчитайте емкость конденсатора при всех данных в работе диэлектриках по формуле (3)

Рис. 2. Электрическая схема

к заданию 1

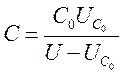(3)

6 . Используя формулу (2), рассчитайте диэлектрическую проницаемость каждого диэлектрика по формуле 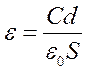(4).

(4)

7. Результаты расчетов занесите в табл.1.

Таблица 1

Диэлектрик	d , мм	S , м2	U, В	UCo, В	С, пФ	ε
Стекло	4,9	2,3 10-2
Оргстекло	4,1	2,3 10-2
Текстолит	4,1
Воздух	2.0

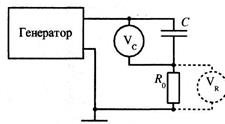1.Соберите электрическую цепь по схеме, изображенной на рис. 3. Проведите измерения аналогичные измерениям в упражнении 1 по пунктам 2-4.

2. Результаты измерений занесите в табл. 2.

3. Рассчитайте емкостьС и
диэлектрическую проницаемость конденсаторов по формулам (3) и (4). Рис.3. Электрическая схема

Заполните табл. 2. (R₀ = 9,8кОм). к заданию 2

Таблица 2

Диэлектрик	d , мм	S , m 2	UR, В	UC, В	С, пФ	ε
Стекло	4,9	23 10-2
Оргстекло	4,1	2,3 ·10-2
Текстолит	4,1
Воздух	2.0

1. Свободные и связанные заряды. Полярные и неполярные диэлектрики. Поверхностная плотность связанных зарядов.

2. Электрическое поле в диэлектрике. Диэлектрическая восприимчивость и диэлектрическая проницаемость. Вектор электрической поляризации и вектор электрического смещения.

3. Теорема Гаусса для электрического поля в диэлектрике.

4. Электроемкость проводников. Конденсаторы. Расчет емкости плоского цилиндрического и др. конденсаторов. Соединения конденсаторов. Емкостное сопротивление.

5. Энергия заряженного проводника и конденсатора. Энергия электрического поля. Объемная плотность энергии.

6. В однородном поле находятся вплотную прижатые друг к другу пластины из слюды и текстолита так, что силовые линии перпендикулярны пластинам. Напряженность поля в текстолите E_Т = 60 В/м. Найти напряженность поля в слюде и вне пластины.

7. Расстояние между обкладками плоского конденсатора увеличивают. Как изменится: а) электроемкость конденсатора, б) напряженность электрического поля, в) напряжение. Рассмотреть два случая: 1) конденсатор заряжен и отключен от источника напряжения; 2) конденсатор подключен к источнику напряжения.

8. Плоский конденсатор состоит из двух пластин, площадью S=200 см² каждая, расположенных на расстоянии d=2 мм друг от друга, между которыми находится слой слюды. Какой наибольший заряд можно сообщить конденсатору, если допустимое напряжение U=3 кВ?

9. К воздушному конденсатору, напряжение на котором U₁=210 В, присоединили параллельно такой же незаряженный конденсатор, но с диэлектриком из стекла. Какова диэлектрическая проницаемость стекла, если напряжение на зажимах батареи стало U=30 В.

10. Пространство между обкладками плоского конденсатора заполнено двумя слоями диэлектрика толщиной d₁ и d₂, которые параллельны обкладкам конденсатора. Диэлектрические проницаемости диэлектриков ε₁ и ε₂ соответственно. Площадь пластин S. Найти емкость конденсатора C.

11. Плоский конденсатор заполнен диэлектриком и на его пластины подана некоторая разность потенциалов. Его энергия при этом равна 2·10^-5 Дж. После того, как конденсатор отключили от источника напряжения, диэлектрик вынули из конденсатора. Работа, которую надо было совершить против сил электрического поля, чтобы вынуть диэлектрик, равна 7·10^-5 Дж. Найти диэлектрическую проницаемость диэлектрика.

ЛАБОРАТОРНАЯ РАБОТА № 4