Связь между дирекционными углами и румбами

Четверть	Дирекционный угол, α	Румб,   r	Знаки приращений координат
номер	название	Δх	Δу
І	СВ	0º – 90º	r=α	+	+
ІІ	ЮВ	90º – 180º	r=180º – α	_	+
ІІІ	ЮЗ	180º – 270º	r=α – 180º	_	_
ІV	СЗ	270º – 360º	r=360º – α	+	_

Рис. 7. Связь между дирекционными углами и румбами

Содержание задания и порядок решения

Исходные данные: заданные на карте точка и отрезок.

Порядок решения:

1. Определяют по карте прямоугольные координаты начальной точки отрезка.

2. Измеряют длину отрезка с помощью поперечного масштаба.

3. Измеряют дирекционный угол отрезка.

4. Вычисляют приращения координат и координаты конечной точки отрезка по формулам (15) и (14).

5. Определяют по карте прямоугольные координаты конечной точки отрезка и сравнивают с вычисленными. Расхождение не должно превышать 3t – утроенной точности масштаба.

Решение задачи выполняют в табл. 8.

Таблица 8

Решение прямой геодезической задачи

Но-ме- ра точек	Длина отрез- ка	Направление линии	Приращения координат, м	Координаты точек, м
α º ′	r º ′	Начальной и конечной	Конечной, определенные по карте
Δх	Δу	X	Y	X	Y
А						v	v
	v	v	v	v	v
В						v	v	v	v

«v» - место записи величин

6.2. Обратная геодезическая задача заключается в нахождении длины (горизонтального проложения) и направления (сначала румба, затем дирекционного угла) отрезка прямой линии по координатам его конечных точек.

Возможны два варианта решения: первый – сначала определяют направление (дирекционный угол), затем длину отрезка; второй – сначала определяют длину отрезка, а затем его направление. Основным считается первый вариант, второй используется для контроля.

Первый вариант решения:

1. Определяют по карте прямоугольные координаты конечных точек отрезка.

2. Вычисляют приращения координат Δх и Δу, вычитая из значений координат конечной точки координаты начальной точки отрезка.

3. Вычисляют румб по формуле

(16)

4. Вычисляют дирекционный угол по формуле зависимости между румбом и дирекционным углом, предварительно определив по знакам приращений координат номер четверти, в которой расположен отрезок (по табл.7)

5. Вычисляют длину отрезка по трем формулам:

(17)

Второй вариант решения:

1.Определяют по карте координаты конечных точек отрезка и вычисляют приращения координат.

2. Определяют длину отрезка по теореме Пифагора

(18)

3.Ввычисляют румб по двум формулам

. (19)

4. Вычисляют дирекционный угол по формулам зависимости между румбом и дирекционным углом (табл.7), если расхождение двух значений румба не превышает точности вычислений.

Результаты вычислений представляют в табл. 9 до целых минут.

Таблица 9

Решение обратной геодезической задачи

Номер точки	Координаты, м	Приращения координат, м	arctg r   Δy/Δx	Румб r	Дир. угол α	Длина отрезка d, м
Х	У	Δх	Δу
A	v	v
			v	v	v	v	v	v	v	v
B	v	v

«v» - место записи величин

Задание №7. Определение крутизны скатов

1. Определить уклон заданной линии, используя ранее вычисленные отметки точек.

2. Определить крутизну ската в конечных точках линии и углы наклона местности.

Мерой крутизны ската служит уклон, обозначаемый буквой i, зависит от угла наклона местности

(20)

т.е. уклон – это тангенс угла наклона, равный отношению превышения h между точками местности к горизонтальному расстоянию d между ними. Уклоны различают положительные (повышения) и отрицательные (понижения).

Уклоны выражают в тысячных долях или в промилле – десятых долях процента. Например, i=0,050, или 50 ‰. Уклон показывает, на сколько метров повышается или понижается линия местности на каждые 1000 м (1 км) расстояния. Например, i=0,025 (25 ‰) означает, что на каждый километр (1000 м) местность повышается на 25 м. Уклоны прямого и обратного направлений равны по величине, но противоположны по знаку.

По карте крутизну ската в любом месте можно определить без вычислений по графику заложений, вычерченному под южной рамкой в правой части карты. График заложений – это кривая линия, расстояния от которой по перпендикуляру до горизонтальной линии равны заложениям. Основание графика оцифровывают в градусах или уклонах.

Для определения крутизны ската берут в раствор циркуля-измерителя кратчайшее расстояние между соседними горизонталями и переносят его на график заложений вертикально так, чтобы одна игла циркуля располагалась на кривой, другая – на горизонтальной линии, и по оцифрованной шкале считывают крутизну ската в данном месте в градусах угла наклона, либо в уклонах, в зависимости от оцифровки.

б)

а)

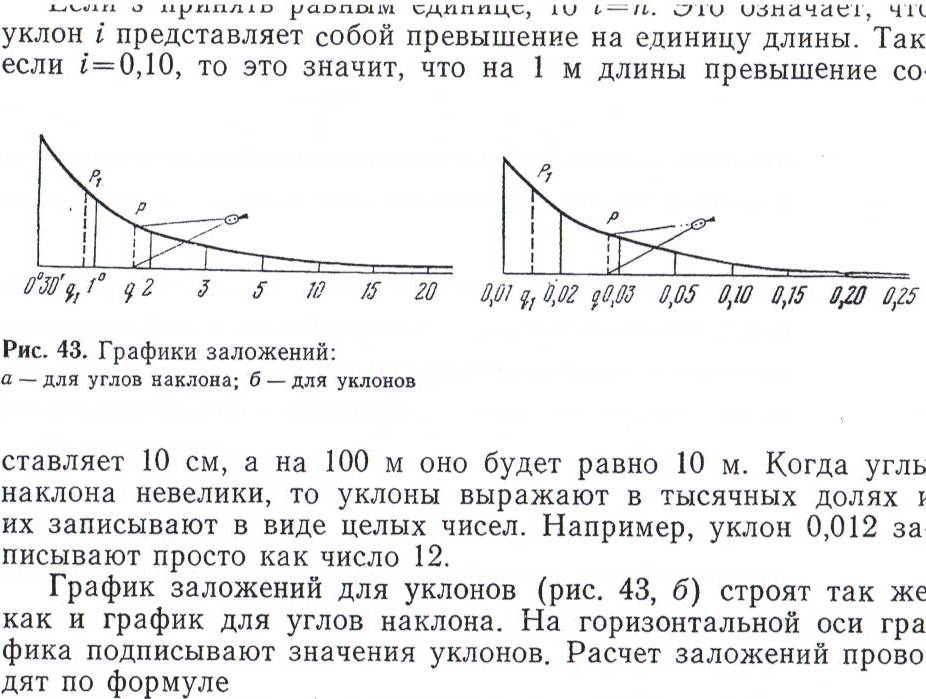
Рис. 8. Графики заложений: а) – для углов наклона, б) – для уклонов

Для углов наклона до 6^о зависимость между ними и уклонами приближенно имеет вид

(21)

где ρ^о=57,3^о – радиан.

Кратчайшее расстояние между горизонталями (заложение) будет соответствовать наибольшей крутизне ската в данной точке.

Задание №8. Построение профиля местности по заданному

Направлению

Построить профиль местности по заданному на карте направлению.

Профилем местности называется уменьшенное изображение на плоскости вертикального разреза земной поверхности по заданному направлению. Разрез местности представляет собой кривую линию, на профиле его изображают в виде ломаной линии с изгибами в точках перегиба рельефа, т.е. в точках изменения крутизны скатов. Отметки точек перегиба рельефа определяют либо измерением на местности, либо по карте. На профиле прямой линией изображают уровенную поверхность, параллельную основной, ей придают условную отметку и называют линией условного горизонта (УГ). Для большей выразительности (наглядности) вертикальные отрезки – высоты – изображают в масштабе в 10 раз крупнее, чем горизонтальные расстояния между точками, т.е. если горизонтальный масштаб 1:5000, то вертикальный 1:500.

По топографической карте профиль строят обычно по горизонталям в следующем порядке. На листе миллиметровой бумаги размером 20х30 см на расстоянии не менее 5 см от нижнего края его выбирают горизонтальную утолщенную линию, которую принимают за основание профиля – линию условного горизонта (УГ). На расстоянии 8-10 см от левого края листа выбирают вертикальную утолщенную линию, на которой размечают шкалу высот через 1 см выше линии условного горизонта. Ниже линии основания профиля и левее линии шкалы высот вычерчивают профильную сетку шириной 60 мм, содержащую две графы: первая (верхняя) – «Отметки», шириной 15 мм; вторая – «Расстояния», шириной 10 мм.

Профиль местности по линии АВ

Масштабы: горизонтальный 1:2000 Вертикальный 1:200

Выполнил студент Гр. П – 201 Иванов В. А.

Рис. 9. Пример построения профиля местности по горизонталям

Затем вдоль заданной на карте линии отмечают и определяют интерполированием отметки пересекаемых ею горизонталей, характерных линий рельефа (водоразделов и тальвегов), перегибов скатов. Определяют расстояния между соседними отмеченными точками и откладывают их в графе «Расстояния» в заданном горизонтальном масштабе, отделяя вертикальной перегородкой. Числовое значение расстояния записывают горизонтально посередине графы.

В графу «Отметки» на продолжении перегородок графы «Расстояния» записывают вертикально отметки горизонталей и всех остальных отмеченных на линии точек, определенных интерполированием между горизонталями.

Выбирают отметку линии условного горизонта, кратную 10 м или 5 м такую, чтобы отстояния от нее до точки с наименьшей отметкой было не менее 3 см в заданном вертикальном масштабе. Эту отметку подписывают над профильной сеткой (рис. 9), стрелкой указывают линию, к которой относится отметка.

Шкалу высот подписывают отметками через 1 см относительно условного горизонта в заданном вертикальном масштабе. В отмеченных в графе «Расстояния» точках восстанавливают перпендикуляры к линии основания профиля и, пользуясь шкалой высот, откладывают на них отметки точек.

Соединяют конечные точки соседних перпендикуляров прямыми линиями и получают ломаную линию профиля, которую вычерчивают черной тушью. Толщина линии 0,3 мм.

Над профилем подписывают заголовок: «Профиль местности по линии АВ». Ниже профиля подписывают масштабы и кто выполнил: М_Г 1:5000, М_В 1:500; Выполнил студ. Гр. Ад-166 (Фамилия и инициалы).

Профиль может быть построен также по точкам через равные интервалы, обычно равные 100м, называемые пикетами и дополнительным (плюсовым) точкам на пересечении заданной линии с водораздельными и водосливными линиями и изменения крутизны скатов. В этом случае заданную линию разбивают на равные отрезки и отмечают дополнительные точки. В графе «Расстояния» откладывают отрезки равные заданному интервалу, а также расстояния между пикетами и плюсовыми точками (характерными точками рельефа и перегибами его). Определяют отметки намеченных точек интерполированием между горизонталями и записывают в графу «Отметки». Затем строят линию профиля, как указано выше.

Задание №9. Построение линии с заданным уклоном

Построить линию с уклоном, заданным преподавателем, между двумя точками.

При проектировании инженерных сооружений линейного типа на равнинных участках трассу – ось линейного сооружения – проектируют по прямой линии между точками. Во всхолмленной и горной местности трассу проектируют как кратчайшую линию между заданными начальной и конечной точками так, чтобы на всем протяжении ее уклон ни в одной точке не превышал заданной или допустимой величины.

Для проведения такой линии на карте по заданному (или допустимому) уклону вычисляют соответствующее ему расстояние между горизонталями по формуле: (22)

Это расстояние в масштабе карты берут в раствор циркуля, ставят ножку (иглу) на начальную точку и засекают первую горизонталь в направлении воздушной линии между начальной и конечной заданными точками и отмечают точку. Из полученной точки засекают этим раствором циркуля следующую горизонталь и последовательно все остальные горизонтали. Соединяют отмеченные на соседних горизонталях точки и получают ломанную линию, уклон которой на всех отрезках не превышает заданного (рис.10). Если вычисленное расстояние меньше расстояния между горизонталями, то трасса идет по прямому направлению к конечной точке.

Расстояние d может быть взято в раствор циркуля с графика заложений.

Как правило, строят два варианта трассы в обход препятствия.

Рис. 10. Проектирование линии заданного уклона

Задание №10. Определение площади участка

Определить площадь участка, отмеченного на карте.

Так как на картах расстояния между точками являются уменьшенными горизонтальными проложениями наклонных линий местности, то при определении площадей необходимо учитывать углы наклона местности. Существует несколько способов определения площадей по картам: графический, графо-аналитический, механический, аналитический и их разновидности.

Графический способ определения площадей по картам предусматривает использование различного рода палеток на прозрачной основе, имеющих вид сетки квадратов со стороной 2-4 мм, каждый из которых является единицей измерения площади. Палетку накладывают на криволинейный контур и подсчитывают сначала число целых квадратов внутри участка, затем, оценивая на глаз доли неполных квадратов, суммируют их. Площадь участка равна произведению площади одного квадрата на число всех квадратов.

Если контур участка имеет вид ломаной линии, то его разделяют на элементарные геометрические фигуры (треугольники, прямоугольники, квадраты), вычисляют площади каждой из них по формулам геометрии и суммированием их получают общую площадь участка

(23)

Графо-аналитический способ заключается в измерении по карте расстояний (горизонтальных проложений) и определении высот угловых точек участка интерполированием по горизонталям. По этим данным вычисляют наклонные расстояния

(24)

где - горизонтальное проложение на местности;

h – превышение между конечными точками линии;

d – длина отрезка на карте.

Отметки угловых точек контура определяют интерполированием по горизонталям.

Затем вычисляют площади по формулам, соответствующим форме контура:

треугольника , где а – основание, b – высота треугольника;

квадрата , где а – сторона квадрата;

трапеции , где а и с – основания, b – высота трапеции;

прямоугольника , где а и b – стороны прямоугольника.

Если контур участка криволинейный, то его площадь определяют механическим способом, используя специальный прибор планиметр.

В аналитическом способе площадь контура вычисляют по координатам точек поворота, определенным по результатам измерений на местности или по карте по формулам:

(25)

где n – число вершин многоугольника;

i – порядковый номер точки поворота контура.

Задание №11. Определение водосборной площади

Определить водосборную площадь, заданную преподавателем.

Водосборной площадью (водосборным бассейном или просто водосбором) называется территория, ограниченная водораздельными линиями и створом линейного сооружения поперек долины. Она используется для определения количества атмосферных осадков, выпадающих на данной территории, при проектировании гидротехнических сооружений (плотин, дамб и др.) и водопропускных сооружений (труб, мостов и др.) на автомобильных и железных дорогах. Для ее определения на карте проводят линию поперек долины (ось будущего сооружения) иводораздельную линию по осям двух соседних хребтов (по нормалям к горизонталям), через две вершины и перевал. Площади между водоразделами, тальвегом и сооружением определяют с учетом крутизны скатов (склонов). По количеству атмосферных осадков, выпадающих на данной территории на единицу площади (по данным ближайшей метеостанции), рассчитывают объем стока воды, а по нему – размеры гидротехнических и водопропускных сооружений.

Задание №12. Определение объемов земляных масс

Определить объем земляных масс формы рельефа, заданной преподавателем.

По карте можно вычислить объемы земляных масс выпуклых (гора, холм, сопка) и вогнутых (котловина) форм рельефа.

Для приближенного вычисления объема форму рельефа считают усеченным конусом. Определяют площади нижнего S_Н и верхнего S_В оснований, ограниченные горизонталями у подошвы и вершины горы или у бровки и дна котловины и высоту h конуса как разность отметок верхней и нижней горизонталей и вычисляют объем V усеченного конуса

, (26)

где S_H и S_B – площади нижнего и верхнего оснований конуса;

h – высота конуса.

Затем вычисляют объем, заключенный между верхней горизонталью и вершиной и нижней горизонталью котловины и ее дном по формулам

(27)

где h_B – высота от верхнего основания конуса до вершины;

h_H – высота от нижнего основания конуса котловины до дна.

Общий объем равен

(28)

Если отметка вершины горы или дна котловины на карте не подписана, то ее принимают на половину высоты сечения рельефа больше на вершинах и меньше в котловинах отметки последней горизонтали.

Для более точного определения объема вычисляют объемы усеченных конусов между двумя соседними горизонталями, принимая h = h_сеч., а затем общий объем как сумму объемов всех усеченных конусов:

, (29)

где к – число частных объемов.

Задание №13. Ориентирование карт на местности

Изучить способы ориентирования карт на местности.

При пользовании картой на местности возникает необходимость ориентирования ее относительно сторон света.

Ориентировать карту на местности – значит расположить ее в горизонтальной плоскости так, чтобы линии карты стали параллельны соответствующим линиям местности. Ориентировать карту можно:

- по местным предметам;

- по магнитному меридиану с помощью буссоли или компаса;

- по истинному меридиану, если направление его известно.

Для ориентирования карты по местным предметам прежде всего опознают (идентифицируют) на карте точку стояния. Затем выбирают на местности другую точку, имеющуюся на карте, поворачивают лист так, чтобы направление на нее на карте совпало с направлением на местности. При этом удобно пользоваться визирной линейкой (трехгранной). Прикладывают край линейки к точкам стояния и ориентирования на карте, поворачивают лист карты до тех пор, пока выбранная точка не будет находиться на продолжении верхнего ребра линейки (на визирной линии).

При ориентировании карты по магнитному меридиану необходимо учитывать склонение магнитной стрелки. Отсчет по северному концу магнитной стрелки устанавливают равным величине склонения ее.

При правильно ориентированной карте направления на все точки местности будут соответствовать направлениям на карте.

Задание №14. Разграфка и номенклатура топографических карт и планов

Изучить системы разграфки и номенклатуры топографических карт и планов масштабного ряда. Определить номер шестиградусной зоны по трем признакам.

Хотя земную поверхность изображают на картах и планах в уменьшенном виде, ее невозможно представить на одном листе в любом масштабе. Поэтому карту разделяют на отдельные листы, формат которых удобен для практического пользования и издания, обычно от 60х60см до 80х80см, но изображаемая на них территория не одинаковая, зависит от масштаба. Разделение многолистной карты на отдельные листы по определенной системе называется разграфкой. Так как границами изображенной на карте территории являются отрезки дуг параллелей и меридианов, то разграфкой по сути являются размеры листа карты в градусной мере по широте и долготе:

. (30)

Разграфкой топографических карт служат географические координаты углов рамки листа карты (точек пересечения меридианов и параллелей).

Для однозначного определения местоположения каждого листа карты на земной поверхности введено понятие номенклатуры.

Номенклатурой называется обозначение (нумерация) отдельных листов карты по определенной системе. Номенклатура подписывается над северной стороной внешней рамкой посередине листа карты.

В нашей стране в основу разделения на листы и их обозначение положена международная разграфка и номенклатура листа карты масштаба 1:1000000, получаемая делением земной поверхности параллелями через 4⁰ на широтные ряды (или пояса), обозначаемые заглавными буквами латинского алфавита от А до V, к северу и югу от экватора и меридианами через 6⁰ на колонны, нумеруемые арабскими цифрами от 1 до 60, начиная от меридиана 180⁰ в направлении с запада на восток. В результате такого деления получаются трапеции, стороны которых являются внутренними рамками листов карт масштаба 1: 1000000. Номенклатура листа карты масштаба 1:1000000 состоит из буквы широтного ряда и номера колонны, например L-43.

Средние меридианы трапеций совмещают с осевыми меридианами шестиградусных зон Гаусса – Крюгера, счет которых ведется от Гринвичского меридиана. Поэтому номер зоны n меньше номера колонны N на 30 единиц: N – n =30. Первая зона совпадает с 31 колонной. Долготы осевых меридианов карт миллионного масштаба вычисляют по формуле: λ₀=6⁰·n–3⁰. Номер зоны получают делением долготы на 6 градусов, округляя дробное число до целого в большую сторону. Например, точка с долготой 18⁰ 07’ 30” находится в 4 зоне: 18⁰ 07’30” : 6 = >3= 4. Номер зоны приписывают к ординатам координатных линий слева.

Лист карты масштаба 1:1000000 делят последовательно на целое число карт более крупного масштаба, номенклатура которых включает номенклатуру листа карты масштаба 1:1000000, а для карт масштаба 1:50000 и крупнее также и номенклатуру листа карты масштаба 1:100000. Номенклатура планов масштаба 1:5000 не связана с номенклатурой предыдущего масштаба, она получается делением листа 1:100000 на 256 частей. В табл. 10 приведена система разграфки и номенклатуры в нашей стране. Примеры разграфки и номенклатуры карт приведены на схеме ниже.

Если номенклатура на листе карты утрачена, то ее можно восстановить по подписанным на сторонах рамки номенклатурам соседних листов. Номер шестиградусной зоны можно определить по трем признакам на карте: 1) по номенклатуре, вычтя из номера колонны 30; 2) по ординатам подписанным у координатных линий (три последние цифры являются ординатой, а одна или две первые – номер зоны); 3) по долготе, делением ее на 6 градусов, как указано выше.

Таблица 10

Разграфка и номенклатура топографических карт и планов

Масштаб карты, плана	Разграфка	Номенклатура	Обозначение листов
Исходный масштаб	Число листов	Размер листа
по широте Δφ	по долготе Δλ
1:1000000	1:1000000		40	60	М-37	А,B,…,V 1,2,3…59,60
1:500000	1:1000000		20	30	М-37-А	А, Б, В, Г
1:300000	1:1000000		1020’	20	I-M-37	I,II,III…VIII,IX
1:200000	1:1000000		40’	10	M-37-I	I,II,III…XXXV,XXXVI
1:100000	1:1000000		20’	30’	M-37-1	1,2,3,…,143,144
1:50000	1:100000		10’	15’	M-37-144-A	А,Б,В,Г
1:25000	1:50000		5’	7’30’’	M-37-144-A-a	а,б,в,г
1:10000	1:25000		2’30’’	3’45’’	M-37-144-A-a-1	1,2,3,4
1:5000 *)	1:100000		1’15’’	1’52,5’’	M-37-144-(256)	1,2,3…255,256
1:2000*)	1:5000		25’’	37,5’’	M-37-144-(256-a)	а,б,в,г,д,е,ж,з,и

*)на участках площадью больше 20км².

Листы карт масштабов 1:200000 и 1:300000 обозначают римскими цифрами, а остальных масштабов – арабскими цифрами.

Для топографических планов, создаваемых в местной системе координат на площади до 20км², применяется квадратная разграфка, в которой за основу берется масштаб 1:5000, обозначаемый арабскими цифрами, с номера 1.

Таблица 11

Разграфка и номенклатура планов в местной системе координат

Масштаб плана	Разграфка	Номенклатура	Обозначение листов
Исходный масштаб	Число листов	Размер листа
по широте	по долготе
1:5000	1:5000		40 см	40 см	1,2,3….n
1:2000	1:5000		50 см	50 см	1-A	А, Б, В, Г
1:1000	1:2000		50 см	50 см	1-A-I	I,II,III,IV
1:500	1:2000		50 см	50 см	1-A-16	1,2,3…14,15,16

Схема расположения планов

1:5000 1:2000 1:1000 1:500

IV

III

III

IV

А

Б

В

Г

А

Б

В

Г

I

II

I

III

II

I

I

IV

III

IV

II

I

Б

А

Г

В

0

1–А, Б, В, Г 1–А–I, II, III, IV 1–A–1,2…15,16

Примечание. Номер листа следующего масштаба приписывают к номенклатуре исходного масштаба.

Вопросы для самопроверки

1. Что называется масштабом?

2. Что обозначает числовой масштаб?

3. Какие задачи решают с помощью масштаба?

4. Что называется точностью масштаба?

5. Объекты местности каких размеров не изображают на картах?

6. Как выбрать масштаб создаваемой карты?

7. Какие две задачи решают с помощью точности масштаба?

8. Где начало географической системы координат?

9. Где начало плоских прямоугольных координат в зональной

системе координат?

10. Что такое преобразованная ордината?

11. Что такое широта и долгота точки?

12. Что значит отметка точки?

13. Что такое горизонталь?

14. Что называется истинным азимутом, магнитным

азимутом, дирекционным углом и румбом?

15. Что такое приращение координат?

16. Что такое разграфка и номенклатура карты?

17. Что такое угол наклона и уклон линии ?

18. Сформулируйте прямую и обратную геодезические задачи.

19. Что называется профилем местности?

20. Что называется горизонтальным проложением?

21. Что такое водосборная площадь?

22. Как определяют объем земляных масс по карте?

23. Как ориентируют карту на местности?

24. Как строят линию заданного уклона?

25. Как по карте определяют отметки точек местности?

26. Какими способами определяют площади участков по карте?