Математические модели распространения примеси

Гауссова модель

Загрязняющий воздух промышленный выброс воздушными потоками выносится из района расположения источника на значительное расстояние. Скорость и дальность переноса загрязнения зависит от турбулентности воздуха и существующего во время эмиссии загрязнения ветрового поля. Перенос выброса в атмосферном воздухе, как правило, относится к гауссову типу переноса, поскольку среднее сечение выброса (факела) очень сходно с видом распределения Гаусса, имеющего форму колокола.

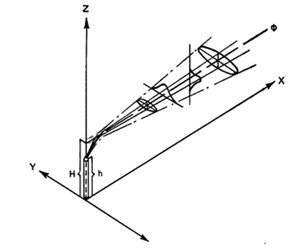
Рис.1 – Идеализированный выброс гауссова типа

Здесь Ф - сечение выброса перпендикулярно направлению движения, h - высота трубы, H - общая высота выброса, которая является суммой высоты трубы и добавочной высоты, на которую поднимается выброс.

Для расчета средних значений концентрации примеси в экологически значимой зоне часто используют гауссову модель распространения примеси.

Согласно этой модели, изменения концентрации примеси от мгновенного точечного источника примеси подчиняется нормальному закону распределения:

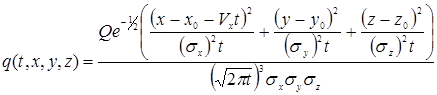(1)

Где 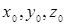- координаты источника примеси;

Q - мощность источника;

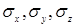- средние квадратичные отклонения частиц примеси в момент времени t соответственно вдоль координатных осей OX, OY, OZ:

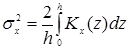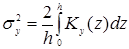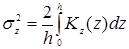, , (2)

V_x - коэффициент, характеризующий скорость ветра;

h - высота приземного слоя.

Используя принцип суперпозиции, из (1) легко получить формулы для расчета концентрации примеси от точечного источника непрерывного действия, мгновенного линейного источника, линейного источника непрерывного действия, мгновенного площадного источника, площадного источника непрерывного действия, мгновенного объемного источника, объемного источника непрерывного действия, если источник является точечным непрерывного действия, то:

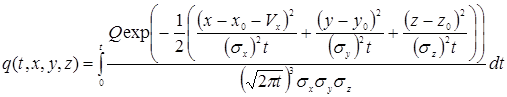, (3)

где

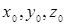- координаты источника примеси;

Q - мощность источника примеси;

V_x - коэффициент, характеризующий скорость ветра в предположении, что система координат сориентирована таким образом, что OX совпадает с направлением ветра.

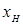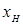Если источник представляет собой более сложное чем точка тело, то и и 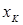- абсциссы начала и конца источника соответственно;

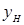и 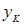- ординаты начала и конца источника соответственно;

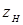и 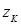- аппликаты начала и конца источника соответственно.

При рассмотрении источников примеси непрерывного действия вводится параметр 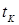- время действия источника (предполагается, что источник примеси начал свою работу в момент времени (t = 0).

Расстояние, на котором регистрируется максимальная концентрация загрязнения в приземном воздухе, зависит и от условий турбулентного обмена в атмосфере. Анализируя отдельные выражения, входящие в уравнение, т.е. 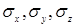можно оценить воздействие турбулентности воздуха на размывание (рассеяние) выброса загрязнения. Скорость ветра в значительной мере влияет на значения этих стандартных отклонений. Такой вывод следует из того факта, что скорость ветра связана со структурой турбулентности в атмосферном воздухе и определяет количество воздуха, которое разбавляет загрязняющие вещества в выбросе при действии процессов турбулентного обмена.

Главным преимуществом гауссовой модели является ее относительная простота. Несмотря на простоту данной модели, наблюдается хорошее согласование экспериментальных и расчетных данных, полученных с помощью данной модели.

Заметим, что гауссова модель рассеяния примеси была получена эмпирическим путем и теоретически обоснована только для наземных источников. Однако позднее она была перенесена без должного обоснования и для случая высотных источников, где ее применение давало результаты, значительно отличающиеся от экспериментальных. Поэтому встал вопрос о создании эффективных аналитических решений более точных моделей рассеяния примеси хотя бы для некоторых наиболее часто встречающихся на практике случаев. В следующем параграфе будет рассмотрено одно из численных решений гауссовой модели рассеяния примеси в атмосфере для линейного непрерывного действия. [5]

ANSYS/FLOTRAN

Модуль Flotran конечноэлементного комплекса ANSYS позволяет решать различные гидро- и аэродинамические задачи, включая задачи о распространении примесей, в том числе и задачи об исследовании процессов распространения выбросов в приземном слое атмосферы. Имеется возможность учитывать тепломассоперенос и турбулентность. В этом случае модуль ANSYS/Flotran использует уравнения непрерывности для каждой примеси, уравнение Навье-Стокса и уравнение энергии.

Модуль позволяет рассматривать задачи: с одним источником выброса и одной примесью, с одним источником выброса и двумя примесями, с двумя источниками выброса, решенными при разных граничных условиях и получать графики распределения концентраций примесей в различные моменты времени после выброса. [6]

ПРАКТИЧЕСКАЯ ЧАСТЬ