Порядок выполнения работы. 1. Вращая маятник за спицы A, намотать нить на шкив B и поднять груз C массой m
1. Вращая маятник за спицы A, намотать нить на шкив B и поднять груз C массой m, указанной на нем, на максимально возможную высоту h и измерить ее линейкой
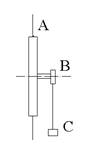 2. Измерить время падения груза. Придерживая одной рукой маятник за любой из стержней, другой коснуться головки секундомера. Одновременно нажать головку секундомера и отпустить стержень маятника. В момент удара груза о подставку снова нажать на головку секундомера, остановив его. По секундомеру отсчитать t падения груза. Опыт повторить 5 раз, беря одно и то же h. Определить среднее время < t > падения груза. Подсчитать вращающий момент Mz по формуле
2. Измерить время падения груза. Придерживая одной рукой маятник за любой из стержней, другой коснуться головки секундомера. Одновременно нажать головку секундомера и отпустить стержень маятника. В момент удара груза о подставку снова нажать на головку секундомера, остановив его. По секундомеру отсчитать t падения груза. Опыт повторить 5 раз, беря одно и то же h. Определить среднее время < t > падения груза. Подсчитать вращающий момент Mz по формуле
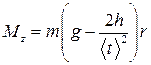
и угловое ускорение ε по формуле
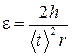 ,
,
r = 2 см – радиус шкива B, на который намотан шнур.
3. То же самое проделать, добавляя к грузу перегрузки (масса каждого перегрузка указана на нем).
4. Данные измерений и вычислений занести в таблицу.
| m, г | t, с | < t >, с | ε, с-2 | Mz, Н·м |
| 11,3 | 10,94 | 0,41 | 0,01 | |
| 10,9 | ||||
| 11,1 | ||||
| 10,65 | ||||
| 9,4 | ||||
| 8,35 | 8,46 | 0,68 | 0,29 | |
| 8,4 | ||||
| 8,6 | ||||
| 8,5 | ||||
| 8,3 | ||||
| 6,9 | 6,89 | 1,03 | 2,082 | |
| 6,76 | ||||
| 6,82 | ||||
| 6,92 | ||||
| 6,98 |
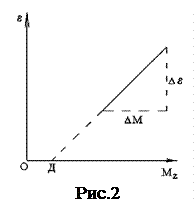
5. Построить график зависимости ε(Mz).
6. Определить по графику (см. рис.2):
а) момент инерции крестовины 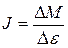 = 2,375
= 2,375
б) момент силы трения Mтр= 0,01 ,
модуль которого равен отрезку ОД.
Контрольные вопросы
1. Описать маятник Обербека.
2. Записать законы и уравнения движения для груза и маятника Обербека.
 3. Как практически на маятнике Обербека можно изменить момент инерции и момент сил? От чего зависит время движения груза?
3. Как практически на маятнике Обербека можно изменить момент инерции и момент сил? От чего зависит время движения груза?
4. Дать определение угловому ускорению и моменту сил. Как определить модуль и направление углового ускорения, момента силы, вращающего маятник?
5. На рисунке представлены два графика зависимости углового ускорения от момента инерции при постоянных моментах М внешних сил. Какой из этих моментов больше?
 6.На барабан радиусом R = 0,5 м намотан шнур, к концу которого привязан груз массой m = 10 кг. Груз опускается с ускорением a = 2 м/с2. Момент инерции барабана равен ...
6.На барабан радиусом R = 0,5 м намотан шнур, к концу которого привязан груз массой m = 10 кг. Груз опускается с ускорением a = 2 м/с2. Момент инерции барабана равен ...
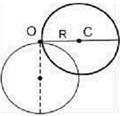
7.Тонкий обруч радиусом 1 м, способный свободно вращаться вокруг горизонтальной оси, проходящей через точку О перпендикулярно плоскости рисунка, отклонили от вертикали на угол 90° и отпустили. В начальный момент времени угловое ускорение обруча равно ...
а) 20 с–2 б) 7 с–2 в) 5 с–2 г) 10 с–2
8.При выстреле орудия снаряд вылетел из ствола с угловой скоростью w = 200 с–1 под углом a =60° к горизонту. Момент инерции снаряда относительно его продольной оси I = 15 кг×м2, растояние между колесами орудия 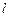 = 1,5 м, время движения снаряда в стволе
= 1,5 м, время движения снаряда в стволе 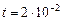 с. Силы давления (в килоньютонах) земли, действующие на колеса во время выстрела, отличаются на ...
с. Силы давления (в килоньютонах) земли, действующие на колеса во время выстрела, отличаются на ...
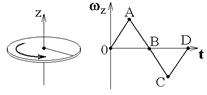 9. Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости так, как показано на рисунке. На каких участках графика зависимости
9. Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости так, как показано на рисунке. На каких участках графика зависимости 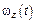 вектор угловой скорости
вектор угловой скорости 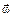 и вектор углового ускорения
и вектор углового ускорения 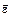 направлены в одну сторону?
направлены в одну сторону?
1) 0 - А и А-В 2) 0 -А и В - С 3) В - С и С - D
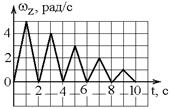 4) всегда направлены в одну сторону
4) всегда направлены в одну сторону
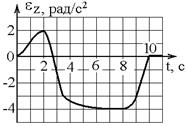
10. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. В какой момент времени угол поворота тела относительно начального положения будет максимальным?
а) 10 с б) 1 с в) 2 с г) 9 с
 11. Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции углового ускорения от времени показана на графике. Во сколько раз отличаются величины тангенциальных ускорений точки на краю диска в моменты времени t1 = 2 с и t2 =7 с?
11. Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции углового ускорения от времени показана на графике. Во сколько раз отличаются величины тангенциальных ускорений точки на краю диска в моменты времени t1 = 2 с и t2 =7 с?
а) в 2 раза б) в 4 раза в) оба равны нулю г) трудно определить точно
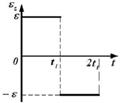 12.Твердое тело начинает вращаться вокруг оси Z. Зависимость углового ускорения
12.Твердое тело начинает вращаться вокруг оси Z. Зависимость углового ускорения 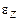 от времени представлена на графике. Соответствующая зависимость угловой скорости
от времени представлена на графике. Соответствующая зависимость угловой скорости 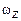 от времени представлена графиком ...
от времени представлена графиком ...
а) 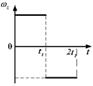 б)
б) 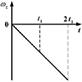 в)
в) 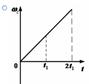 г)
г) 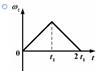
Литература
Савельев И.В. Курс общей физики. т.1. М:Наука, 1986.- гл.III, §29, гл.V, § 38, 39,
