Колебательные спектры поглощения двухатомных молекул
Поглощение в области 102 – 103 см-1 обусловлено обычно колебательными переходами при неизменном электронном состоянии молекулы; соответствующие спектры называют колебательными. Точнее их следовало бы называть колебательно-вращательными, так как изменение колебательной энергии молекулы при поглощении в этой области сопровождается, как правило, изменением и вращательной энергии:
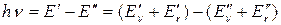 (38)
(38)
На рис. 10 приведен колебательный спектр поглощения газообразного оксида углерода. Он состоит из ряда довольно далеко отстоящих друг от друга полос, интенсивность которых с ростом волнового числа резко убывает. Первую, наиболее интенсивную полосу называют основной полосой, или основным тоном. Далее располагаются 1-й и 2-й обертоны. Интенсивность последующих полос убывает настолько резко, что уже 3-й и 4-й обертоны для большинства молекул наблюдать не удается.
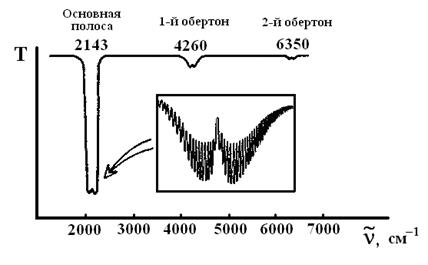
Рис. 10. Колебательный спектр поглощения СО (схема)
Характер изображенного на рис.10 спектра является типичным для гетероядерных двухатомных молекул.
Каждая полоса в спектре является сложной и при записи на приборе с большой разрешающей способностью[3] распадается на ряд отдельных линий (см. врезку на рис.10). Появление такой тонкой структуры характерно для веществ в газообразном состоянии. Положение полос в спектре определяется колебательными переходами, а тонкая структура каждой полосы – вращательными переходами.
Для того чтобы понять происхождение такого спектра, рассмотрим вначале только колебательное движение и колебательные переходы, абстрагируясь от вращения молекулы, т.е. примем, что 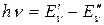 .
.
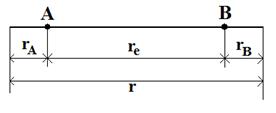
Рис. 11. Схема колебательного движения двухатомной молекулы
Колебательное движение двухатомной молекулы с точки зрения классической механики можно представить как периодическое изменение расстояния между ядрами (рис.11). Если равновесное межъядерное расстояние равно re, а общее изменение длины связи при колебании rA + rB, то согласно закону Гука, описывающему гармонические колебания, сила, возвращающая ядра в положение равновесия, пропорциональна, смещению ядер из положения равновесия:
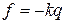 (39)
(39)
где 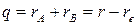 – колебательная координата, k - силовая постоянная.
– колебательная координата, k - силовая постоянная.
Силовая постоянная является важной характеристикой молекулы. Ее физический смысл вытекает из условия: q=1, то 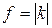 . Силовая постоянная двухатомной молекулы есть величина, характеризующая упругость связи и численно равная силе, деформирующей (растягивающей или сжимающей) связь на единицу длины.
. Силовая постоянная двухатомной молекулы есть величина, характеризующая упругость связи и численно равная силе, деформирующей (растягивающей или сжимающей) связь на единицу длины.
Исходя из модели гармонического осциллятора потенциальная энергия двухатомной молекулы описывается уравнением:
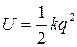 (40)
(40)
При подстановке этого выражения в уравнение Шредингера
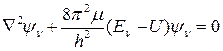 (41)
(41)
и решении этого уравнения получается следующее уравнение для собственных значений колебательной энергии двухатомной молекулы:
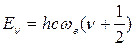 (42)
(42)
где 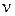 – колебательное квантовое число, принимающее значения целых положительных чисел, начиная с нуля (
– колебательное квантовое число, принимающее значения целых положительных чисел, начиная с нуля ( 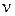 =0, 1, 2, 3 и т.д.);
=0, 1, 2, 3 и т.д.); 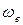 – колебательная постоянная, или собственная частота, характеризующая частоту колебаний, отнесённую к минимуму потенциальной кривой, т.е. ту частоту, которую согласно классической механике имела бы молекула для бесконечно малой амплитуды колебаний (q=0, r=re).
– колебательная постоянная, или собственная частота, характеризующая частоту колебаний, отнесённую к минимуму потенциальной кривой, т.е. ту частоту, которую согласно классической механике имела бы молекула для бесконечно малой амплитуды колебаний (q=0, r=re).
Колебательная постоянная ωe для гармонического осциллятора связана с силовой постоянной следующим соотношением:
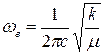 (43)
(43)
где μ-приведённая масса молекулы.
Силовые постоянные двухатомных молекул имеют порядок 102-103 Н/м, или ~0.1-10 мдин/Å.
Энергия колебаний гармонического осциллятора возрастает прямо пропорционально квантовому числу ν, что соответствует системе равноотстоящих квантовых уровней (рис. 12). Согласно квантовомеханическим правилам отбора для гармонического осциллятора возможны переходы с 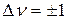 . При поглощении света гармоническим осциллятором колебательное квантовое число изменяется на +1, увеличивается энергия и амплитуда колебаний.
. При поглощении света гармоническим осциллятором колебательное квантовое число изменяется на +1, увеличивается энергия и амплитуда колебаний.
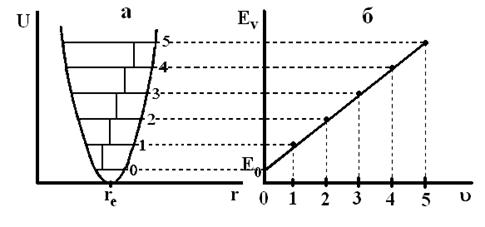
Рис.12. Кривая потенциальной энергии (а) и зависимость колебательной энергии Еν от ν (б) для гармонического осциллятора.
Модель гармонического осциллятора приводит к положениям, противоречащим реальным экспериментальным данным. Во-первых, Eν для гармонического осциллятора может быть сколь угодно большой. В этом случае химическая связь в молекуле была бы бесконечно упругой, и ее разрыв был бы невозможен. Мы знаем, что это не так. Во-вторых, для гармонического осциллятора в спектре поглощения должна наблюдаться только одна полоса, что вытекает из правил отбора и эквидистантности колебательных уровней (рис.12а). Однако в спектре реальной двухатомной молекулы наблюдается несколько полос (рис.10). Все это означает, что реальные молекулы не являются гармоническими осцилляторами. Гармоническое приближение для них можно использовать только при малых смещениях ядер от положения равновесия, или, что то же самое, при малых значениях колебательного квантового числа (ν = 0; l).
Тем не менее, модель гармонического осциллятора позволяет оценивать силовую постоянную и упругость химической связи. Кроме того, в некоторых случаях колебания реальных молекул в достаточно хорошем приближении можно считать гармоническими, особенно в твердых телах. Наконец, гармоническое приближение является на сегодняшний день наиболее распространенным при исследованиях колебательных спектров многоатомных молекул.
Для реальных двухатомных молекул функция U(r) не является параболой и возвращающая сила не строго пропорциональна величине смещения ядер. Это приводит к модели ангармонического осциллятора, для которого кривая потенциальной энергии описывается функцией Морзе (рис. 13):
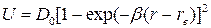 (44)
(44)
где D0-энергия диссоциации, b-постоянная для данной молекулы.
В этом случае колебательная энергия будет равна:
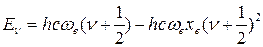 (45)
(45)
где ωехе – коэффициент ангармоничности, характеризующий отклонение колебаний от гармоничности, причем 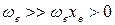 . Величина ωехе измеряется в тех же единицах, что и ωе (м-1, см-1). Безразмерную величину хе также иногда называют коэффициентом ангармоничности.
. Величина ωехе измеряется в тех же единицах, что и ωе (м-1, см-1). Безразмерную величину хе также иногда называют коэффициентом ангармоничности.
Из уравнения (45) можно получить выражение для колебательного терма:
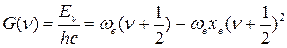 (46)
(46)
а также для нулевой энергии ангармонического осциллятора:
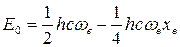 (47)
(47)
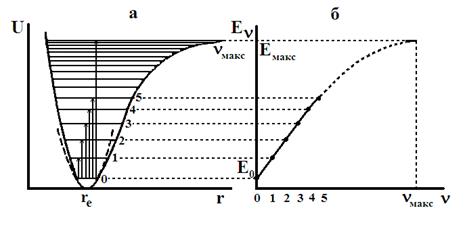
Рис. 13. Кривая потенциальной энергии (а) и зависимость колебательной энергии Еν от ν (б) для ангармонического осциллятора.
Кривая Еν-ν имеет максимум (рис.13б) и колебательные уровни сходятся к некоторому значению νмакс, которое можно найти из условия максимума: 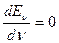
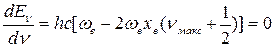 (48)
(48)
откуда
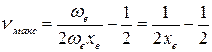 (49)
(49)
Таким образом, существует конечное число дискретных колебательных уровней и максимальная энергия ангармонического осциллятора Еν,макс. Если молекуле сообщить колебательную энергию Еν > Еν,макс, произойдет диссоциация, как это видно из кривой потенциальной энергии (рис.13а).
Рассчитанные по формуле (49) значения νмакс для большинства молекул составляют несколько десятков, для некоторых – до полутора сотен.
Следует отметить, что уравнение (45) недостаточно точно описывает зависимость Еν от ν, особенно при больших значениях ν. Причина – в приближенном характере функции Морзе, на основании, которой было получено уравнение (45). Отсюда вытекает и приближенный характер формулы (49), которая обычно дает завышенные значения νмакс.
Для уточнения уравнения (45) его нередко дополняют кубическим членом, содержащим второй коэффициент ангармоничности 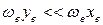 :
:
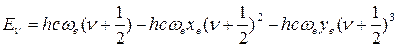 (50)
(50)
Для ангармонического осциллятора квантовомеханические правила отбора разрешают любые переходы: Δν = ±1, ±2, ±3 и т.д.
Для большинства двухатомных молекул колебательный переход 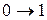 требует ~10-100 кДж/моль. Это значительно больше средней энергии теплового движения молекул газа при температуре опыта (18-250С) (RT
требует ~10-100 кДж/моль. Это значительно больше средней энергии теплового движения молекул газа при температуре опыта (18-250С) (RT 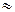 2,5 кДж/моль при 298 К), поэтому можно считать, что при этой температуре подавляющее число молекул находится на самом низшем колебательном уровне, т.е.
2,5 кДж/моль при 298 К), поэтому можно считать, что при этой температуре подавляющее число молекул находится на самом низшем колебательном уровне, т.е. 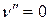 .
.
Наименьшая энергия требуется для перехода 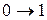 . Это соответствует появлению в спектре поглощения первой (низкочастотной) полосы – основного тона (см. рис.10). Переходы
. Это соответствует появлению в спектре поглощения первой (низкочастотной) полосы – основного тона (см. рис.10). Переходы 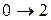 ,
, 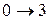 и т.д. дают последующие полосы – обертоны.
и т.д. дают последующие полосы – обертоны.
В общем виде уравнение для волновых чисел колебательных переходов с нулевого уровня на любой уровень ν будет следующим:
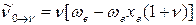 (51)
(51)
где ν = 1,2,3…νмакс.
С учётом этого, для волновых чисел основной полосы и первого и второго обертонов получаем:
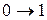 основная полоса (основной тон)
основная полоса (основной тон) 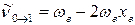
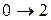 1-й обертон
1-й обертон 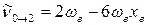
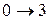 2-й обертон
2-й обертон 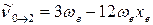
 Измерив волновые числа основного тона и 1-го обертона, можно вычислить собственную частоту колебаний и коэффициент ангармоничности, а затем и важную характеристику молекулы – энергию диссоциации.
Измерив волновые числа основного тона и 1-го обертона, можно вычислить собственную частоту колебаний и коэффициент ангармоничности, а затем и важную характеристику молекулы – энергию диссоциации.
Энергией диссоциации двухатомной молекулы называют изменение энергии ΔU0 (при абсолютном нуле) в результате перехода 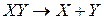 , причем и молекулы ХУ и атомы X и
, причем и молекулы ХУ и атомы X и 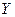 находятся в состоянии идеального газа. Продукты реакции должны быть удалены на бесконечно большое расстояние, а молекула
находятся в состоянии идеального газа. Продукты реакции должны быть удалены на бесконечно большое расстояние, а молекула 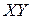 должна находиться на нулевом колебательном уровне (что согласуется с условием: Т=0).
должна находиться на нулевом колебательном уровне (что согласуется с условием: Т=0).
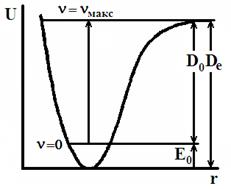
Энергию диссоциации, отсчитываемую от нулевого уровня и отнесенную к 1 молю двухатомного газа, называют истинной энергией диссоциации и обозначают D0:
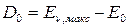 (52)
(52)
Если энергию диссоциации отсчитывать от минимума потенциальной кривой, то она превышает D0 на величину нулевой энергии
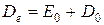 (53)
(53)
По колебательным спектрам поглощения можно рассчитать D0, а затем, зная Е0, найти Dе. Величину Е0, а, следовательно, и Dе, можно рассчитать только используя экспериментальные спектральные данные. Поэтому Dе часто называют спектроскопической энергией диссоциацией.
