Материально–техническое обеспечение. 1. Установка для лабораторной работы по электричеству и магнетизму «Исследование

1. Установка для лабораторной работы по электричеству и магнетизму «Исследование электростатического поля».

2. Программа для моделирования лабораторной работы на компьютере.

Лабораторная работа №14

«Определение удельного сопротивления проводника»

Краткая теория

Если линейный проводник длиной и площадью поперечного сечения изготовлен из однородного материала, то его сопротивления определяется по формуле

(1)

а сопротивление может быть экспериментально найдено из закона Ома:

, (2)

где – напряжение на концах исследуемого проводника, а – сила тока в проводника.

Для того, чтобы определить удельное сопротивление проводника, необходимо собрать электрическую цепь, схема которой изображена на рис.1.

Между точками «а» и «в» включена проволока из исследуемого материала. Если диаметр проволоки постоянен по всей длине, то площадь ее поперечного сечения

(3)

В данной работе мм

Их соотношений (1) – (3) для расчета удельного сопротивления 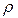получается расчетная формула:

(4)

Для проверки формулы (1), отражающей зависимость сопротивления проволоки от ее длины , определяют сопротивление проволоки по формуле (2) при разных длинах и строят график зависимости – (рис.2)

Поскольку проволока однородна ( ) и имеет одинаковое поперечное сечение по всей длине ( ), то экспериментальные точки должны ложиться на прямую, проходящую через начало координат (рис.2)

Порядок выполнения работы.

1. Собираем электрическую схему, показанную на рис.1

2. Измеряем ток и напряжение при длинах проволоки м

3. Данные измерения записываем в таблицу 1.

Протокол лабораторной работы №14

Таблица 1

	0,1	0,2
,В
,Ом

4. По данным измерениям рассчитываем 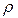по ф–ле (4) и определяем по формуле (1).

Вопросы для самопроверки к работе №14

1. Что такое электрический ток? Плотность тока?

2. Напишите формулу для сопротивления проводника.

3. Как зависит удельное сопротивление от температуры?

4. Чему равно сопротивление проводников при последовательном и параллельном сопротивлении?

5. Напишите закон Ома в дифференциальной форме; для участка цепи; для замкнутой цепи.

Список рекомендуемой литературы

1. Дмитриева В.Ф., Прокофьев В.Л. Основы физики. – М.: Высшая школа, 2009.

2. Трофимова Т.И. Курс физики. – М.: Высшая школа, 2010.

Материально–техническое обеспечение

Установка для лабораторной работы по электричеству и магнетизму «Определение удельного сопротивления проводника».

Лабораторная работа № 15

«Определение напряжённости магнитного поля Земли

с помощью тангенс–гальвонометра»

Краткая теория

Магнитное поле образуется вокруг любого движущегося заряда, в частности вокруг проводника с током.

Свойства магнитного поля, образованного движущимся зарядами тождественны свойствам магнитного поля вокруг постоянных магнитов.

Основной характеристикой магнитного поля является вектор магнитной индукции , направление которого совпадает с касательными к магнитным силовым линиям.

Магнитные силовые линии поля, образованного проводником с током,

представляют собой концентрические окружности, которые лежат в плоскостях, перпендикулярных проводнику с током, с центром на проводнике. (см. рис.1). Направление силовых линий определяется правилом буравчика.

Физический смысл вектора , определяется из закона Ампера: на проводник с током , помещенный в магнитное поле, действует сила, равная:

(1)

– векторная запись закона Ампера, или

(2)

– скалярная запись. При (т.е. если магнитное поле однородно) закон Ампера можно записать так:

, откуда, при условии ,

, (3)

т.е. вектор магнитной индукции определяется силой, действующей на проводник единичной длины, по которому течет ток силой в 1А.

Единицей измерения служит Тл (тесла), размерность которой определяется из формулы (3): .

Численное значение вектора магнитной индукции определяется из закона Био–Савара–Лапласа (для элемента тока dl). В векторной форме , в скалярной записи – (4)

где r– расстояние от элемента тока dl до т.А, где определяется элементарное значение dB магнитного поля, – угол между dl и r (рис. 1а);

– магнитная проницаемость среды; – магнитная постоянная.

Часто магнитное поле изучается в воздухе или вакууме и тогда рациональнее использовать для описания поля не , а вектор напряженности , который равен: , т.е. не зависящий от магнитных свойств среды.

Тогда закон Био–Савара–Лапласа для dH запишется в виде:

; (5)

Используя формулу (5) можно найти напряженность магнитного поля, образованного проводником с током любой конфигурации. Например, магнитное поле, образованное круговым током, описывается вектором , который в центре кругового тока направлен перпендикулярно плоскости круга. Численное значение получим, если учесть, что , .

; (рис 2).

Если поле образовано n– витками с током, то:

;

В случае, если поле образовано очень большим количеством витков N с током, намотанным на очень длинный каркас (т.е. образует соленоид), то для нахождения напряженности внутри соленоида используют закон полного тока: ; с другой стороны: , тогда и , где N– полное число витков соленоида, – его длина; n– число витков соленоида на единице длины.

В любой точке над поверхностью Земли обнаруживается действие магнитных сил, земной магнетизм. В настоящее время существуют две гипотезы земного магнетизма:

1. Гипотеза, объясняющая наличие магнитного поля электрическими токами, циркулирующими на больших глубинах в жидком ядре Земли.

2.Гипотеза, основанная на предложении, что земная кора содержит в разных участках различное количество магнитных пород. Происхождение магнитного поля окончательно еще не выяснено.

Цель работы – определить горизонтальную составляющую магнитного поля Земли.