Материально–техническое обеспечение. 1. Установка для лабораторной работы по электричеству и магнетизму «Определение
1. Установка для лабораторной работы по электричеству и магнетизму «Определение напряженности магнитного поля Земли с помощью тангенс–гальванометра»
2. Программа для моделирования лабораторной работы на компьютере.
Модуль 4.Оптика
Лабораторная работа №24
«Определение длины световой волны при помощи дифракционной решетки»
Краткая теория
Дифракция света
Развитие оптики вплоть до начала XX века базировалось в основном, на представлении о прямолинейности распространения света. Но уже в XVII веке были известны факты, указывающие на отступление от закона прямолинейного распространения. Это бывает в следующих случаях: когда луч света проходит через малое отверстие в непрозрачном экране; если на пути луча находится малое непрозрачное тело и если свет проходит около края непрозрачного предмета.
Если пучок параллельных лучей света встречает на своем пути непрозрачное круглое тело, то при достаточно малых размерах тела на экране, в середине геометрической тени, будет заметно с в е т л о е пятно в центре чередующихся темных и светлых колец. Это указывает на то, что свет распространяется и в область геометрической тени.
Если же пучок параллельных лучей света пропустить через достаточно малое круглое отверстие, то на экране, начиная с некоторого расстояния, по мере изменения расстояния между отверстием и экраном, будет появляться то с в е т л о е пятно, то т е м н о е пятно в центре чередующихся темных и светлых колец, диаметр которых значительно больше диаметра отверстия. Свет здесь распространяется в область геометрической тени.
Явление отклонения света от прямолинейного распространения в однородной среде, выражающееся в распространении света в область геометрической тени, называется д и ф р а к ц и е й света.
Дифракция света показывает, что законы геометрической оптики, базирующиеся на законе прямолинейности распространения света, так же как и ряд других законов физики, оказываются справедливыми только в известных условиях.
Принцип Гюйгенса
Направление распространения света в области геометрической тени можно определить при помощи метода, получившего название принцип Гюйгенса, который объясняет механизм передачи волнового процесса (рис.1а). Гюйгенс рассматривал распространение световых волн как последовательное возмущение точек среды, в которой распространяется свет. По принципу Гюйгенса каждая точка волновой поверхности (фронта волны) является самостоятельным источником вторичных элементарных сферических волн. Поверхность, огибающая эти вторичные волны, является новой волновой поверхностью (фронтом волны). В изотропной среде световые лучи являются нормалями волновой поверхности.
Но принцип Гюйгенса позволил решать задачи распространения светового фронта, не отвечая на вопрос об интенсивности волн, идущих по разным направлениям. Оставался нерешенным и вопрос о прямолинейности распространения света. Эти недостатки принципа Гюйгенса устранил Френель, который дополнил принцип Гюйгенса идеей интерференции волн.
Принцип Гюйгенса – Френеля
Огибающая поверхность вторичных элементарных волн Гюйгенса рассматривается Френелем как поверхность, где вследствие взаимной интерференции элементарных волн результирующая волна имеет заметную интенсивность. При определении интенсивности (амплитуды) результирующей волны Френель предложил рассматривать поверхность фронта волны S как светящуюся поверхность. Излучение отдельных элементов dS поверхности S (рис. 1а) приходя в точку Е определяет своей совокупностью интенсивность излучения в этой точке. Так как фазы всех источников dS определяются излучением, идущим из точки О, то они будут когерентными и при сложении в точке Е будут интерферировать. Для вычисления интенсивности результирующей волны Френель предложил следующий прием, получивший название метода зон Френеля.
Метод зон Френеля
Соединим источник света О с рассматриваемой точкой М (рис.1б), разбиваем поверхность SS фронта волн на зоны такого размера, чтобы расстояние l от краев зоны до М отличались на полволны, т.е. радиусами:
l0 = в; l1 = в + 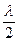 ; l2 = в + 2
; l2 = в + 2 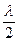 ; l3 = в +
; l3 = в + 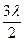 ... ln = в +
... ln = в + 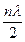 .
.
Если пренебречь малыми величинами второго порядка, то площади каждой полученной зоны будут одинаковыми и равны
DS = 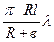 , а радиус n–ой зоны , а радиус n–ой зоны 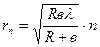 | (1) |
При этом необходимо учитывать следующие обстоятельства:
1. По мере удаления от центра С нормаль к волновой поверхности составляет все больший угол с направлением СМ и вследствие этого действие удаленных зон будет мало эффективным.
2. При построении зон по методу Френеля соответствующие точки двух соседних зон будут отличаться по фазе на p и при интерференции в точке М будут гасить друг друга.
Математические вычисления показывают, что действие безграничной световой поверхности S в точке М сводится к эквивалентному действию половины одной центральной зоны. Этим и объясняется прямолинейность распространения света.
Вопрос о том, что будет наблюдаться в точке М, максимум или минимум интенсивности от света, проходящего через отверстие SS, решается числом зон Френеля, которые укладываются в отверстии.
1. Если число зон будет четное, то зоны попарно погасят друг друга и в точке М будет минимум интенсивности.
2. Если число зон Френеля будет нечетное, то парные зоны погасят друг друга, а одна зона остается не погашенной и даст максимум интенсивности.
Дифракцию света, наблюдаемую от сферических волн, т.е. в случае, когда источник света находится на конечном расстоянии R, называют дифракцией Френеля.
Дифракцию света, наблюдаемую от параллельных лучей, т.е. в случае, когда источник света находится в бесконечности и фронт волны плоский, называют дифракцией Фраунгофера.
Если фронт волны плоский, то R = 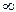 и площади DSi, будут равны DS = pbl, а радиусn–ой зоны Френеля
и площади DSi, будут равны DS = pbl, а радиусn–ой зоны Френеля
rn =  | (2) |
