Предмет классической электродинамики

ЭЛЕКТРИЧЕСТВО

И ЭЛЕКТРОМАГНЕТИЗМ

Курс лекций по физике

для студентов инженерно-технических

специальностей

ЭЛЕКТРОСТАТИКА

Лекция 1. Электрическое поле в вакууме

План лекции

1.1. Предмет классической электродинамики.

1.2. Электростатика. Закон Кулона. Напряженность.

1.3. Теорема Гаусса для электростатического поля и ее применение к расчету электростатических полей.

Предмет классической электродинамики

Еще в глубокой древности были известны опыты по электризации трением (сам термин появился позднее) и особенности силового взаимодействия тел после электризации (притяжение и отталкивание). Было установлено, что существуют только два типа электрических зарядов, названных условно положительными и отрицательными, и что заряды одного знака отталкиваются, разноименные – притягиваются. К этой (в основном качественной) информации с конца восемнадцатого века начали добавляться выявленные количественные соотношения и закономерности, определяющие электрические явления.

Было установлено, что электрический заряд дискретен, то есть заряд любого тела составляет целое кратное от элементарного электрического заряда «е» (е = 1,6·10¹⁹ Кл). Элементарные частицы: электрон и протон являются соответственно носителями элементарных отрицательного и положительного заряда. Обобщение опытных данных позволило сформулировать закон сохранения заряда: алгебраическая сумма зарядов любой замкнутой системы (не обменивающейся зарядами с внешними телами) остается неизменной. Оказалось, что электрические заряды инвариантны к преобразованиям координат, т.е. не зависят от системы отсчета. Единица электрического заряда в «СИ» – 1 Кулон (производная единица, определяемая через силу тока) – это заряд, проходящий через поперечное сечение проводника за одну секунду при силе тока в 1А.

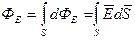
1.2. Электростатика. Закон Кулона.
Напряженность

В 1785 году французским ученым Ш.Кулоном[1] был установлен закон взаимодействия неподвижных точечных зарядов (размеры которых малы по сравнению с расстояниями до других зарядов): сила взаимодействия F между двумя точечными зарядами Q₁, и Q₂ пропорциональна величинам зарядов и обратно пропорциональна квадрату расстояния между ними.

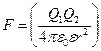, (1.1)

здесь 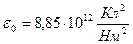– электрическая постоянная; 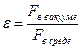– диэлектрическая проницаемость среды – безразмерная величина, показывающая во сколько раз сила взаимодействия между зарядами в вакууме ослабляется данной средой (для примера: диэлектрическая проницаемость парафина равна 2; слюды – 6, этилового спирта – 25; дистиллированной воды – 81; воздуха – 1,0003 ≈ 1,0). Кулоновская сила 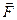направлена по прямой, соединяющей заряды, то есть является центральной и соответствует притяжению в случае разноименных зарядов и отталкиванию в случае – одноименных зарядов.

В векторной форме закон Кулона имеет вид:

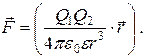(1.1а)

Если в пространство, окружающее электрический заряд, внести другой заряд, то на него будет действовать кулоновская сила, то есть в пространстве вокруг заряда существует силовое поле. В данном случае говорят об электрическом поле, посредством которого взаимодействуют электрические заряды.

Рассмотрим электрические поля, которые создаются неподвижными зарядами и которые называются электростатическими. Если в некоторую точку А поля, создаваемого зарядом Q, помещать поочередно заряды Q₁; Q₂;… Q_n и определять значения кулоновской силы: 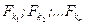, то согласно (1.1) и, это подтверждается экспериментом, отношение 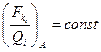. Эта величина принята в качестве силовой характеристики электростатического поля и называется напряженностью

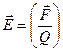, (1.2)

Из (1.2) следует, что при Q = 1 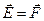, то есть напряженность электростатического поля в данной точке определяется силой действующей на единичный положительный заряд, помещенный в эту точку поля. В соответствии с (1.1) и (1.2) напряженность поля точечного заряда можно находить по формуле

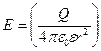(1.3)

Направление вектора 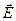совпадает с направлением силы, действующей на положительный заряд. Размерность напряженности в СИ – .

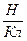В векторном виде: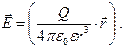

Графически электростатическое поле изображают с помощью линий напряженности – линий, касательные к которым в каждой точке совпадают с направлением вектора 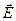в этой точке. Так как в каждой данной точке пространства вектор 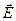имеет только одно направление, то линии напряженности никогда не пересекаются. Чтобы с помощью линий напряженности можно было характеризовать не только направление, но и величину напряженности электростатического поля, их проводят с определенной густотой: число линий напряженности dN пронизывающих единицу площади поверхности dS,перпендикулярную линиям напряженности, должно быть равно числовому значению вектора 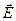. Если приписать величине 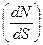размерность

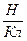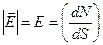Е , то (1.4)

В качестве примера на (рис.1.1) представлено графическое изображение (с помощью линий 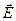) электростатических полей: положительного точечного заряда ("а"); отрицательного точечного заряда ("б"); двух точечных зарядов ("в") и поля двух параллельных равномерно заряженных разноименными зарядами плоскостей ("г").

Рис.1.1

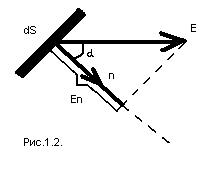
Электростатическое поле также характеризуется скалярной величиной, называемой поток вектора напряженности сквозь рассматриваемые поверхности Ф_Е. Элементарный поток вектора 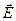сквозь площадку dS вводится как скалярное произведение по формуле

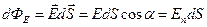' (1.5)

(см.. рис.1.2), здесь dS – площадь элементарной площадки, 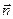– единичный вектор нормали к площадке; 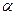– угол между векторам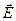и и 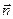; 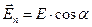– проекция вектора Е на направление 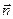; 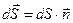– условный вектор, модуль которого равен площади dS, а направление совпадает с " ".

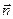Поток Ф_E через конечную поверхность S определяется, как

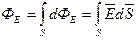(1.6)

Из выражений (1.5, 1.6) следует, что знак Ф_E зависит от знака cos 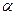, который в свою очередь зависит от взаимного расположения векторов 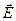и .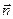

Направление 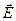задается расположением электрических зарядов, а за направление 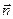для замкнутой поверхности S – направление нормали, выходящей из области, охватываемой замкнутой поверхностью S. Таким образом, поток вектора 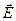напряженности электростатического поля сквозь рассматриваемую поверхность S пропорционален числу линий вектора 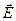, пронизывающих эту поверхность.

Рис.1.2

Рассмотрим электростатическое поле, создаваемое системой неподвижных точечных зарядов Q₁; Q₂;… Q_n, в некоторой точке которого находится заряд Q. Эксперимент показывает, что для кулоновских сил справедлив, действующий в механике принцип независимости действия сил – результирующая сила 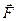, действующая со стороны поля на заряд Q, равна векторной сумме сил 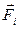, приложенных к нему со стороны каждого из зарядов Q_i:

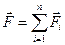(1.7)

Согласно (1.2) 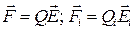, где 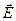– напряженность результирующего поля; 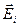– напряженность поля заряда Q_i. Подставляя эти выражения в (1.7) получим соотношение

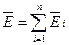, (1.8)

выражающее принцип суперпозиции (наложения) электростатических полей: напряженность поля системы неподвижных точечных зарядов в некоторой точке равна векторной сумме напряженностей полей, создаваемых в этой точке каждым из зарядов в отдельности. Принцип суперпозиции позволяет рассчитывать электростатические поля любой системы неподвижных зарядов так как, если заряды не точечные, то их всегда можно свести к совокупности точечных зарядов.