Методика проведения работы
Метод определения 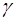 , который используется в данной работе, носит название метода Клемана-Дезорма. При вы-полнении работы с некоторым количеством воздуха про-исходят термодинамические процессы, графики которых в координатах
, который используется в данной работе, носит название метода Клемана-Дезорма. При вы-полнении работы с некоторым количеством воздуха про-исходят термодинамические процессы, графики которых в координатах 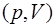 представлены на рис.1.2.3.
представлены на рис.1.2.3.
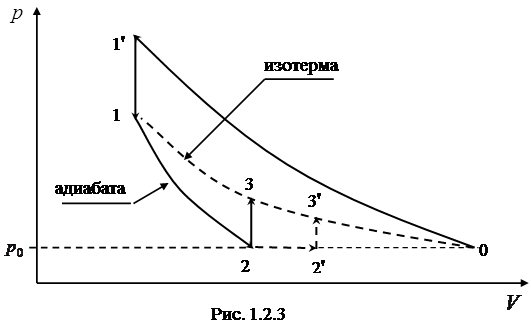 |
На рис.1.2.3 точка 0 соответствует состоянию, при ко-тором некоторое количество воздуха с массой 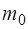 имеет параметры
имеет параметры 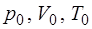 . Давление
. Давление 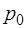 и температура
и температура 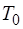 совпа-дают с давлением и температурой окружающей среды (ат-мосферного воздуха). При нагнетании воздуха в баллон на-сосом происходит процесс 0-1'. Воздух при этом сжимается и немного нагревается. Далее в течение 2-3 минут воздух в баллоне охлаждается до температуры окружающей среды
совпа-дают с давлением и температурой окружающей среды (ат-мосферного воздуха). При нагнетании воздуха в баллон на-сосом происходит процесс 0-1'. Воздух при этом сжимается и немного нагревается. Далее в течение 2-3 минут воздух в баллоне охлаждается до температуры окружающей среды 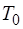 (процесс 1'-1). В состоянии 1 воздух массой
(процесс 1'-1). В состоянии 1 воздух массой 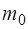 в баллоне имеет параметры
в баллоне имеет параметры 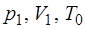 .
.
Давление 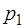 при этом равно:
при этом равно:
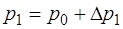 ;
; 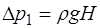 , (1.2.37)
, (1.2.37)
где 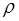 – плотность жидкости в манометре;
– плотность жидкости в манометре;
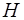 – разность высот уровней поверхности жидкости в коленах манометра в состоянии 1.
– разность высот уровней поверхности жидкости в коленах манометра в состоянии 1.
Если открыть кран, закрывающий воздух в баллоне, до давление воздуха так быстро уменьшится до 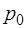 , что рас-ширение воздуха, соответствующее процессу 1-2, можно считать адиабатическим.
, что рас-ширение воздуха, соответствующее процессу 1-2, можно считать адиабатическим.
Если в состоянии 2 перекрыть краном трубку, соединя-ющую воздух в баллоне с атмосферным воздухом, то в ре-зультате теплообмена воздух в баллоне изохорически наг-ревается до температуры 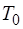 (процесс 2-3). В состоянии 3 давление воздуха равно:
(процесс 2-3). В состоянии 3 давление воздуха равно:
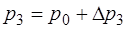 ;
; 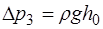 , (1.2.38)
, (1.2.38)
где 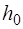 – разность высот уровней жидкости в манометре в состоянии 3.
– разность высот уровней жидкости в манометре в состоянии 3.
Если в формулу (1.2.28) подставить 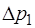 и
и 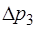 , определя-емые формулами (1.2.37) и (1.2.38), то получим:
, определя-емые формулами (1.2.37) и (1.2.38), то получим:
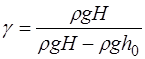 . (1.2.39)
. (1.2.39)
После сокращений в формуле (1.2.39) расчетная формула для определения 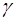 принимает вид
принимает вид
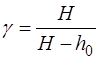 . (1.2.40)
. (1.2.40)
Величину 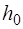 мы измерим точно, если, наблюдая процесс 1-2, перекроем кран в то мгновение, когда воздух в баллоне окажется в состоянии 2. Для данной экспериментальной ус-тановки время процесса 1-2 составляет несколько десятых долей секунды. Запаздывание с перекрытием крана приво-дит к тому, что начинается изобарическое нагревание воз-духа в баллоне (процесс 2-2') и величина
мы измерим точно, если, наблюдая процесс 1-2, перекроем кран в то мгновение, когда воздух в баллоне окажется в состоянии 2. Для данной экспериментальной ус-тановки время процесса 1-2 составляет несколько десятых долей секунды. Запаздывание с перекрытием крана приво-дит к тому, что начинается изобарическое нагревание воз-духа в баллоне (процесс 2-2') и величина 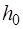 определяется неточно. Мы получим заниженное значение
определяется неточно. Мы получим заниженное значение 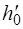 . Если же кран закрыть раньше, то мы получим завышенное значение
. Если же кран закрыть раньше, то мы получим завышенное значение 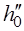 (рис.1.2.4).
(рис.1.2.4).
 |
Поскольку время процесса 1-2 составляет несколько де-сятых долей секунды, что сравнимо со временем челове-ческой реакции, то при проведении эксперимента чаще все-го будут получаться заниженные значения 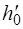 , причем зани-жение будет тем значительнее, чем дольше будет открыт выпускной кран. Найдем зависимость между
, причем зани-жение будет тем значительнее, чем дольше будет открыт выпускной кран. Найдем зависимость между 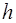 – разностью высот уровней жидкости в манометре в состоянии 3 и
– разностью высот уровней жидкости в манометре в состоянии 3 и 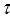 – временем изобарного нагревания.
– временем изобарного нагревания.
При изобарном нагревании количество теплоты, сооб-щенное воздуху в баллоне, пропорционально разности тем-ператур воздуха 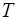 и окружающей среды
и окружающей среды 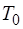 , а также проме-жутку времени
, а также проме-жутку времени 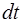 , в течение которого происходит нагрева-ние:
, в течение которого происходит нагрева-ние:
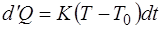 , или
, или 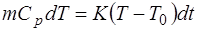 , (1.2.41)
, (1.2.41)
где 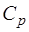 – удельная теплоемкость воздуха при
– удельная теплоемкость воздуха при 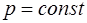 ;
;
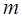 – масса воздуха;
– масса воздуха;
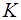 – коэффициент теплопередачи, отнесенный к пол-ной площади поверхности баллона.
– коэффициент теплопередачи, отнесенный к пол-ной площади поверхности баллона.
Разделяя переменные в уравнении (1.2.41):
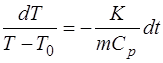
интегрируем, пренебрегая зависимостью массы 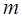 от темпе-ратуры
от темпе-ратуры 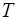 :
:
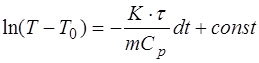 , (1.2.42)
, (1.2.42)
где 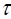 – время изобарического нагревания. Постоянную интегрирования в уравнении (1.2.42) определяют из начального условия:
– время изобарического нагревания. Постоянную интегрирования в уравнении (1.2.42) определяют из начального условия: 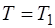 при
при 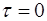 . Определив постоян-ную и потенцируя уравнение (1.2.42), найдем
. Определив постоян-ную и потенцируя уравнение (1.2.42), найдем
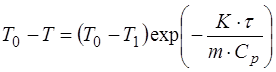 ,
,
или после деления на 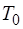 получим
получим
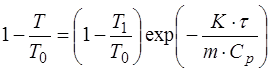 . (1.2.43)
. (1.2.43)
При изохорическом нагревании (процесс 2-3) отношение  , т.е. получаем равенство
, т.е. получаем равенство
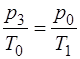 , или
, или 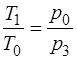 .
.
Отсюда
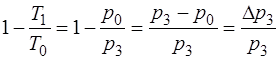 . (1.2.44)
. (1.2.44)
При изохорическом нагревании (процесс 2'-3') анало-гично получаем:
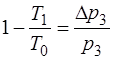 , (1.2.45)
, (1.2.45)
где
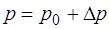 ;
; 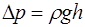 . (1.2.46)
. (1.2.46)
Подставляя формулы (1.2.44) и (1.2.45) в формулу (1.2.43), получим с учетом формул (1.2.38) и (1.2.46):
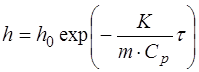 . (1.2.46)
. (1.2.46)
При выводе (1.2.46) учтено, что 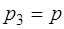 (различие состав-ляет несколько десятых долей процента).
(различие состав-ляет несколько десятых долей процента).
Логарифмируя (1.2.46) по основанию е, получим уравне-ние
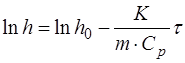 , (1.2.47)
, (1.2.47)
описывающее искомую зависимость 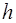 от
от 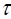 . На рис.1.2.5 представлен график зависимости
. На рис.1.2.5 представлен график зависимости 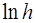 от
от 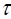 . Видно, что, пов-торив опыт несколько раз с различным временем запазды-вания можно
. Видно, что, пов-торив опыт несколько раз с различным временем запазды-вания можно 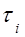 , можно, зная значения
, можно, зная значения 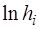 , найти путем экстраполяции величины
, найти путем экстраполяции величины 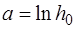 и
и 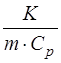 . Тогда
. Тогда
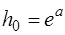 . (1.2.48)
. (1.2.48)
 |
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Включить электрическую схему экспериментальной ус-тановки с помощью тумблеров "СЕТЬ" и "КОМПРЕССОР". Зафиксировать начальный уровень жидкости в манометре.
2. Нажать клапан "НАПУСК", открывающий кран K1 и включающий насос, и накачать воздух в баллон так, чтобы жидкость в трубке манометра опустилась на 8-10 см от на-чального уровня. При этом разность уровней в трубках манометра равна 16-20 см.
3. Отпустить клапан "НАПУСК", закрывая кран K1. Че-рез 2-3 минуты произвести дополнительную регулировку до заданного уровня. Измерить разность 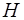 уровней жидкости в манометре. В дальнейших опытах заданный уровень
уровней жидкости в манометре. В дальнейших опытах заданный уровень 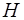 необходимо поддерживать постоянным.
необходимо поддерживать постоянным.
4. Быстро нажать на клапан "СБРОС", открывающий кран K2, и одновременно включить секундомер. Выдержать кран К2 открытым в течение заданного времени 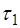 . После этого отпустить клапан "СБРОС", закрывая К2, и оста-новить секундомер. Через 2-3 минуты, когда давление в баллоне перестанет меняться, измерить разность
. После этого отпустить клапан "СБРОС", закрывая К2, и оста-новить секундомер. Через 2-3 минуты, когда давление в баллоне перестанет меняться, измерить разность 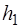 уровней жидкости в манометре.
уровней жидкости в манометре.
5. Повторить пункты 2-4 для другого времени 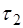 и изме-рить
и изме-рить 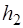 . Опыты нужно выполнять для
. Опыты нужно выполнять для 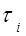 = 5,10,15,20,25,30 секунд, опреде-ляя каждый раз значения
= 5,10,15,20,25,30 секунд, опреде-ляя каждый раз значения 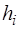 .
.
6. Результаты измерений занести в таблицу 1.
Таблица 1
| № п.п. | 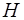 , см , см | 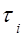 , с , с | 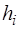 , см , см | 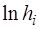 |
По результатам измерений 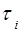 и
и 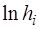 найти
найти 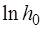 и абсо-лютную погрешность (полуширину доверительного интер-вала)
и абсо-лютную погрешность (полуширину доверительного интер-вала) 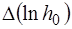 . Величина
. Величина 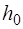 соответствует мгновенному (адиа-батическому) расширению воздуха. Согласно уравнению (1.2.47) график функции
соответствует мгновенному (адиа-батическому) расширению воздуха. Согласно уравнению (1.2.47) график функции 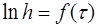 – прямая линия. Прибли-женно
– прямая линия. Прибли-женно 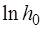 и
и 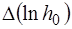 можно найти по графику (см. рис. 1.2.5).
можно найти по графику (см. рис. 1.2.5).
Более точные результаты дает применение метода наи-меньших квадратов. Если ввести обозначения
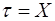 ;
; 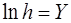 ;
; 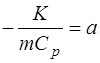 ,
, 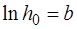 ,
,
то уравнение (1.2.47) можно записать в виде уравнения пря-мой:
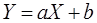 .
.
Методика применения метода наименьших квадратов и расчета погрешностей приведены в Приложении 2
7. Определить h0 и абсолютную погрешность 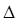 h0 по фор-мулам:
h0 по фор-мулам:
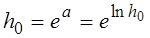 ;
; 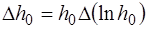 . (1.2.49)
. (1.2.49)
8. Найти отношение теплоемкостей воздуха 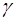 по формуле (1.2.40)
по формуле (1.2.40)
9. Определить абсолютную погрешность 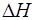 и вычислить абсо-лютную погрешность
и вычислить абсо-лютную погрешность 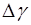 с помощью формулы
с помощью формулы
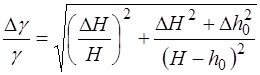 . (1.2.50)
. (1.2.50)
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое теплоёмкость?
2. Запишите уравнение Первого начала термодинамики.
3. Почему теплоемкость газов зависит от условий нагре-вания?
4. Почему 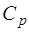 больше, чем
больше, чем 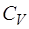 ?
?
5. Какой процесс называется адиабатическим?
6. Почему процесс выпуска воздуха может считаться ади-абатическим, несмотря на то, что веществ, не проводящих тепло, в природе не существует?
7. Какая система частиц называется идеальным газом?
8. Может ли газ в данной работе считаться идеальным и почему?
9. Запишите уравнение адиабатического процесса для иде-ального газа.
10. Что такое политропические процессы?
11. Каков смысл показателя политропы?
12. Какие изопроцессы Вы знаете? Запишите уравнения для каждого из них.
13. Запишите уравнение политропы для идеального газа.
14. Какие значения имеет показатель политропы при раз-личных изопроцессах?
15. Что происходит с внутренней энергией и температу-рой при адиабатическом процессе?
16. Что такое макро- и микросостояния системы?
17. Что такое статистический вес макросостояния?
18. Какое макросостояние называется равновесным?
19. Какой процесс называется необратимым?
20. Какой процесс называется квазистатическим?
21. Что такое степень свободы тела?
22. Какое число степеней свободы имеет двухатомная мо-лекула?
23. Как связано число степеней свободы молекул газа с теплоёмкостью этого газа?
24. Как связано число степеней свободы молекул газа с кинетической энергией этого газа?
25. Какая величина характеризует внутреннюю энергию газа?
26. Что такое связанная энергия? Как она передается?
27. Что такое энтропия? Каков статистический смысл эн-тропии?
28. Каков термодинамический смысл энтропии?
29. Как изменяется энтропия при адиабатическом процессе?
30. В расчетах используются формулы для постоянной массы газа. Как это согласовать с изменением массы газа в баллоне во время цикла, применяемого в работе?
