Исследование свободных колебаний в колебательном контуре
Принадлежности : лабораторный стенд с колебательным контуром, осциллограф.
Краткая теория
Колебательный контур - это замкнутая электрическая цепь, состоящая из катушки индуктивности (L) и конденсатора (С) (рис.1).
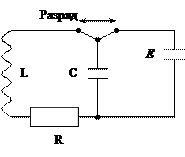 |
Рис. 1
Активное сопротивление (R) специально не включают в контур, но оно всегда присутствует и состоит из сопротивления проводов и эквивалентно потерям энергии в контуре. Если любым способом (например, зарядив конденсатор) запасти энергию в контуре и затем отключить контур от источников, то конденсатор начнет разряжаться. Изменяющийся ток разряда вызывает появление в катушке ЭДС самоиндукции, которая (по правилу Ленца) будет поддерживать ток разряда. Вследствие этого конденсатор не только разрядится до нуля, но и перезарядится. После чего процесс разряда повторяется в противоположном направлении.
Электромагнитные колебания - процесс периодического изменения заряда на конденсаторе, а, следовательно, и тока в контуре; он осуществляется за счет перехода энергии электрического поля конденсатора в энергию магнитного поля катушки и наоборот. При этом часть энергии этого колебательного процесса выделяется на сопротивлении в виде джоулева тепла, что и приводит к постепенному уменьшению запасенной энергии, заряда конденсатора и тока в контуре. Такие колебания называются затухающими.
На основании II закона Кирхгофа для рассматриваемого контура можно записать:
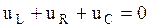 | или | 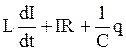 = 0 = 0 | (1) |
Здесь: 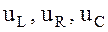 - напряжение на элементах контура L, R и C соответственно; I - ток в контуре; q - заряд конденсатора.
- напряжение на элементах контура L, R и C соответственно; I - ток в контуре; q - заряд конденсатора.
Решением этого уравнения будет выражение:
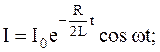 | 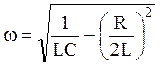 | (2) |
Графически эта зависимость представлена на рис. 2:
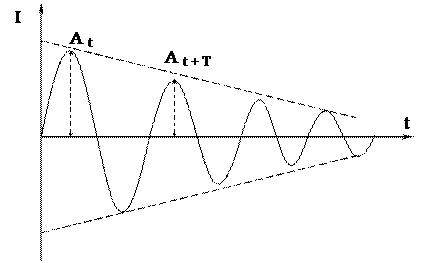 |
Рис. 2
При R = 0 колебания будут незатухающими, а
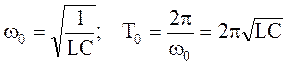 (формула Томсона) (формула Томсона) | (3) |
Здесь: ω0 и Т0 - частота и период свободных колебаний.
В реальном контуре величина 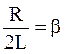 называется коэффициентом затуханий. Амплитуда тока
называется коэффициентом затуханий. Амплитуда тока 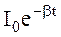 экспоненциально убывает во времени.
экспоненциально убывает во времени.
Логарифм отношения двух соседних амплитуд, разделенных во времени периодом колебаний, называется логарифмическим декрементом затухания(D) (рис. 2):
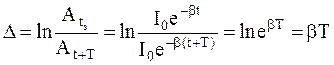 | (4) |
Добротность контура определяется с помощью соотношения:
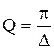 | (5) |
Цель работы: изучение затухающих колебаний тока в контуре на экране осциллографа, определение периода и логарифмического декремента затухания колебаний.
Описание установки
Установка состоит из лабораторного стенда и осциллографа. Измерительная схема установки представлена на рис. I. Колебательный контур состоит из катушки, индуктивность которой равна 0,01Гн и трех конденсаторов (С1, С2, С3), которые с помощью переключателя II поочередно включаются в контур, что позволяет изменять его частоту и период (ω1, ω 2, ω 3, и Т1, Т2, Т3 соответственно). Свободные колебания возбуждаются путем заряда конденсатора от выпрямителя. Трехэлектродная лампа в схеме выполняет роль ключа, который на одну половину периода переменного тока сети (S = 50Гц, Т = 0,02c) подключает контур к выпрямителю, на другую - отключает. За время второй половины периода возникают свободные затухающие колебания, которые наблюдаются на экране осциллографа.
