Скорости молекул газа (распределение Максвелла)

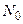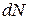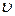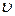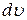Если - число молекул в каком–либо объеме газа, а - число молекул со скоростями от до ( + ), то

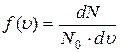- доля молекул, движущихся со скоростью .

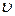Вид функции 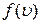был установлен Д.Максвеллом,

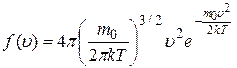(13)

и она носит название «функция Максвелла» (или функция распределения молекул по скоростям). График функции представлен на рисунке 1.

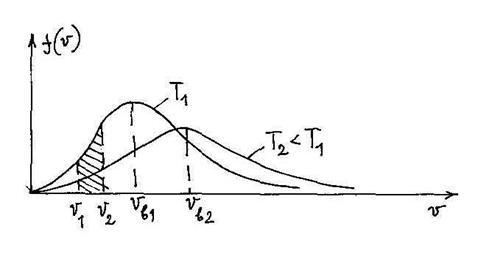Рисунок 1.

Свойства функции Максвелла:

· площадь, ограниченная функцией Максвелла 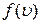и горизонтальной осью 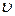, равна единице

· наиболее вероятная скорость молекул газа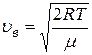

· средняя арифметическая скорость молекул определяется через функцию Максвелла

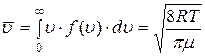
· доля молекул со скоростями от 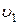до 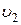численно равна площади заштрихованного участка на рисунке 1 и вычисляется через функцию Максвелла,

.

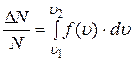Газ в поле тяжести (распределение Больцмана)

В поле тяжести, вызывающем ускорение свободного падения 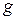, концентрация 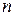газа убывает при увеличением высоты на = ,

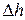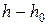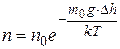, (14)

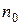- концентрация газа на высоте .

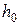Уравнение (14) строго выполняется, если только температура 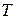газа не меняется с высотой.

Т.к. давление 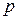и концентрация 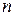связаны ( 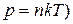, то уравнение, аналогичное уравнению (14), можно записать и для давлений. Если вести отсчет от уровня земли, т.е. считать на поверхности земли 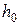=0, то давление газа на высоте 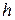описывается барометрической формулой

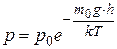, (15)

или

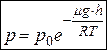, (16)

т.к. .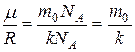

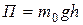представляет собой потенциальную энергию молекулы в поле тяжести Земли. Концентрация убывает с увеличением потенциальной энергии,

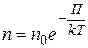. (17)

Уравнение (17) описывает изменение концентрации частиц в любом поле консервативных сил (не только сил тяжести). Уравнения (14) и (17) представляют собой распределение Больцмана.

ЯВЛЕНИЯ ПЕРЕНОСА.

К явлениям переноса относятся диффузия, теплопроводность и внутреннее трение (вязкость). Эти явления обусловлены хаотичным тепловым движением молекул и являются необратимыми.

Диффузия – самопроизвольное перемешивание частиц соприкасающихся веществ, или одного вещества, при котором выравнивается плотность . Уравнение диффузии (уравнение Фика)

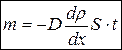, (18)

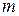- масса вещества, которая переносится через площадку 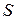за время 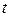в направлении x, перпендикулярном площадке. 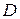- коэффициент диффузии, зависящий от рода вещества и температуры, 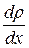- градиент плотности. Знак минус в уравнении отражает то, что перенос массы происходит в направлении меньшей плотности .

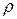Теплопроводность – перенос теплоты 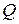в результате соударений молекул и передачи ими друг другу своей кинетической энергии. Уравнение теплопроводности (уравнение Фурье)

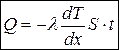, (19)

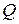– теплота, которая переносится через площадку 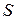за время 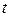в направлении x, перпендикулярном площадке; 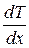- скорость изменения температуры в этом направлении; 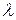- коэффициент теплопроводности материала. Перенос тепла происходит в область с меньшей температурой.

Внутреннее трение (вязкость) – сцепление между собой слоев жидкости или газа. При этом слои, движущиеся с разными скоростями, за счет соударений молекул передают друг другу импульс 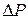, что приводит к выравниванию скорости 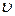движения слоев. Сцепление между собой слоев приводит к появлению сил трения между ними. За счет сил трения быстро движущийся слой замедляет свое движение, а медленно движущийся – убыстряет.

Уравнение внутреннего трения:

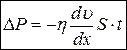, (20)

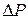- импульс, который переносится молекулами через площадку 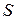за время 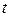в направлении 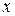, перпендикулярном скорости движения слоев. 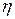- коэффициент вязкости, зависящий от рода жидкости или газа и их температуры.

Т.к. 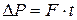, то сила трения между слоями жидкости или газа, действующая на площадь 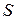поверхности, равна

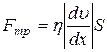. (21)

Если плотность потока массы 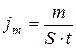, или плотность теплового потока 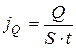, или плотность потока импульса 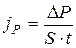является величиной постоянной, то в уравнениях диффузии, теплопроводности и внутреннего трения можно перейти от бесконечно малых изменений величин к конечным разностям и эти уравнения записать в виде

, , .

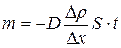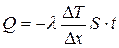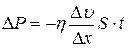Для твердых тел и жидкостей коэффициенты 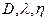определяются экспериментально, для идеальных газов

, , .

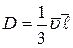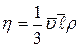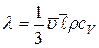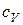- удельная теплоемкость газа при постоянном объеме .

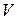ТЕРМОДИНАМИКА.

Внутренняя энергия.

Внутренняя энергия 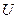вещества складывается из кинетической энергии отдельных молекул и потенциальной энергии их взаимодействия.

Числом степеней свободы молекулы называется число независимых координат, определяющих положение молекулы в пространстве.

Закон Больцмана о равномерном распределении энергии по степеням свободы: на каждую поступательную и вращательную степень свободы молекулы приходится энергия, равная 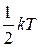, а на каждую колебательную степень свободы – энергия, равная .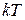