Основы молекулярной физики и термодинамики
Молекулярно – кинетическая теория идеальных газов
· Закон Бойля – Мариотта (изотермический процесс):
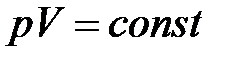 при
при 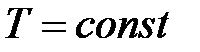 ,
, 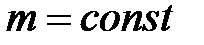 ,
,
где 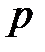 – давление, Па;
– давление, Па; 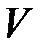 – объем, м3;
– объем, м3; 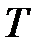 – термодинамическая температура, К;
– термодинамическая температура, К; 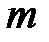 – масса газа, кг.
– масса газа, кг.
· Закон Гей-Люссака (изобарный процесс):
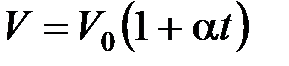 , или
, или 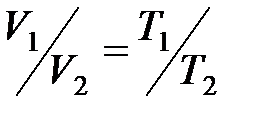 при
при 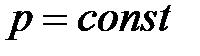 ,
, 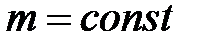 ;
;
· Закон Шарля (изохорный процесс):
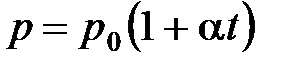 , или
, или 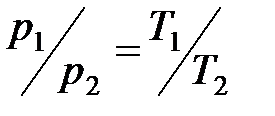 при
при 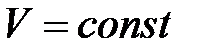 ,
, 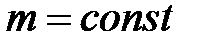 ,
,
где 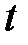 – температура по шкале Цельсия, °C;
– температура по шкале Цельсия, °C; 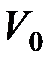 и
и 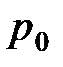 – соответственно объем и давление при
– соответственно объем и давление при 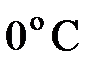 ; коэффициент
; коэффициент 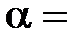 1/273 К-1; индексы 1 и 2 относятся к произвольным состояниям.
1/273 К-1; индексы 1 и 2 относятся к произвольным состояниям.
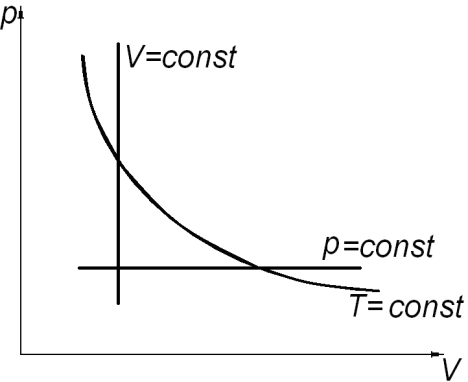
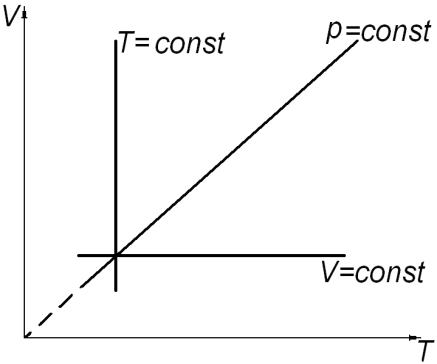
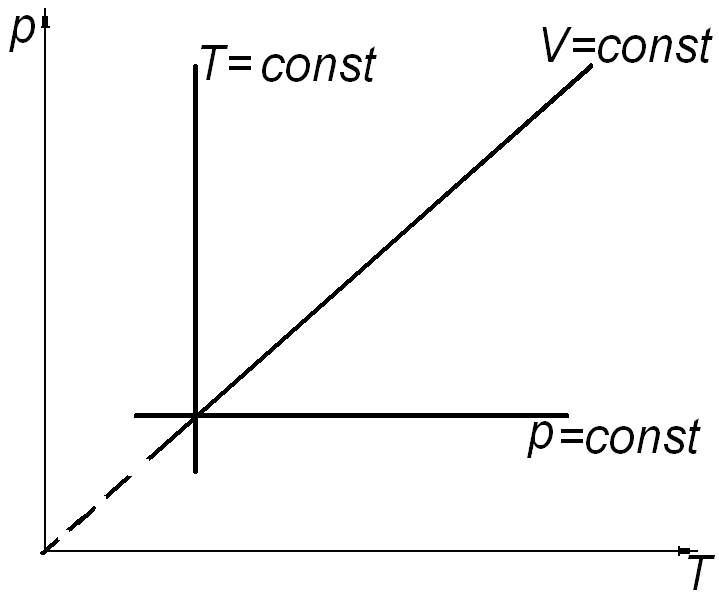
а) б) в)
Рис. 2.
Состояние системы, находящейся в тепловом равновесии, изображают точкой на плоскости в прямоугольной системе координат, на осях которой откладывают в зависимости от условий задачи параметры: p, V (рис. 2. а); V, T (рис. 2. б); p, T (рис. 2. в). Равновесный процесс, в котором участвует газ, изображают в виде графиков между соответствующими параметрами p и V; V и T; p и T. На диаграммах (рис. 2. а, б, в) представлены графики изопроцессов в различных системах координат.
· Закон Дальтона для давления смеси п идеальных газов
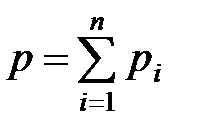 ,
,
где 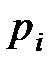 – парциальное давление
– парциальное давление 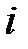 -го компонента смеси.
-го компонента смеси.
· Уравнение состояния идеального газа (уравнение Клапейрона – Менделеева)
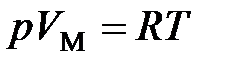 (для 1 моль газа),
(для 1 моль газа),
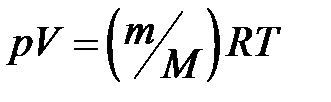 (для произвольной массы газа),
(для произвольной массы газа),
где 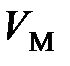 – молярный объем, м3/моль;
– молярный объем, м3/моль; 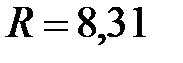 Дж/(моль×К) – молярная универсальная газовая постоянная;
Дж/(моль×К) – молярная универсальная газовая постоянная; 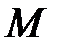 – молярная масса газа, кг/моль;
– молярная масса газа, кг/моль; 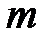 – масса газа, кг;
– масса газа, кг; 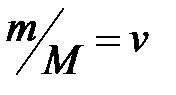 – количество вещества, моль.
– количество вещества, моль.
· Зависимость давления газа от концентрации п молекул и температуры 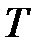
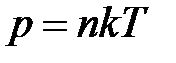 ,
,
где 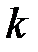 – постоянная Больцмана (
– постоянная Больцмана ( 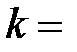 R/Na,
R/Na, 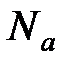 – постоянная Авогадро); n = N/V – концентрация молекул, м-3.
– постоянная Авогадро); n = N/V – концентрация молекул, м-3.
· Основное уравнение молекулярно-кинетической теории идеальных газов
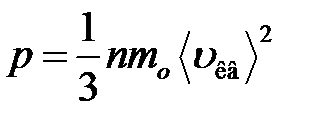 ,
,
или
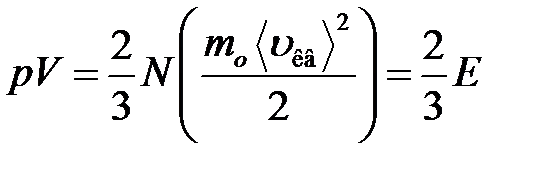 ,
,
или
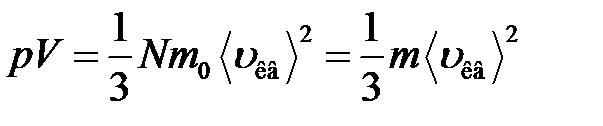 ,
,
где 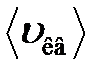 – средняя квадратичная скорость молекул;
– средняя квадратичная скорость молекул; 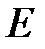 – суммарная кинетическая энергия поступательного движения всех молекул газа; п – концентрация молекул;
– суммарная кинетическая энергия поступательного движения всех молекул газа; п – концентрация молекул; 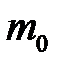 – масса одной молекулы;
– масса одной молекулы; 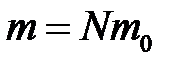 – масса газа; N – число молекул в объеме газа V.
– масса газа; N – число молекул в объеме газа V.
· Скорость молекул:
наиболее вероятная
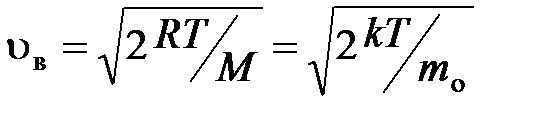 ;
;
средняя квадратичная
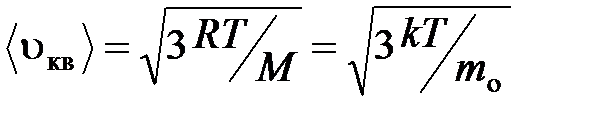 ;
;
средняя арифметическая
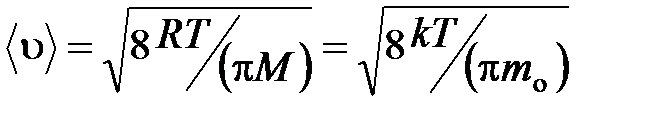 .
.
· Средняя кинетическая энергия поступательного движения молекулы идеального газа
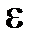 0 = 3kT/2.
0 = 3kT/2.
· Закон Максвелла для распределения молекул идеального газа по скоростям
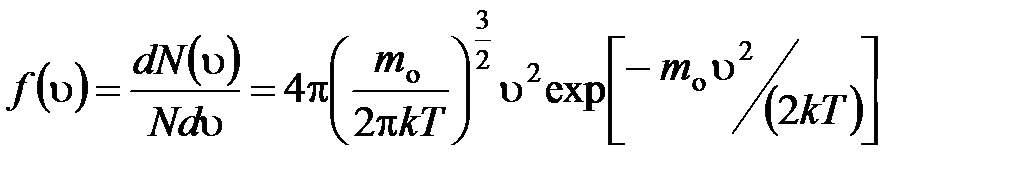 ,
,
где 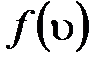 – функция распределения молекул по скоростям, которая определяет относительное число молекул
– функция распределения молекул по скоростям, которая определяет относительное число молекул 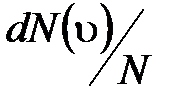 из общего числа N молекул, скорости которых лежат в интервале от
из общего числа N молекул, скорости которых лежат в интервале от 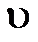 до
до 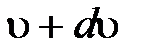 .
.
· Закон Максвелла для распределения молекул идеального газа по энергиям теплового движения
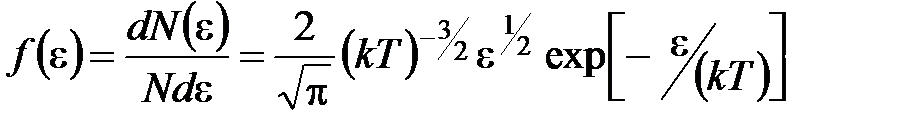 ,
,
где 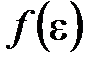 – функция распределения молекул по энергиям теплового движения, которая определяет относительное число молекул
– функция распределения молекул по энергиям теплового движения, которая определяет относительное число молекул 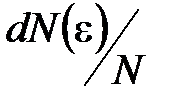 из общего числа N молекул, имеющие кинетические энергии
из общего числа N молекул, имеющие кинетические энергии 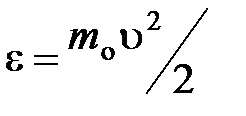 , заключенные в интервале от
, заключенные в интервале от 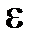 до
до 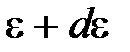 .
.
· Барометрическая формула
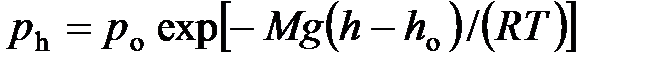 ,
,
где 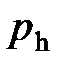 и
и 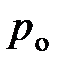 давление газа на высоте
давление газа на высоте 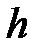 и
и 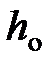 .
.
· Распределение Больцмана во внешнем потенциальном поле
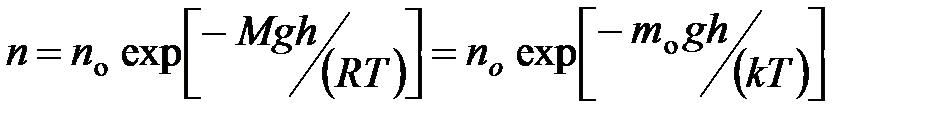 ,
,
где п и 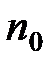 – концентрация молекул на высоте
– концентрация молекул на высоте 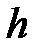 и
и 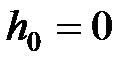 ;
; 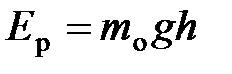 – потенциальная энергия молекулы в поле тяготения.
– потенциальная энергия молекулы в поле тяготения.
· Среднее число соударений, испытываемых молекулой газа за 1 с:
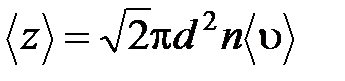 ,
,
где 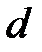 –эффективный диаметр молекулы; п – концентрация молекул;
–эффективный диаметр молекулы; п – концентрация молекул; 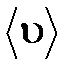 – средняя арифметическая скорость молекул.
– средняя арифметическая скорость молекул.
· Средняя длина свободного пробега молекул газа
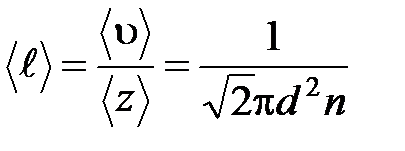 .
.
· Закон теплопроводности Фурье
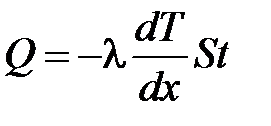 ,
,
где 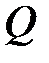 – теплота, прошедшая посредством теплопроводности через площадь
– теплота, прошедшая посредством теплопроводности через площадь 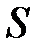 за время
за время 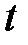 ;
; 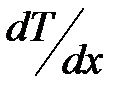 – градиент температуры;
– градиент температуры; 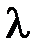 – теплопроводность:
– теплопроводность:
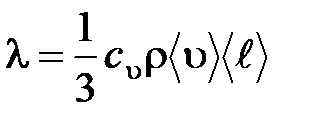 ,
,
где 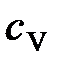 – удельная теплоемкость газа при постоянном объеме; ρ – плотность газа;
– удельная теплоемкость газа при постоянном объеме; ρ – плотность газа; 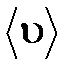 – средняя арифметическая скорость теплового движения его молекул;
– средняя арифметическая скорость теплового движения его молекул; 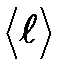 – средняя длина свободного пробега молекул.
– средняя длина свободного пробега молекул.
· Закон диффузии Фика
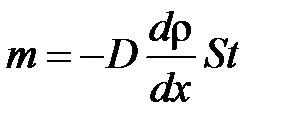 ,
,
где 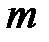 – масса вещества, переносимая посредством диффузии через площадь
– масса вещества, переносимая посредством диффузии через площадь 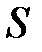 за время
за время 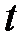 ;
; 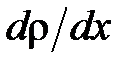 – градиент плотности,
– градиент плотности, 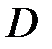 – диффузия:
– диффузия:
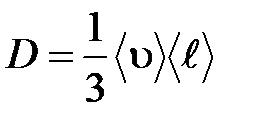 .
.
· Закон Ньютона для внутреннего трения (вязкости)
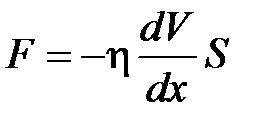 ,
,
где 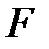 – сила внутреннего трения между движущимися слоями площадью
– сила внутреннего трения между движущимися слоями площадью 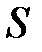 ;
; 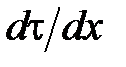 – градиент скорости;
– градиент скорости; 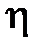 – динамическая вязкость Па×с:
– динамическая вязкость Па×с:
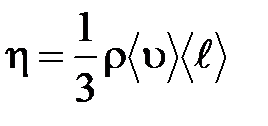 .
.
Основы термодинамики
· Средняя кинетическая энергия поступательного движения, приходящаяся на одну степень свободы молекул,
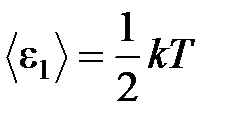 .
.
· Средняя энергия молекулы
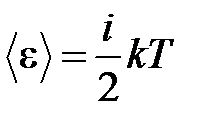 ,
,
где 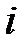 – сумма поступательных, вращательных и удвоенного числа колебательных степеней свободы
– сумма поступательных, вращательных и удвоенного числа колебательных степеней свободы 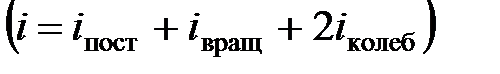 .
.
· Внутренняя энергия идеального газа
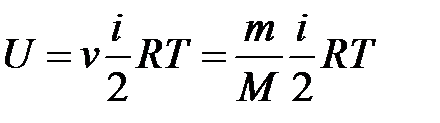 ,
,
где 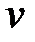 – количество вещества;
– количество вещества; 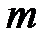 – масса газа;
– масса газа; 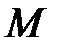 – молярная масса газа;
– молярная масса газа; 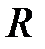 – универсальная газовая постоянная.
– универсальная газовая постоянная.
· Первое начало термодинамики
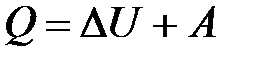 ,
,
где 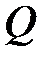 – количество теплоты, сообщенное системе или отданное ею;
– количество теплоты, сообщенное системе или отданное ею; 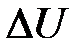 – изменение ее внутренней энергии;
– изменение ее внутренней энергии; 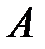 – работа системы против внешних сил.
– работа системы против внешних сил.
· Первое начало термодинамики для малого изменения состояния системы
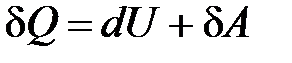 .
.
· Связь между молярной 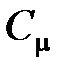 и удельной
и удельной 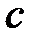 теплоемкостями газа
теплоемкостями газа
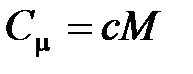 ,
,
где 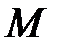 – молярная масса газа.
– молярная масса газа.
· Молярные теплоемкости газа при постоянном объеме и постоянном давлении
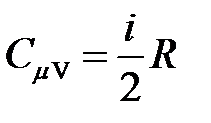 ,
, 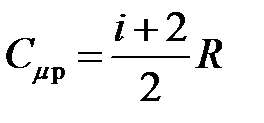 .
.
· Уравнение Майера
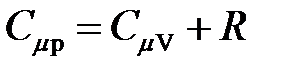 .
.
· Изменение внутренней энергии идеального газа
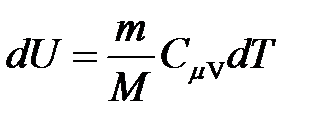 .
.
· Работа, совершаемая газом при изменении его объема:
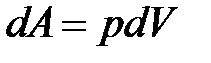 .
.
· Полная работа при изменении объема газа
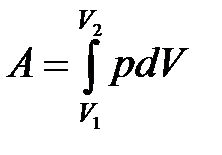 ,
,
где 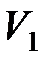 и
и 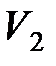 – соответственно начальный и конечный объемы газа.
– соответственно начальный и конечный объемы газа.
· Работа газа:
при изобарном процессе
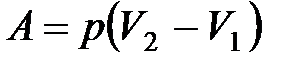 или
или 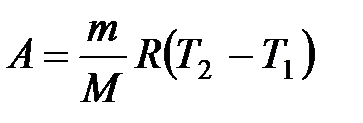 ;
;
при изотермическом процессе
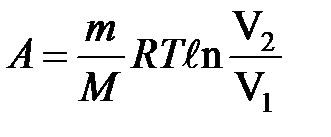 или
или 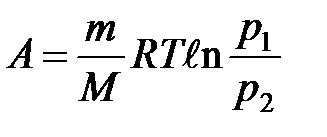 .
.
· Уравнение адиабатного процесса (уравнение Пуассона)
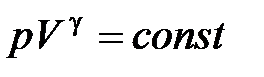 ,
, 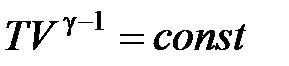 ,
, 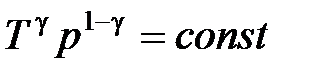 ,
,
где 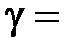 Cp/CV = (i + 2)/i – показатель адиабаты.
Cp/CV = (i + 2)/i – показатель адиабаты.
· Работа в случае адиабатного процесса
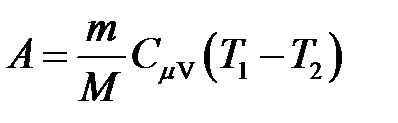 , или
, или
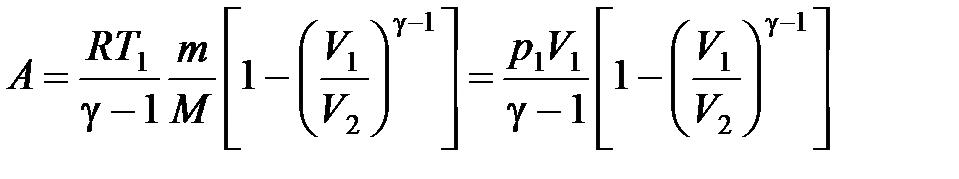 ,
,
где 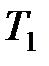 ,
, 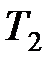 , и
, и 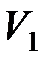 ,
, 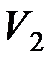 – соответственно начальные и конечные температура и объем газа.
– соответственно начальные и конечные температура и объем газа.
· Термический коэффициент полезного действия для кругового процесса (цикла)
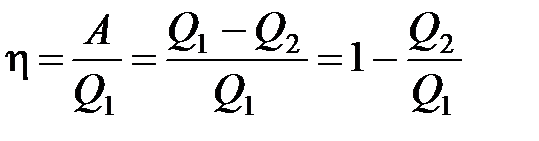 ,
,
где 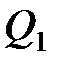 – количество теплоты, полученное системой;
– количество теплоты, полученное системой; 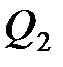 – количество теплоты, отданное системой;
– количество теплоты, отданное системой; 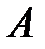 – работа, совершаемая за цикл.
– работа, совершаемая за цикл.
· Термический коэффициент полезного действия цикла Карно
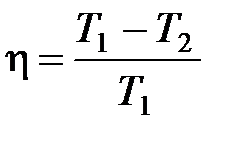 ,
,
где 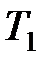 – температура нагревателя;
– температура нагревателя; 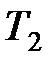 – температура холодильника.
– температура холодильника.
· Изменение энтропии при равновесном переходе из состояния 1 в состояние 2
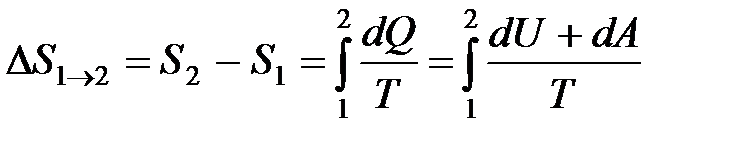 .
.
Статистическое толкование энтропии приводит к расчетной зависимости
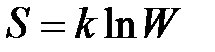 ,
,
где 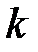 – постоянная Больцмана,
– постоянная Больцмана, 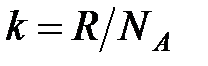 ;
; 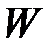 – термодинамическая вероятность.
– термодинамическая вероятность.
Для одного моля идеального газа
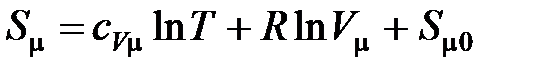 ,
,
где 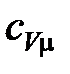 – изохорная молярная теплоемкость газа,
– изохорная молярная теплоемкость газа, 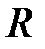 – универсальная газовая постоянная,
– универсальная газовая постоянная, 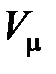 – молярный объем,
– молярный объем, 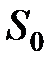 – энтропия одного моля, принятая за начало отсчета.
– энтропия одного моля, принятая за начало отсчета.
