Сечения столкновения частиц
Представленная выше теория оперировала с одной, пока еще не вполне определенной величиной — сечением столкновения частиц σ. Ввиду простоты и физической наглядности этой теории — обстоятельств, которые делают ее столь удобной при качественном анализе процессов, — подобное упущение можно оправдать; однако, если теория претендует на то, чтобы дать количественное описание явлений, необходимо более подробно остановиться на характерных особенностях сечения столкновения частиц σ. Ниже будут рассмотрены некоторые приближенные методы получения оценочных значений величины сечения σ и его зависимости от энергии сталкивающихся частиц.
В дальнейшем будет показано, что σ представляет собой вполне определенную величину, но для этого потребуется либо знание процессов обмена энергией и импульсом при столкновении партнеров, либо умение точно решать кинетическое уравнение Больцмана. Оказывается, что под величиной σ следует понимать диффузионное сечение рассеяния, или, как его еще называют, сечение передачи импульса частиц,которое определяется выражением
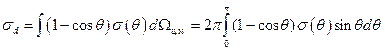 ,
,
здесь θ — угол рассеяния в системе центра масс частиц,
σ(θ) — дифференциальное сечение рассеяния.
Написанное в таком виде сечение ограничено только случаем упругих столкновений частиц. Очень часто процессы соударения частиц достаточно хорошо описываются законами классической механики; при этом уравнение можно переписать в виде
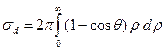 ,
,
где ρ — прицельное расстояние, а угол θ дается соотношением
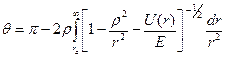 .
.
В последнем уравнении ra определяет расстояние наименьшего сближения частиц (наиболее удаленный от начала координат корень подынтегрального выражения), U(r)— потенциальная энергия взаимодействия иона с нейтральной молекулой, 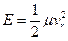 — исходная кинетическая энергия относительного движения сталкивающихся частиц. (Не следует путать кинетическую энергию Е с также обозначенной напряженностью электрического поля.) Хотя законов классической механики явно недостаточно, чтобы определить поведение сечения столкновения σ(θ) при малых углах рассеяния, приведенные выше выражения все же широко используют, поскольку наличие весового множителя (1 - cosθ) при дифференциальном сечении рассеяния в уравнении снижает вклад в диффузионное сечение от рассеяния на малые углы.
— исходная кинетическая энергия относительного движения сталкивающихся частиц. (Не следует путать кинетическую энергию Е с также обозначенной напряженностью электрического поля.) Хотя законов классической механики явно недостаточно, чтобы определить поведение сечения столкновения σ(θ) при малых углах рассеяния, приведенные выше выражения все же широко используют, поскольку наличие весового множителя (1 - cosθ) при дифференциальном сечении рассеяния в уравнении снижает вклад в диффузионное сечение от рассеяния на малые углы.
Строгое вычисление сечения σd требует проведения громоздкого численного интегрирования практически для любого простого по виду потенциала взаимодействия U(r). Часто, однако, достаточно точную оценку величины сечения можно получить из наглядных физических соображений, так что в данном параграфе нам достаточно ограничиться именно этим подходом. Один точный результат можно получить непосредственно из соображений размерности величин, определяющих процесс рассеяния; по-видимому, впервые это сделал лорд Рэлей, который для потенциалавида
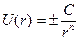
(где С и п — положительные константы) определил зависимость любого сечения столкновения от энергии по соотношению
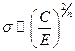 .
.
Понятно, что множитель пропорциональности остается при этом неизвестным. Чтобы простым образом проверить указанный результат, заметим, что, согласно , угол θ является функцией только одного безразмерного параметра 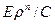 , так что из-за пропорциональности любого сечения соударения σ величине ρdρ приходим к уравнению .
, так что из-за пропорциональности любого сечения соударения σ величине ρdρ приходим к уравнению .
В том случае, когда доминирующую роль в рассеянии частиц играет потенциал притяжения вида С/rn, можно оценить величину σ исходя из простых соображений, выдвинутых Ванье. Дело в том, что при заданной энергии столкновения существует такое прицельное расстояние ρ0, при котором частицы переходят на траекторию постепенного сближения, т. е. Частицы закручиваются. При ρ <ρ0 сталкивающиеся частицы преодолевают потенциальный барьер и сближаются до тех пор, пока не достигнут столь малых расстояний, где доминирует отталкивательное взаимодействие, приводящее в итоге к их разлету. В этих условиях диффузионное сечение рассеяния полагают равным сечению закручивания частиц, или, как говорят, сечению захвата, определяемому уравнением
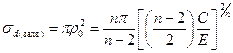 .
.
Особенность заключается в том, что сечение σd оказывается пропорциональным квадрату некоторого характеристического расстояния, зависящего от энергии сталкивающихся частиц. Это наводит на мысль, что если мы дадим более общее определение характеристическому расстоянию, связав его с эффективным диаметром столкновения, то полученные результаты сможем распространить на потенциалы произвольного вида, соответствующие как притяжению, так и отталкиванию.
Наиболее простой выбор характеристического расстояния следует из равенства потенциальной энергии взаимодействия частиц их начальной кинетической энергии относительного движения (т.е. эквивалентен выбору расстояния наименьшего сближения при лобовом ударе). В результате находим
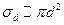 ,
,
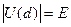 .
.
Даже для потенциалов сложного вида можно получить вполне приемлемые оценки сечения рассеяния частиц и зависимости его от энергии столкновения. Даже в том случае, когда из-за сложности потенциала мы не имеем возможности разрешить уравнение в явном виде относительно d, результаты все же можно представить в форме параметрической зависимости. Для этого выбирают произвольное значение d, по уравнению находят σd и по уравнению — соответствующее значение энергии столкновения Е.
