Теория Кирквуда для полярных жидкостей
Недостатки теории Онзагера отчасти преодолеваются в теории Кирквуда.
Кирквуд рассматривает шаровой образец А из полярного диэлектрика (Рис. 6‑11). Одна из дипольных молекул, например i-я, с моментом 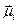 индуцирует в шаре А дипольный момент
индуцирует в шаре А дипольный момент 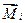
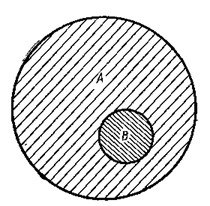 Рис. 6‑11. Сферическая область В, мысленно выделенная в шаровом диэлектрике А для расчета диэлектрической проницаемости. Рис. 6‑11. Сферическая область В, мысленно выделенная в шаровом диэлектрике А для расчета диэлектрической проницаемости. |
Для вычисления 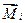 , внутри шара А мысленно выделим сферический объем В радиуса r0 сцентром в точке, где находится i-ямолекула. Радиус выбирается достаточно большим по сравнению с размерами молекулы, чтобы за пределами области В среду можно было считать непрерывной и обладающей макроскопической диэлектрической проницаемостью ε. Если известно, что i-я молекула в шаре В создает момент
, внутри шара А мысленно выделим сферический объем В радиуса r0 сцентром в точке, где находится i-ямолекула. Радиус выбирается достаточно большим по сравнению с размерами молекулы, чтобы за пределами области В среду можно было считать непрерывной и обладающей макроскопической диэлектрической проницаемостью ε. Если известно, что i-я молекула в шаре В создает момент 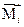 , то момент
, то момент 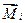 может быть выражен через
может быть выражен через 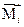 .
.
Определяя 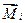 через величину
через величину 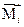 , путем решения электростатической задачи и считая для простоты, что радиусы шаров А и В стремятся к бесконечности так, что
, путем решения электростатической задачи и считая для простоты, что радиусы шаров А и В стремятся к бесконечности так, что 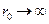 и
и 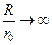 (где R — радиус шара A), Кирквуд нашел
(где R — радиус шара A), Кирквуд нашел
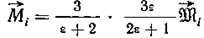 .
.
При таком способе решения фактически рассматривается бесконечный диэлектрик. Отличие теории Кирквуда от теории Онзагера состоит в том, что отдельная молекула с моментом 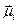 заменяется сферической областью с моментом
заменяется сферической областью с моментом 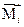 . Тем самым устраняются недостатки теории Онзагера, предполагающей, что форма молекулы сферическая и диэлектрик вблизи молекулы непрерывный.
. Тем самым устраняются недостатки теории Онзагера, предполагающей, что форма молекулы сферическая и диэлектрик вблизи молекулы непрерывный.
Теория Кирквуда дает следующее выражение для диэлектрической проницаемости полярной жидкости:
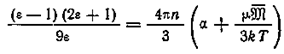 ,
,
где 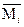 - средняя величина электрического момента области B в направлении дипольного момента молекулы, находящейся в центре области,
- средняя величина электрического момента области B в направлении дипольного момента молекулы, находящейся в центре области,
которое можно было бы использовать для вычисления ε, если бы были известны дипольный момент молекулы μ и средняя величина 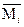 момента достаточно большой сферической области В.
момента достаточно большой сферической области В.
Вычисление момента большой области В представляет собой сложную самостоятельную задачу, которая в рамках теории Кирквуда не решается. Выражением можно пользоваться для приближенной оценки ε, если считать, что область В имеет небольшие размеры и содержит только рассматриваемую молекулу и z ее ближайших соседей. Любая молекула находится в поле соседних молекул, поэтому ее ориентация зависит от ориентации соседних молекул. Энергия взаимодействия двух соседних молекул w зависит от угла g, образованного направлениями диполей этих молекул. Средняя величина момента области В, содержащей молекулу и z ее ближайших молекул, в направлении момента молекулы равна
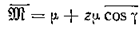 ,
,
где 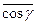 — среднее значение
— среднее значение 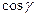 . Очевидно, что
. Очевидно, что
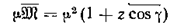 ;
;
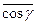 можно вычислить, учитывая зависимость энергии взаимодействия двух соседних молекул w от угла, образованного направлениями их дипольных моментов:
можно вычислить, учитывая зависимость энергии взаимодействия двух соседних молекул w от угла, образованного направлениями их дипольных моментов:
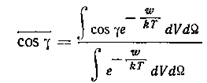 ,
,
где 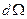 и dV— элементы телесного угла и объема.
и dV— элементы телесного угла и объема.
Вводя обозначение 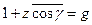 , где g — структурный фактор, уравнение для ε можно записать в виде
, где g — структурный фактор, уравнение для ε можно записать в виде
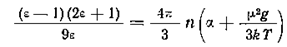 .
.
Кирквуд вычислил структурный фактор для воды и определил значения 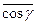 = 0,41 и g = 2,64, так как координационное число z для молекул воды равно 4. При g = 2,64 из уравнения получается величина ε = 67, которая ближе к экспериментальному значению ε = 81, чем диэлектрическая проницаемость воды, вычисленная на основе теории Онзагера. Как известно, теория Онзагера дает значение ε = 31. Расхождение теории Кирквуда с опытом отчасти обусловлено тем, что в качестве области В выбран ограниченный объем, в котором содержатся молекула и z ее ближайших соседей, т. е. всего пять молекул.
= 0,41 и g = 2,64, так как координационное число z для молекул воды равно 4. При g = 2,64 из уравнения получается величина ε = 67, которая ближе к экспериментальному значению ε = 81, чем диэлектрическая проницаемость воды, вычисленная на основе теории Онзагера. Как известно, теория Онзагера дает значение ε = 31. Расхождение теории Кирквуда с опытом отчасти обусловлено тем, что в качестве области В выбран ограниченный объем, в котором содержатся молекула и z ее ближайших соседей, т. е. всего пять молекул.
Для большинства жидкостей структурные факторы не известны, так что для таких жидкостей теория Кирквуда не позволяет вычислять величину диэлектрической проницаемости. Уравнение может быть использовано для определения g по измеренным значениям ε, α и μ.
Основываясь на теории Кирквуда, невозможно точно рассчитать величину диэлектрической проницаемости. В случае очень большой области В неточности в теории Кирквуда связаны с недостаточно строгим учетом упругой поляризации, а именно, с отождествлением поля F, действующего на молекулу, с полем полости Онзагера G. В случае малой области В появляются дополнительные погрешности вследствие учета взаимодействия области В и части шара А за пределами области В с помощью макроскопической диэлектрической проницаемости.
7 Поляризация диэлектриков в переменном поле и диэлектрические потери iv [vi] [vii] [viii]
