Вращательное движение. Моменты инерции, силы, импульса
Примеры решения задач
7. Сила с компонентами (2, -1, 4), H приложена к точке с координатами (–3, 2, 1), м. Найти:
а) момент силы  относительно начала системы координат;
относительно начала системы координат;
б) модуль момента силы M;
в) проекцию Mz момента силы  на ось z.
на ось z.
Дано:  , Н , Н  ,м ,м | Решение По определению момент силы относительно начала системы координат – векторное произведение радиус-вектора 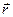 и силы и силы 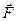 . . |
а)  б) б)  в) в)  | Следотельно,    = [ = [  ] = ] =    = (yFz-zFy) = (yFz-zFy)  +(zFx-xFz) +(zFx-xFz)  + x y z + x y z    +(xFy – yFx) +(xFy – yFx)  = 10 = 10  +14 +14  – 1,0 – 1,0  , Н∙м, (1) , Н∙м, (1) |
z – компонента вектора  и есть проекция Mz момента силы на ось z.
и есть проекция Mz момента силы на ось z.
Следовательно, Mz = -1, Н×м. Модуль момента силы получится из выражения вышеприведенного:  =
=  , Н∙м.
, Н∙м.
Ответ:  , Н×м; M = 17,2 Н×м; Mz = –1 Н×м.
, Н×м; M = 17,2 Н×м; Mz = –1 Н×м.
8. Во сколько раз уменьшится момент инерции однородного сплошного диска оносительно оси, проходящей через его центр инерции (точка О) и перпендикулярной к плоскости диска, если сделать круглый дисковый вырез, как показано на рисунке.
 |
Момент инерции – величина аддитивная. Поэтому момент инерции I3 диска с вырезом относительно точки О равен разности момента инерции диска  относительно точки О и момента инерции малого диска
относительно точки О и момента инерции малого диска  , соответствующего вырезанной части, также относительно точки О, т. е.
, соответствующего вырезанной части, также относительно точки О, т. е.  . В задаче необходимо найти отношение
. В задаче необходимо найти отношение 
 . Обозначим массу диска через m, а радиус диска через R. Тогда масса вырезанной части
. Обозначим массу диска через m, а радиус диска через R. Тогда масса вырезанной части  , а радиус
, а радиус  . Как известно, момент инерции диска
. Как известно, момент инерции диска  относительно оси симметрии равен:
относительно оси симметрии равен:  . Для вычисления момента инерции
. Для вычисления момента инерции  используем теорему Штейнера:
используем теорему Штейнера:
 ,
,
где  – момент инерции малого диска, соответствующего вырезанной части, относительно оси симметрии этого диска, походящей через точку О′. Окончательно
– момент инерции малого диска, соответствующего вырезанной части, относительно оси симметрии этого диска, походящей через точку О′. Окончательно  . Таким образом, искомое отношение
. Таким образом, искомое отношение  = 1,23
= 1,23  .
.
Ответ: момент инерции диска после сделанного выреза уменьшается в 1,2 раза.
9. Тонкий однородный обруч массой m = 2,0 кг и радиусом R = 1,0 м вращается вокруг оси симметрии, перпендикулярной к плоскости обруча, делая n0 = 120 об/мин. Под действием постоянной касательной к поверхности обруча силы Fт = 4,0 Н обруч тормозится и останавливается. Определить время торможения tт и число оборотов Nт, которое сделает обруч от начала торможения до остановки.
| Дано: m = 2,0 кг R = 1,0 м n0 = 120 об/мин = 2 об/с Fт = 4,0 Н | Решение Для вращающегося обруча, на который действует тормозящий момент сил  , уравнение вращательного движения имеет вид , уравнение вращательного движения имеет вид  (1) где I – момент инерции обруча, ε – угловое ускорение. Момент инерции тонкого однородного обруча I = mR². Угловое ускорение постоянно, так как тормозящий момент сил не изменяется. Следотельно, угловая скорость ωсвязана с угловым ускорением формулой (1) где I – момент инерции обруча, ε – угловое ускорение. Момент инерции тонкого однородного обруча I = mR². Угловое ускорение постоянно, так как тормозящий момент сил не изменяется. Следотельно, угловая скорость ωсвязана с угловым ускорением формулой |
| а) tт –? б) Nт –? |
 (2)
(2)
где ω0 – начальная угловая скорость обруча. Знак «минус» в выражении (2) показывает, что вращение равнозамедленное. Число оборотов N связано с углом поворота обруча φ  соотношением
соотношением
 . (3)
. (3)
В конце времени торможения угловая скорость обруча равна нулю, и из формул (1) и (2) получим
 с
с  с.
с.
Для числа оборотов Nт за время торможения из выражения (3) следует:

 об.
об.
Ответ: tт = 6,3 с; Nт = 13 об.
10. Небольшое тело массой m = 200 г брошено по углом α= 60° к горизонту со скоростью 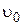 = 10 м/с. Выразить зависимость момента импульса тела
= 10 м/с. Выразить зависимость момента импульса тела  от времени в системе координат, изображенной на рисунке, относительно точки О.
от времени в системе координат, изображенной на рисунке, относительно точки О.
Определить модуль изменения момента импульса  для положения тела в точке наивысшего подъема О΄ и точке падения на землю А.
для положения тела в точке наивысшего подъема О΄ и точке падения на землю А.


Дано: m = 200г α= 60°  = 10 м/с = 10 м/с | Решение Введем правовинтовую систему координат OXYZ, как показано на рисунке. Поскольку при движении тела на него действует только сила тяжести, то из уравнения моментов  можно определить момент импульса можно определить момент импульса  |
а) L(t) –? б)  –? –? |
где  , в котором mg – сила тяжести, l – плечо силы относительно точки О. Знак (-) обусловлен тем, что момент силы
, в котором mg – сила тяжести, l – плечо силы относительно точки О. Знак (-) обусловлен тем, что момент силы  в соответствии с правилом правого винта направлен в сторону противоположную оси z.
в соответствии с правилом правого винта направлен в сторону противоположную оси z.
Плечо l найдем как l =  , так как вдоль оси x силы не действуют и движение равномерное. Тогда момент импульса
, так как вдоль оси x силы не действуют и движение равномерное. Тогда момент импульса
 . (1)
. (1)
Время достижения телом точки наивысшего подъема  определяется выражением
определяется выражением  с (так как
с (так как  ).
).
Время достижения телом точки А в два раза больше времени  (как известно, время подъема равно времени спуска тела).
(как известно, время подъема равно времени спуска тела).
Окончательно производя необходимые вычисления, получим для  (кг×м2)/с; для модуля изменения момента импульса из (*), учитывая, что в начальный момент времени
(кг×м2)/с; для модуля изменения момента импульса из (*), учитывая, что в начальный момент времени 

 (кг∙м²)/с.
(кг∙м²)/с.
Ответ:  (кг∙м²)/с;
(кг∙м²)/с;  (кг∙м²)/с.
(кг∙м²)/с.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1.24. Сфера радиусом R = 2,0 м равномерно вращается вокруг вертикальной оси симметрии, делая 30 об/мин. Внутри сферы находится шарик. Найти высоту h, соответствующую положению равновесия шарика. При какой наименьшей угловой скорости радиус вращения шарика будет 0,9 R? Шарик считать материальной точкой.
(h = 1,0 м;ω = 3,4 рад/с)
1.25. Тело участвует в двух вращательных движениях, происходящих со скоростями  и
и  (a = 1,0 рад/с3). Определить:
(a = 1,0 рад/с3). Определить:
а) на какой угол j повернется тело за первые 3,0 с;
б) какой угол составляет ось вращения, вокруг которой происходит поворот, с осью Х.
(а) j = 20 рад, б) a = 63°)
1.26. Тело вращается вокруг неподвижной оси так, что угол его поворота меняется в зависимости от времени t по закону  , где а>0; b>0. Найти момент времени t, в который тело остановится, а также число оборотов N тела до остановки.
, где а>0; b>0. Найти момент времени t, в который тело остановится, а также число оборотов N тела до остановки.
(  ;
;  )
)
1.27. Материальная точка движется по окружности радиусом R со скоростью u = kt, где k>0. Найдите зависимость от времени модуля полного ускорения точки; постройте графики зависимости тангенциального и нормального ускорений от времени.
(  )
)
1.28. Определить полное ускорение W в момент времени t = 3,0 c точки, находящейся на ободе колеса радиусом R = 0,50 м, вращающегося согласно уравнению j = Аt+Вt3, где А = 2,0 рад/с; В = 0,20 рад/c3. Изобразите графики нормального и полного ускорений Wn = f(t) и W = f(t) на интервале 0<t<3 с.
(W = 27 м/с2)
1.29. Точка движется по окружности с постоянным тангенциальным ускорением. Через некоторый промежуток времени t после начала движения, угол между полным ускорением и радиусом окружности равен 45°. Чему равно угловое ускорение точки?
(e  )
)
1.30. Материальная точка (частица) массой m брошена под углом a к горизонту с начальной скоростью 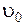 . Траектория полета частицы лежит в плоскости Х, Y. Ось Z направлена "на нас".
. Траектория полета частицы лежит в плоскости Х, Y. Ось Z направлена "на нас".
 |

Найти зависимость от времени:
а) момента силы 
 , действующего на частицу;
, действующего на частицу;
б) момента импульса частицы  относительно начала координат.
относительно начала координат.
(а)  ; б)
; б)  ) .
) .
1.31. Две материальные точки массами m1 и m2 соединены жестким невесомым стрежнем длиной L. Найти положение центра масс системы Хс и момент инерции I этой системы относительно перпендикулярной к стержню оси, проходящей через центр масс.
(  ;
;  )
)
1.32. Тело массой m = 0,10 кг брошено с некоторой высоты в горизонтальном направлении со скоростью u0 = 20 м/с. Найти модуль приращения момента импульса тела  относительно точки бросания за первые t = 5 с.
относительно точки бросания за первые t = 5 с.
(  = 2,5 ∙102 кгм2/с)
= 2,5 ∙102 кгм2/с)
1.33. Сила с компонентами (3, 4, 5) Н приложена к точке с координатами (4, 2, 3) (м). Найти:
а) момент силы  относительно начала координат;
относительно начала координат;
б) модуль вектора  ;
;
в) проекцию на ось Z момента силы Мz.
(  (Н×м),
(Н×м),  = 15 Н×м)
= 15 Н×м)
1.34. Найти момент инерции однородной прямоугольной пластинки массой m, длиной а и шириной b относительно перпендикулярной к ней оси, проходящей через одну из вершин пластинки.
(  )
)
1.35. Цилиндр, расположенный горизонтально, может вращаться вокруг оси, совпадающей с осью цилиндра. Масса цилиндра m1 = 12 кг. На цилиндр намотан шнур, к которому привязали гирю массой m2 = 1,0 кг. С каким ускорением будет опускаться гиря? Какова сила натяжения шнура во время движения гири?
(W = 1,4 м/с2; T = 8,4 Н)
1.36. На обод маховика диаметром D = 60 cм намотан шнур, к концу которого привязан груз массой m = 2,0 кг. Определить момент инерции маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t = 3,0 с приобрел угловую скорость w = 9,0 рад/с.
(J = 1,8 кг×м2)
1.37. Тонкий обруч радиусом R раскрутили вокруг его оси до угловой скорости  и положили (опустили) на горизонтальный стол. Через какое время t обруч остановится, если коэффициент трения между столом и обручем равен m? Сколько оборотов N сделает обруч до полной остановки?
и положили (опустили) на горизонтальный стол. Через какое время t обруч остановится, если коэффициент трения между столом и обручем равен m? Сколько оборотов N сделает обруч до полной остановки?
(  ;
;  )
)
1.38. С какой угловой скоростью должен вращаться сосуд в виде усеченного конуса, чтобы шарик, лежащий на его дне, выкатился из него? Диаметр верхнего основания равен d. Стенки сосуда наклонены к горизонту под углом a.
(  )
)
1.39. Из сплошного однородного цилиндра радиусом R сделали полый, удалив внутреннюю часть радиусом R/2 от оси симметрии. Во сколько раз изменится момент инерции тела относительно указанной оси?
(  )
)
1.40. Из сплошного однородного цилиндра сделали полый, удалив половину его массы. Как изменится момент инерции J цилиндра относительно его оси и во сколько раз? Как и во сколько раз изменится момент импульса указанных цилиндров, если они вращаются с одинаковой угловой скоростью?
(  )
)
1.41. В сплошном однородном диске радиусом R просверлили сквозное отверстие радиусом R/2 от оси симметрии. Как изменится момент инерции тела относительно указанной оси по отношению к первоначальному?
(  )
)
1.42. Два однородных цилиндра с одинаковыми высотами h и равными массами m вращаются относительно своих осей симметрии. Соотношение плотностей материалов цилиндров r1 = (3/4)r2. Сравнить вращающие моменты сил, если угловые ускорения цилиндров одинаковы, а моменты сил трения Мтр равны.
(  )
)
1.43. Грузик массой 5,0 г, привязанный к нити длиной l = 50 см, вращается вокруг вертикальной оси и описывает окружность в горизонтальной плоскости. Какой угол j образует нить с вертикалью, если частота вращения n = 1,0 c-1. Чему равен модуль проекции момента импульса на ось вращения?
(j = 60°; L  = 5,9∙10-2 (кг∙м²)/с)
= 5,9∙10-2 (кг∙м²)/с)
