Закон сохранения энергии
Закон сохранения энергии - результат обобщения многих экспериментальных данных. Идея этого закона принадлежит М.В.Ломоносову, изложившему закон сохранения материи и движения, а количественная формулировка закона сохранения энергии дана немецким врачом Ю. Майером и немецким естествоиспытателем Г. Гельмгольцем
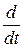 (m1
(m1 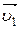 +m2
+m2 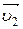 +…+mn
+…+mn 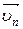 ) =
) = 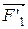 +
+ 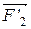 +… +
+… + 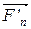 +
+ 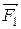 +
+ 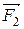 +…+
+…+ 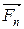 .
.
Рассмотрим систему материальных точек массами m1, m2,..., mn, движущихся со скоростями 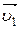 ,
, 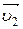 , ...,
, ..., 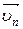 . Пусть
. Пусть 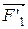 ,
, 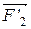 , ...,
, ..., 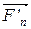 - равнодействующие внутренних консервативных сил, действующих на каждую из этих точек, a
- равнодействующие внутренних консервативных сил, действующих на каждую из этих точек, a 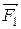 ,
, 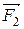 , ...,
, ..., 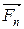 - равнодействующие внешних сил, которые также будем считать консервативными. Кроме того, будем считать, что на материальные точки действуют еще и внешние неконсервативные силы; равнодействующие этих сил, действующих на каждую из материальных точек, обозначим
- равнодействующие внешних сил, которые также будем считать консервативными. Кроме того, будем считать, что на материальные точки действуют еще и внешние неконсервативные силы; равнодействующие этих сил, действующих на каждую из материальных точек, обозначим 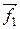 ,
, 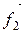 , ...,
, ..., 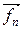 . При u<<c массы материальных точек постоянны и уравнения второго закона Ньютона для этих точек следующие:
. При u<<c массы материальных точек постоянны и уравнения второго закона Ньютона для этих точек следующие:
m1 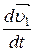 =
= 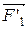 +
+ 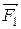 +
+ 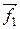 ,
,
m1 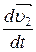 =
= 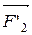 +
+ 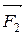 +
+ 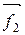 ,
,
mn 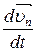 =
= 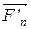 +
+ 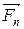 +
+ 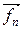 .
.
Двигаясь под действием сил, точки системы за интервал времени dt совершают перемещения, соответственно равные 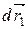 ,
,  , ...,
, ..., 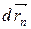 . Умножим каждое из уравнений скалярно на соответствующее перемещение и, учитывая, что
. Умножим каждое из уравнений скалярно на соответствующее перемещение и, учитывая, что 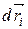 =
=  dt, получим:
dt, получим:
m1 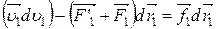 ,
,
m2 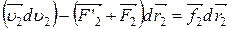 ,
,
mn 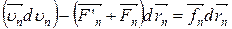 .
.
Сложив эти уравнения, получим
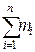
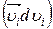 -
- 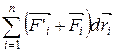 =
= 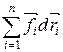 (3.14)
(3.14)
Первый член левой части равенства (3.14)
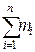
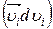 =
= 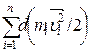 = dWк ,
= dWк ,
где dWк есть приращение кинетической энергии системы. Второй член 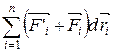 равен элементарной работе внутренних и внешних консервативных сил, взятой со знаком минус, т. е. равен элементарному приращению потенциальной энергии dWp системы (см. (3.6).
равен элементарной работе внутренних и внешних консервативных сил, взятой со знаком минус, т. е. равен элементарному приращению потенциальной энергии dWp системы (см. (3.6).
Правая часть равенства (3.11) задает работу внешних неконсервативных сил, действующих на систему. Таким образом, имеем
d(Wк + Wp) = δА. (3.15)
При переходе системы из состояния 1 в какое-либо состояние 2
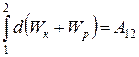 ,
,
т. е. изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативными силами. Если внешние неконсервативные силы отсутствуют, то из (3.15) следует, что
d(Wк + Wp) = 0 ,
откуда
Wк + Wp = W = const , (3.16)
т. е. полная механическая энергия системы сохраняется постоянной. Выражение (3.16) представляет собой закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем.
Механические системы, на тела которых действуют только консервативные силы (внутренние и внешние), называются консервативными системами. Закон сохранения механической энергии можно сформулировать так: в консервативных системах полная механическая энергия сохраняется.
Закон сохранения механической энергии связан с однородностью времени, т. е. инвариантностью физических законов относительно выбора начала отсчета времени. Например, при свободном падении тела в поле сил тяжести его скорость и пройденный путь зависят лишь от начальной скорости и продолжительности свободного падения тела и не зависят от того, когда тело начало падать.
Существует еще один вид систем - диссипативные системы, в которых механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. Этот процесс получил название диссипации (или рассеяния) энергии. Строго говоря, все системы в природе являются диссипативными.
В консервативных системах полная механическая энергия остается постоянной. Могут происходить лишь превращения кинетической энергии в потенциальную и обратно в эквивалентных количествах, так что полная энергия остается неизменной. Поэтому этот закон не есть просто закон количественного сохранения энергии, а закон сохранения и превращения энергии, выражающий и качественную сторону взаимного превращения различных форм движения друг в друга. Закон сохранения и превращения энергии - фундаментальный закон природы, он справедлив как для систем макроскопических тел, так и для систем микротел.
В системе, в которой действуют также неконсервативные силы, например силы трения, полная механическая энергия системы не сохраняется. Следовательно, в этих случаях закон сохранения механической энергии несправедлив. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом и заключается физическая сущность закона сохранения и превращения энергии - сущность неуничтожимости материи и ее движения.
