Порядок выполнения работы. 1. Опорную призму укрепить на конце стержня

1. Опорную призму укрепить на конце стержня. Поместить маятник ребром опорной призмы на подставку и привести в колебательное движение так, чтобы амплитуда колебаний не превышала ~ 6⁰. Это означает, что наибольшее отклонение нижнего конца стержня от положения равновесия не должно превышать 0,1 расстояния от конца до опорной призмы.

2. Определить секундомером время t десяти полных колебаний. Значения х и t записать в табл. 1.

Таблица 1

Номер опыта i	Расстояние x, м	Число колебаний n	Время t, с	Период колебаний T, с
…

3. Перемещать опорную призму к середине стержня через 0,01 м измеряя для каждого ее положения время 10 полных колебаний и занося результаты измерения в табл. 1.

Измерения можно прекратить после того, как получится, что время 10 колебаний стало больше времени, полученного при самом первом измерении, когда опорная призма находилась на конце стержня.

Перевертывать маятник и определять периоды для различных положений призмы на другом конце стержня нет необходимости.

4. Вычислить периоды колебаний Т по формуле Т = t/n и занести в табл.

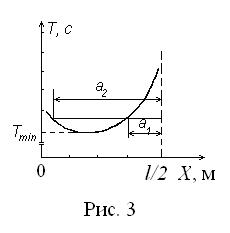5. Построить график T = f(x). Для этого по оси абсцисс откладывают расстояние х от конца стержня до опорной призмы, а по оси ординат - соответствующее значение периода.

Масштаб по оси ординат следует выбрать по возможности больше, чтобы точнее определить по графику величины L и T . Для этого за начало отсчета по оси ординат нужно взять не нуль, а некоторое значение периода, меньшее Т_min, но близкое к нему.

Отметить на оси абсцисс середину стержня и провести через эту точку прямую, параллельную оси ординат. В итоге получится график, показанный на рис. 3.

6. По графику определить для 5 различных значения периода соответствующие им значений приведенной длины маятника L (5). Для этого нужно провести 5 прямых, параллельных оси абсцисс так, чтобы каждая прямая пересекала построенную кривую в двух точках. Значения Т и L, определенные для каждой такой прямой, записать в табл. 2.

Таблица 2

Номер опыта i	Период колебаний T, с	Приведенная длина L, м	Ускорениеgi, м/с2	(gi - <g>)
t(α, n)			<g>	∑(gi - <g>)

7. По формуле (6) вычислить g для каждого измерения и найти среднее значение <g>

.

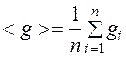8. Вычислить относительную погрешность по формуле

.

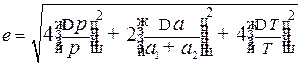Здесь Δa = Δa₁ = Δa₂. Для нахождения ΔT необходимо произвести

измерения T 5 раз для одного из значений x и вычислить абсолютную погрешность по формуле

,

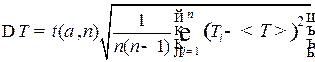где t(α, n) - коэффициент Стьюдента.

9. Вычислить абсолютную погрешность Δg = ε<g>.

10. Записать конечный результат в виде g = ... ± ... .

Контрольные вопросы

1. Какие колебания называются гармоническими? Дать определение их основных характеристик (амплитуды, фазы, периода, частоты, циклической частоты). При каких условиях колебания физического маятника можно считать гармоническими?

2. Что называется физическим маятником?

3. Вывести формулу периода колебаний физического маятника.

4. Что называется приведенной длиной физического маятника? Вывести формулу (5).

5. Как определить точку подвеса, для которой период колебаний минимальный? Проверьте, соответствует ли расчетное значение экспериментальному?

6. Что называется моментом инерции материальной точки? Как вычислить момент инерции твердого тела? Сформулировать теорему Штейнера.

7. Вывести расчетную формулу (6).

8. Почему для определения g не пользуются непосредственно формулой периода колебаний маятника?