Описание установки и метода Клемана и Дезорма

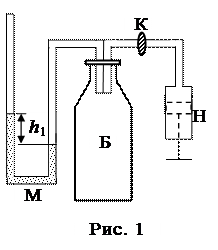Установка состоит из стеклянного баллона Б, поршневого насоса Н, водяного манометра М, клапана-крана К рис. 1. Роль клапана-крана на некоторых установках может выполнять резиновая трубка.

Если при помощи насоса накачать в баллон некоторое количество воздуха, то его давление и температура повысятся. Вследствие теплообмена с окружающей средой температура воздуха в баллоне через некоторое время сравняется с температурой окружающей среды. Давление p₁, установившееся в баллоне, больше атмосферного на величину, определяемую разностью уровней h₁ жидкости в коленах манометра (рис. 1). p и h измеряются в мм водяного столба.

p₁ = p_атм + h₁.

Если обозначить через m массу воздуха в баллоне при атмосферном давлении, то при давлении p₁ воздух займет меньший объем, чем объем сосуда. Обозначим этот объем через V₁. Тогда состояние воздуха массой m внутри баллона будет характеризоваться параметрами p₁, V₁, T₁= T_комн.

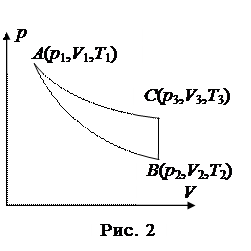
На рис. 2 данному сoстоянию соответствует точка A.

Если открыть на короткое время кран К, то воздух в баллоне расширится. Давление внутри баллона в конце расширения сравняется с атмосферным (обозначим его через p₂ = p_атм, объем рассматриваемой массы воздуха равен объему сосуда V₂. Так как процесс быстрого расширения воздуха можно считать адиабатическим, то температура газа T₂ станет ниже комнатной.

Следовательно, в конце адиабатического расширения (точка B на рис. 2) параметры газа будут p₂, V₂, T₂.

Применяя к этому состоянию уравнение Пуассона, получим:

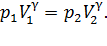
Охладившийся при расширении воздух в баллоне через некоторое время, вследствие теплообмена, нагреется до комнатной температуры (процесс нагревания является изохорическим). Поэтому давление воздуха возрастет до некоторой величины p₃. Это давление будет больше атмосферного на величину, определяемую разностью уровней жидкости в коленах манометра h₂. Параметры этого состояния (точка C на рис. 2):

p₃, V₃, T₃= T_комн, p₃ = p₂ + h₂.

На графике рис. 2 показаны процессы перехода газа из одного состояния в другое. Линия AB является адиабатой, BC – изохорой, AC – изотермой.

Так как переход газа из состояния A в состояние B происходит адиабатически, то он подчиняется уравнению Пуассона ( 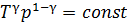), которое в данном случае удобно записать в форме

Дальнейший переход из состояния B в состояние C может быть охарактеризован уравнением Гей-Люссака (изохорический процесс):

Исключив из уравнений (6) и (7) температуру и учтя, что T₁= T₃, получим

Подставляя в (8) значения давлений p₁ и p₃, выраженные через давление p₂ и разность столбов жидкости в манометре (p₁ = p₂ + h₁, p₃ = p₂ + h₂), получим

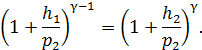
В условиях эксперимента h₁/p₂и h₂/p₂ значительно меньше единицы, поэтому можно ограничиться лишь двумя первыми членами биномов Ньютона, что дает

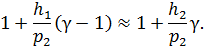
Отсюда можно получить расчетную формулу для коэффициента Пуассона:

Порядок выполнения работы.

1. Проверить, нет ли утечки газа из баллона. Для этого с помощью поршневого насоса медленно нагнетают в баллон воздух. За повышением давления воздуха в баллоне наблюдают по разности уровней в коленах манометра. Так как при нагнетании воздуха температура его несколько повысится, следует подождать 2-3 минуты, пока установится тепловое равновесие с окружающей средой. После этого, если показания манометра не изменяются (нет утечки воздуха), записывают значение h₁, соответствующее исходному состоянию (A).

2. Открыть клапан-кран (К), соединяя воздух в баллоне с атмосферой. Как только выровняется давление воздух внутри баллона с атмосферным (прекратится шипение воздуха), клапан-кран быстро закрыть, или при отсутствии клапана-крана пережать резиновую трубку.

Предполагается, что этот процесс соответствует адиабате АВ (рис. 2). Давление воздуха в баллоне понизится до атмосферного, а газ охладится. Однако, в результате теплообмена с окружающей средой через 2-3 минуты после закрытия клапана-крана газ изохорически перейдет в состояние C. Давление воздуха в баллоне возрастет и появится разность уровней h₂в коленах манометра. Указанный эксперимент повторить 5-6 раз. Результаты измерений h₁ и h₂ записать в табл. 1.

3. По формуле (9) вычислить 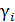для каждого опыта.

4. Вычислить абсолютную и относительную погрешность по формуле:

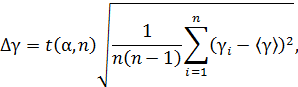
Таблица 1

Номер опыта	h1i	h2i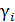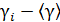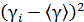

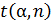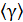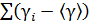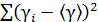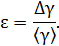
5. Записать конечный результат в виде:

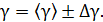
6. Рассчитать 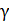теоретически, считая воздух двухатомным газом. Сравнить экспериментальный результат с теоретическим. Объяснить расхождение результатов.

Контрольные вопросы

1. Что называют удельной теплоемкостью и молярной теплоемкостью вещества? Какая связь между ними?

2. Теплоемкость – это функция состояния или функция процесса?

3. Чему равны молярные теплоемкости идеальных газов при изопроцессах?

4. Почему 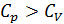? Каков физический смысл универсальной газовой постоянной R?

5. Какое практическое значение имеет соотношение .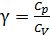

6. Какой процесс называется адиабатическим и каким уравнением он описывается?

7. Какова связь между параметрами, характеризующими состояние газа при адиабатическом процессе?

8. Изобразите график процессов, происходящих в данной работе, в координатах p и V и назовите эти процессы. Изобразите графики известных вам процессов в координатах p и Т, Т и V.

9. От каких параметров зависит внутренняя энергия идеального газа?

10. Как формулируется первое начало термодинамики и как оно записывается аналитически? Как записать его для различных изопроцессов?

11. Выведите расчетную формулу для вычисления .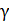

12. Почему необходимо выждать некоторое время после того, как накачают воздух в баллон?

13. Почему после выхода воздуха из баллона и перекрытия клапана-крана возникающая разность уровней в коленах манометра зависит от скорости (времени) расширения газа?

14. Каковы отличия между реальным и идеальным газами?