Отступление от законов идеальных газов. Реальные газы. Изотермы Ван-дер-Ваальса. Критическое состояние (точка)
С ростом давления постепенно поведение реальных газов начинает отличаться от поведения газов идеальных, и при достаточно больших давлениях это отличие становится принципиальным.
Рассмотрим некоторую экспериментальную изотерму (Рис.7.6). (Впервые получена Эндрюсом).
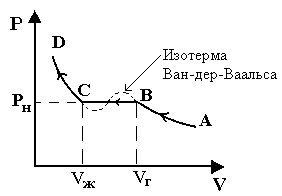 АВ - переход пара из ненасыщенного состояния в насыщенное.
АВ - переход пара из ненасыщенного состояния в насыщенное.
Насыщенный пар – пар, находящийся в динамическом равновесии со своей жидкостью.
ВС - конденсация пара (Рн = const). На этом участке вещество существует в двух агрегатных состояниях: жидком и газообразном. В точке С весь пар превращается в жидкость.
Рис.7.6. CD - жидкое состояние.
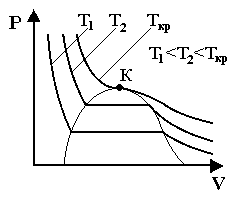 Рассмотрим ряд экспериментальных изотерм, полученных для различных температур (Рис.7.7). Из их графиков видно, что с ростом Т горизонтальный участок уменьшается, стягиваясь в точку. Если через крайние точки горизонтальных участков изотерм провести кривую, то получим приблизительно параболу.
Рассмотрим ряд экспериментальных изотерм, полученных для различных температур (Рис.7.7). Из их графиков видно, что с ростом Т горизонтальный участок уменьшается, стягиваясь в точку. Если через крайние точки горизонтальных участков изотерм провести кривую, то получим приблизительно параболу.
Верхняя точка кривой (точка К) называется критической, она соответствует критическому состоянию, а параметры, этого состояния называют критическими.
Кривая, проходящая через точку К, называется критической кривой (изотермой).
Рис.7.7.
Критическое состояние вещества -состояние, при котором исчезает всякое различие между жидкостью и ее насыщенным паром.
Очевидно, что реальные газы не подчиняются уравнению состояния идеального газа (уравнению Менделеева - Клапейрона), т.к. последнее не учитывает:
1. Размеры молекул (например, при р = 500 МПа объем, занимаемый самими молекулами, равен 0,5 объема, занимаемого газом) .
2. Сил взаимодействия между молекулами.
Ван-дер-Ваальс ввел соответствующие поправки в уравнение состояния идеального газа:
1). Фактически свободный объем, в котором могут двигаться молекулы, (например, для 1 моля газа) будет не Vm , а ( Vm - b ), где b - объем, занимаемый самими молекулами.
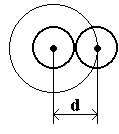 Сталкиваясь, две молекулы сближаются на расстояние d, равное эффективному диаметру (Рис.7.8). Для центров обеих молекул недоступен сферический объем радиуса d, т.е. объем, превышающий объем одной молекулы в восемь раз (объем недоступной сферы
Сталкиваясь, две молекулы сближаются на расстояние d, равное эффективному диаметру (Рис.7.8). Для центров обеих молекул недоступен сферический объем радиуса d, т.е. объем, превышающий объем одной молекулы в восемь раз (объем недоступной сферы 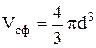 , объем одной молекулы
, объем одной молекулы
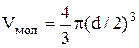 , откуда
, откуда 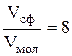 ).
).
Рис.7.8.
В расчете на одну молекулу, недоступным оказывается объем равный учетверенному объему одной молекулы. Для всех молекул, содержащихся в одном моле, - учетверенному собственному объему молекул 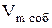 :
:

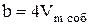 .
.
Отметим, что фактически учет размеров молекул означает учет сил отталкивания. Поэтому данная поправка должна трактоваться как поправка на силы отталкивания.
2). При значительном сближении силы отталкивания превосходят силы притяжения. Однако, как правило, рассматриваются достаточно большие расстояния между молекулами, на которых, в основном, действуют силы притяжения. Их действие приводит к появлению дополнительного давления в газе, которое называется внутренним давлением pi . По расчетам Ван-дер-Ваальса
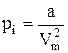 , (7.7.1)
, (7.7.1)
где а - постоянная Ван-дер-Ваальса, Vm - молярный объем.
Уравнение Менделеева - Клапейрона для 1 моля идеального газа имеет вид: pVm = RT .
По Ван-дер-Ваальсу: 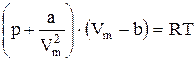 . (7.7.2.)
. (7.7.2.)
Для произвольного количества газа 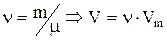 , поэтому, умножая обе части предыдущего уравнения на
, поэтому, умножая обе части предыдущего уравнения на 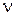 имеем:
имеем:
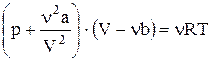 , (7.7.3.)
, (7.7.3.)
где a и b - постоянные, для данного газа – свои. Их, как правило, определяют из эксперимента.
Необходимо отметить, что
1) Уравнение Ван-дер-Ваальса достаточно хорошо описывает участки АВ и CD экспериментальной изотермы. Поведение же реального газа на участке BC уравнению Ван-дер-Ваальса не подчиняется (см.рис.7.6).
2) Существуют и другие уравнения, которые более точно, чем уравнение Ван-дер-Ваальса описывают поведение реальных газов.
