Характеристики электростатического поля

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Методические указания

к лабораторным работам по физике

№ 10, 12, 13, 15, 16, 19 для студентов I и II курсов

всех факультетов

Новосибирск

УДК 537.8 (076.5)

Э 454

Составители:

П.А. Крапивко (приложение),

А.В. Морозов (лаб. работы № 12, 13, 15, приложение),

Б.Л. Паклин (лаб. работа № 10),

А.М. Погорельский (лаб. работы № 15, 16),

Н.П. Потапов (лаб. работа № 19),

О.Ю. Рубцова (лаб. работа № 12),

Н.Я. Усольцева (лаб. работа № 13),

В.В. Христофоров (лаб. работы № 13, 15, 16),

А.А. Шевченко (лаб. работы №12, 13, 15, приложение).

Разработка и изготовление лабораторных установок:

А.М. Погорельский, А.В. Морозов, А.А. Шевченко, П.А. Крапивко

Подготовка к изданию: В.В. Христофоров

Рецензент: А.В. Баранов

Работа подготовлена на кафедре общей физики

Ó Новосибирский государственный

технический университет, 2006

ОГЛАВЛЕНИЕ

Лабораторная работа № 10. ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИ-

ЧЕСКОГО ПОЛЯ............................................................................................. 4

Лабораторная работа № 12. МЕТОДЫ ЭЛЕКТРИЧЕСКИХ

ИЗМЕРЕНИЙ.................................................................................................. 12

Лабораторная работа № 13. ИЗУЧЕНИЕ РАБОТЫ ИСТОЧНИКА ЭДС......... 18

Лабораторная работа № 15. ОПРЕДЕЛЕНИЕ ИНДУКТИВНОСТИ

СОЛЕНОИДА................................................................................................ 25

Лабораторная работа № 16. ВЗАИМНАЯ ИНДУКЦИЯ,

ТРАНСФОРМАТОР...................................................................................... 37

Лабораторная работа № 19. ИЗУЧЕНИЕ ПЕТЛИ ГИСТЕРЕЗИСА

И ИЗМЕРЕНИЕ ПАРАМЕТРОВ ФЕРРОМАГНЕТИКОВ................... 46

Лабораторная работа № 10

ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

Цель работы – построение эквипотенциальных линий электростатического поля с помощью экспериментального моделирования в проводящей среде, в которой протекает переменный ток.

Характеристики электростатического поля

Если в пространстве имеется система заряженных тел, то в каждой точке этого пространства существует силовое электростатическое поле, которое определяется через силу, действующую на «пробный» заряд в данной точке пространства. «Пробный» заряд q₀ должен быть точечным и достаточно малым по величине, чтобы не вносить существенных искажений в силовое поле, созданное системой зарядов. Чтобы напряженность электростатического поля 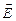не зависела от величины «пробного» заряда, её определяют как отношение силы, действующей на «пробный» заряд, к величине этого заряда:

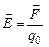. (10.1)

Напряженность – силовая характеристика электрического поля.

Электростатическое поле можно представить графически в виде силовых линий, называемых линиями напряженности. Вектор напряженности 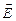в каждой точке такой линии, направлен по касательной к ней и совпадает с ней по направлению. Густота линий характеризует величину напряженности электростатического поля. Вблизи точечных зарядов эти линии сгущаются и напряженность 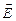возрастает. Направление электростатического поля, как видно из (10.1), совпадает с направлением силы, действующей на положительный заряд в данной точке пространства. Силовые линии 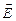начинаются на положительных и заканчиваются на отрицательных зарядах или уходят на бесконечность. Силовые линии электростатического поля незамкнуты. Сила, действующая на точечный заряд величиной q, полностью определяется величиной самого заряда и напряженностью электростатического поля в данной точке пространства

.

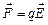Для вектора 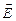выполняется принцип суперпозиции: напряженность поля, созданного несколькими зарядами, равна векторной сумме напряженностей, создаваемых каждым из зарядов в отдельности

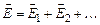(10.2)

Так как силы взаимодействия двух точечных зарядов направлены вдоль линии их соединяющей и зависят лишь от расстояния между ними, то сила, действующая на заряд, помещенный в электростатическое поле, является центральной и, следовательно, консервативной. Вследствие этого работа по перемещению заряда в электростатическом поле не зависит от траектории движения, а определяется лишь начальным и конечным положениями заряда на этой траектории. Поэтому стационарное электростатическое поле является потенциальным.

В каждой точке такого поля можно, кроме силовой характеристики, ввести энергетическую характеристику – потенциал j. При перемещении «пробного» заряда q₀ из точки 1 с потенциалом j₁ в точку 2
с потенциалом j₂ по произвольному пути силами электростатического поля совершается работа

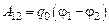. (10.3)

Следовательно, разность потенциалов между точками 1 и 2
(j₁ – j₂)можно определить как отношение работы сил поля А₁₂ к величине заряда q₀

.

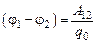При бесконечно малом перемещении 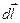заряда в произвольном направлении силой поля совершается элементарная работа 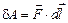, где 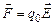. С другой стороны, эту работу можно выразить через приращение потенциала: 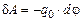. Тогда, сокращая на q₀ и приравнивая работы, получаем

.

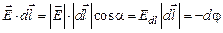Таким образом, установлена связь между проекцией вектора 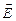на направление перемещения 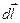и потенциалом j электрического поля

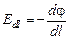. (10.4)

С помощью последнего выражения выразим вектор 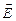через потенциал. При этом учтем, что

,

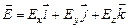где 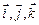– орты осей 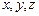соответственно.

Согласно (10.4)

.

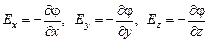Следовательно, для вектора 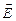можно записать

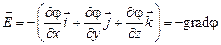, (10.5)

т. е. вектор напряженности электростатического поля равен градиенту его потенциала со знаком «минус». Вводя оператор набла

,

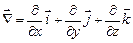эту же связь можно представить в виде

.

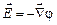Итак, силовая 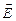и энергетическая j характеристики электростатического поля связаны друг с другом.

Поверхности равного потенциала j = const называются эквипотенциальными. Из соотношения 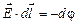следует, что при перемещении заряда вдоль эквипотенциальной поверхности работа электростатического поля равна нулю, что возможно только тогда, когда вектор напряженности 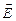перпендикулярен к этой поверхности. Поскольку вектор 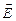направлен вдоль касательной к силовой линии, это означает, что силовые линии пересекают эквипотенциальные поверхности под прямым углом.

Метод измерений

В слабо проводящую среду, которую представляет собой недистиллированная вода, помещают два металлических проводника, подсоединенных к источнику переменного тока. Так как проводимость среды намного меньше проводимости помещенных в нее металлических электродов, то потенциал в разных точках этих электродов с достаточной степенью точности можно считать одинаковым. При этом топография поля в пространстве между ними будет такой же, какой была бы топография электростатического поля между заряженными проводниками, помещенными в однородную непроводящую среду.

В проводящей среде выполняется закон Ома 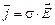, здесь 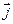– вектор плотности тока, s – удельная электропроводность (проводимость) среды.

Метод моделирования электростатического поля в проводящей среде основан на аналогии уравнений, описывающих электрическое поле в вакууме и в изотропной проводящей среде. Метод удобен на практике, так как позволяет получить путем экспериментального моделирования сложную картину электростатического поля, аналитический расчет которого зачастую невозможен из-за сложности граничных условий. Использование переменного тока позволяет предотвратить выделение на электродах составных частей электролита. Для переменного синусоидального тока в электролите переменное электрическое поле не является потенциальным, в каждой точке напряжение изменяется со временем. Однако понятие эквипотенциальной поверхности как поверхности постоянно изменяющегося со временем, но одинакового по амплитуде потенциала можно считать справедливым. Разные эквипотенциальные поверхности при этом характеризуют неодинаковые амплитуды переменного напряжения. Напряжение любой точки внутри электролитической ванны относительно одного из электродов легко измерить вольтметром. Эти измерения позволяют определить местоположение и форму эквипотенциальных линий поля, созданного в ванне.

По картине эквипотенциальных линий можно построить соответствующую картину силовых линий. Кроме того, по картине эквипотенциальных линий, пользуясь формулой (10.4), можно оценить численное значение напряженности электрического поля в любом месте ванны. При этом следует учесть, что проекция вектора на его собственное направление равна модулю этого вектора и по величине максимальна. Из формулы (10.4) видно, что если в некоторой точке ванны найти минимальное расстояние 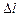между двумя ближайшими эквипотенциальными линиями с известными потенциалам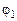и и 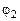, то отношение 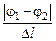будет максимальным, а следовательно, равным модулю вектора напряженности электрического поля в этом месте ванны,

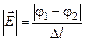. (10.6)