Работа газа при изменении его объема

Если газ, расширяясь, двигает поршень на расстояние dl, то он совершает над поршнем работу

dA = Fdl = pSdl = pdV, (2)

где S - площадь поршня, dV = Sdl - изменение объема системы (рис.1).

Полная работа, совершаемая газом при изменении его объема от V₁ до V₂, равна A = 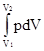, (2a)

и результат интегрирования определяется зависимостью p(V). Произведенную работу можно изобразить графически в координатах p-V (рис.2): элементарная работа dA определяется заштрихованной полосой на рисунке, а полная работа - площадью, ограниченной кривой p(V) и прямыми V₁ и V₂.

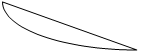
Для графического изображения термодинамических процессов можно использовать также диагрaммы p-T и V-T. Графически можно изображать только равновесные процессы - они протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало. Все реальные процессы неравновесные, но в ряде случаев этой неравновесностью можно пренебречь (чем медленнее протекает процесс, тем ближе он к равновесному).

p

p S

V

dl Рис.1. V₁ dV V₂ Рис.2.

Теплоемкость

3.4.1. Удельная теплоемкость- величина, равная количеству теплоты, необходимому для нагрева 1 кг вещества на 1К: с = dQ/mdT, где m - масса вещества, единица удельной теплоемкости [Дж/(кг^.К)].

3.4.2. Молярная теплоемкость - величина, равная количеству теплоты, необходимому для нагрева 1 моль вещества на 1К: C_m = dQ/ndT, где n = m/M - количество вещества, М - молярная масса.

Связь между C и C_m: C_m = сM.

3.4.3. Молярная теплоемкость при постоянном объеме(в процессе нагревания вещества его объем поддерживается постоянным) C_V = (dQ/ndT)_V.

Первое начало для 1 моль газа можно записать С_mdT = dU_m + pdV_m. (*)

Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю А = pdV = 0 и сообщаемая извне теплота идет только на увеличение внутренней энергии, так что первое начало (*) можно записать C_V = dU_m/dT - молярная теплоемкость при постоянном объеме - она равна изменению внутренней энергии 1 моль газа при повышении его температуры на 1 К. Из выражения dU_m = (iR/2)dT получаем C_V = iR/2.

3.4.4. Молярная теплоемкость при постоянном давлении(в процессе нагревания вещества его давление поддерживается постоянным) C_p = (dQ/ndT)_p

Если газ нагревается при постоянном давлении, то первое начало можно записать в виде C_p = dU_m/dT +(pdV_m/dT),

причем, дифференцируя уравнение Клапейрона-Менделеева pV_m = RT по Т (при p=const), получим уравнение Майера

C_p = C_V + R, т.е. С_p всегда больше, чем C_V - это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа (т.к. постоянство давления обеспечивается увеличением объема газа).

Учитывая, что C_V = iR/2, получим C_p = (i+2)R/2, а также соотношение g = C_p/C_V = (i+2)/i.

Наиболее важный вывод - молярные теплоемкости идеального газа определяются лишь числом степеней свободы и не зависят от температуры. Этот вывод справедлив и для реальных одноатомных газов. Однако для реальных многоатомных газов число степеней свободы зависит от температуры (при низких температурах проявляется только поступательное движение, а при более высоких добавляется вращательное движение, а при очень высоких добавляется еще и колебательное движение) и, следовательно, теплоемкости также зависят от температуры.