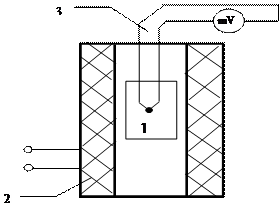
Описание экспериментальной установки. Схема лабораторной установки приведена на рис.2

Схема лабораторной установки приведена на рис.2. Ампула с оловом 1 нагревается в электрической печи 2. Внутри ампулы находится металлическая трубка - чехол с термопарой 3 «хромель – копель», спай которой находится в ампуле. Концы термопары через гнезда и провода соединены с милливольтметром, измеряющим термоэ.д.с -.ε. Электрическая печь находиться в модуле стенда. Подключение электрической печи к сетевым разъемам стенда производится вилкой подводящих проводов 4.

Рис. 2

Порядок выполнения работы

1. Зарисовать таблицу и занести в нее данные установки.

Температура воздуха в лаборатории - Т₁ – К Таблица .

Масса олова m=(данные на установке), кг Удельная теплоемкость олова сv=0,243 (Дж/К×кг)	Масса ампулы m1=(данные на установке), кг Удельная теплоемкость материала ампулы cv1=0,46 (Дж/К×кг)
№	e, мВ	q, К	Т, К	t, с
1. 2. ...

2. Включить стенд, милливольтметр, электрическую печь.

3. Проследить в течении некоторого времени за тем, чтобы олово находящееся в ампуле расплавилось. Процесс плавления олова происходит при постоянной температуре плавления. При этом показания милливольтметра практически не меняются. Окончание процесса плавления можно определить как момент времени, после которого показания милливольтметра начинают возрастать.

4. Через 1 минуту после окончания процесса плавления отключить электрическую печь. Милливольтметр должен показывать ~ 13 мВ. Т.к. процесс нагревания обладает инерционностью, то некоторое время показания милливольтметра будут расти, а затем начнут уменьшаться.

5. При ε = 14 мВ включить секундомер и через каждые 10 секунд снимать показания милливольтметра. Данные занести в таблицу.

6. Измерение ε продолжать до тех пор, пока не будут пройдены три области процесса охлаждения, область полного расплава; область кристаллизации; область охлаждения твердого олова. Время опыта - около 10 минут. Получив 30 - 40 экспериментальных точек, выключить милливольтметр и стенд.

Обработка результатов измерений

1. Используя зависимость e = kθ, где k = 0.667мВ/К, θ = Т-Т₁ , определить разность температур олова и окружающей среды для зафиксированных моментов времени. Рассчитать соответствующие значения Т. Данные занести в таблицу.

2. Построить диаграмму отвердевания олова и по ней определить:

а) температуру кристаллизации олова Т_кр;

б) время фазового перехода t_ф.п.;.

в) скорость охлаждения образца 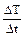(область расплава), выделив прямолинейный участок диаграммы в близи области фазового перехода.

3. По формуле (3) вычислить удельную теплоту кристаллизации олова.

4. По формуле (8) вычислить изменения энтропии в процессе кристаллизации олова.

8. Рассчитать погрешности l и Т_кр и сравнить полученные значения l и Т_кр с табличными значениями.

9. Сделать выводы.

Контрольные вопросы

1. Что такое фаза, фазовый переход?

2. Что такое фазовый переход первого рода?

3. Чем отличается фазовый переход первого рода от фазового перехода второго рода?

4. Из чего складывается внутренняя энергия твердого тела?

5. Объясните процессы плавления и кристаллизации.

6. Почему температура тела при плавлении и кристаллизации остается постоянной?

7. Расплавится ли тело, если его нагреть до температуры плавления?

8. Нарисуйте диаграмму плавления и дайте характеристику происходящим процессам.

9. Выведите формулу (3).

10. Что такое энтропия? Сформулируйте физическое содержание этого понятия.

11. В чем заключается статистический смысл энтропии?

12. Как меняется энтропия при плавлении, при кристаллизации?

13. Укажите возможные погрешности измерений.

Лабораторная работа № 4

Измерение отношения изобарной и изохорной теплоёмкостей газа

Цель работы: измерение отношения изобарной и изохорной теплоемкостей воздуха.

Введение

По первому началу термодинамики, сообщенное газу количество теплоты dQ расходуется на увеличение внутренней энергии газа dU и совершение газом работы dA:

dQ = dU+dA

Количество теплоты, необходимое для нагревания газа, зависит от количества нагреваемого газа и от того, на сколько градусов должна быть изменена его температура. Чем больше то и другое, тем больше потребное количество теплоты. Поэтому для характеристики тепловых свойств газа, как и всякого другого тела, пользуются особой величиной - теплоемкостью.

Теплоемкостью тела C называется количество тепла, которое нужно подвести к нему или отнять от него для изменения его температуры на 1 К:

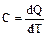
Теплоемкость, отнесенная к единице массы вещества, называется удельной теплоемкостью. Она характеризует уже не тело, а вещество, из которого состоит тело, и обозначается буквой с :

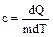
Теплоемкость, отнесенная к одному молю вещества, называется молярной теплоемкостью. Как и удельная теплоемкость, она является характеристикой вещества и обозначается С_μ:

,

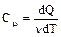где m - молярная масса вещества.

Между удельной теплоемкостью и молярной существует очевидное соотношение:

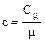,(1)

Если моль вещества нагревается на dT градусов, то количество теплоты, затрачиваемое на это, равно:

dQ = C_μ dT,

Пусть нагревание происходит в условиях, когда объем остается постоянным (V=сonst).Соответствующая молярная теплоемкость называется теплоемкостью при постоянном объеме, или изохорной теплоемкостью, и обозначается С_V:

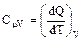
Так при постоянном объеме работа газом не совершается, то теплота тратиться только на изменение внутренней энергии:

dQ = dU

и

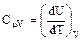
Если при нагревании постоянным остается давление (Р = const.), то теплоемкость называется теплоемкостью при постоянном давлении, или изобарной теплоемкостью,и обозначается C_μр:

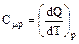
Учитывая, что 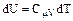и 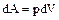первое начало термодинамики можно переписать в виде:

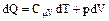
Теплоемкость C_μр идеального газа при постоянном давлении больше теплоемкости при постоянном объеме С_μV на величину работы, которую совершает моль газа, расширяясь при нагревании на 1К. Работа эта равна 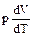. Таким образом:

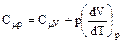
Но для моля идеального газа рV=RT и поэтому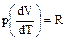

C_μр = C_μV + R

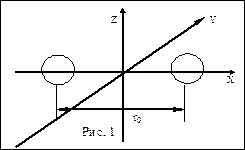
Внутренняя энергия идеального газа складывается из средних кинетических энергии всех молекул газа. Средняя кинетическая энергия молекул зависит от числа степеней свободымолекул. Числом степеней свободы механической системы называется число независимых координат, определяющих ее положение и конфигурацию в пространстве. Например, двухатомную молекулу можно себе представить в виде системы, состоящей из двух атомов, расположенных на некотором расстоянии r₀ друг от друга (рис.1). Если расстояние между этими атомами не меняется (такие молекулы называются жесткими), то такая система имеет пять степеней свободы.

Действительно, конфигурация и положение такой молекулы определяются: тремя координатами ее центра масс, которыми определяется поступательное движение молекулы как целого и тремя координатами, определяющими возможные вращение молекулы около взаимно перпендикулярных осей X,Y,Z. Однако опыт и теория показывают, что вращение около оси Х не приводит к изменению положения молекулы, поэтому для описания возможных вращений молекулы достаточно двух координат. Таким образом, число степеней свободы жесткой двухатомной молекулы i = 5 (три поступательные, две вращательные).

Но атомы в молекуле не всегда жестко связаны друг с другом; они могут совершать колебания друг относительно друга при высоких температурах (≤ 1000 К). Тогда требуется еще одна координата для определения конфигурации молекулы; это - расстояние между атомами. Следовательно, в общем случае двух атомная молекула обладает шестью степенями свободы: тремя поступательными, двумя вращательными и одной колебательной.

В классической статистической физике доказывается закон равномерного распределения кинетической энергии по степеням свободы молекулы (закон Больцмана): если система молекул находится в тепловом равновесии при температуре Т, то средняя кинетическая энергия равномерно распределяется между всеми степенями свободы и для каждой степени свободы молекулы она равна 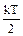. Исключения составляет лишь колебательная степень свободы на которую приходятся энергия равная kТ. Для низких температур (не превышающих 1000 К) средняя энергия теплового движения молекулы равна 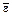= i 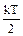. Число степеней свободы определяются как:

i = i_пост + i_вращ+ i_кол,

где i_пост - число поступательных степеней свободы, i_вращ – число вращательных степеней свободы, i_кол – число колебательных степеней свободы.

Внутренняя энергия одного моля газа по определению равна:

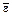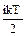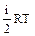U = N_A∙ =N_A = . (1)

Соответственно этому, молярные теплоемкости газа:

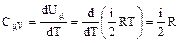
и

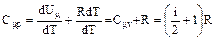
Тогда отношение теплоемкостей равно:

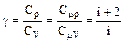(2)

Отношение теплоемкости газа g входит в уравнение Пуассона 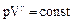. Это уравнение описывает адиабатический процесс, т.е. процесс, протекающий без теплообмена с окружающей средой. К адиабатическим процессам близки все быстропротекающие процессы. Например, адиабатическим можно считать процесс мгновенного расширения газа в вакуум или процесс распространения в упругой среде звуковых волн.