По скорости звука в воздухе

Цель работы: определить коэффициент Пуассона для воздуха, измеряя методом стоячей волны скорость распространения звука в воздухе.

Методика эксперимента

В настоящей работе необходимо определить экспериментально адиабатическую постоянную (коэффициент Пуассона) 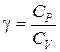для воздуха. Один из способов определения g основан на измерении скорости звука в газе. Как известно из теории, скорость звука v в газе определяется формулой

v = 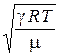, (3.21)
где R = 8,31 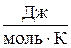- универсальная газовая постоянная; Т – абсолютная температура; m - молярная масса газа.

Из уравнения (3.21) определяем коэффициент Пуассона

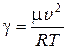, (3.22)

следовательно, определив экспериментально v, можно найти g.

Схема установки для определения скорости звука приведена на рис. 3.9.

На одном из концов стеклянной трубы Тр укреплен телефон Т, создающий с помощью звукового генератора ЗГ колебания заданной частоты. Вдоль трубы перемещается поршень П, в который вмонтирован микрофон М.

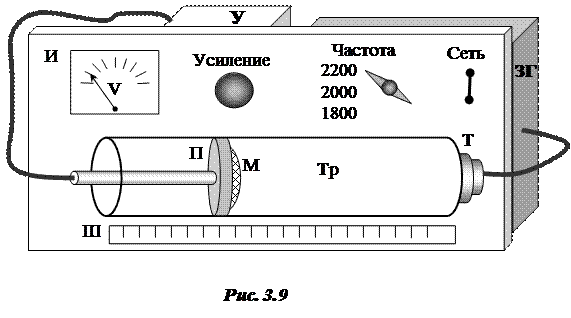
Колебания мембраны телефона передаются воздуху, и вдоль трубы начинает распространяться звуковая волна. Звук улавливается микрофоном, положение которого относительно мембраны телефона определяется по шкале Ш.

Громкость звучания столба воздуха в трубе определяется на слух или с помощью индикатора И (через усилитель У).

Возбуждая колебания определенной частоты с помощью звукового генератора ЗГ и перемещая поршень П в трубе, находят положения, соответствующие максимальному звуковому сигналу – x₁, x₂,…, x_n.

Расстояния между точками, соответствующими максимальному звуковому сигналу

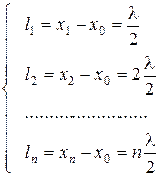, (3.23)
где x₀ – координата начала трубы, l - длина звуковой волны.

Из выражения(3.23) следует: .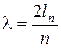

Известно, что длина волны l связана с частотой n соотношением

,

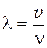тогда ,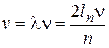

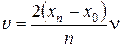, (3.24)
где n = 1, 2, 3,… - число пучностей (положений поршня, соответствующих максимальному звучанию сигнала).

Порядок выполнения работы

1. Включить звуковой генератор ЗГ и индикатор напряжения И в сеть 220В. Прогреть 1 – 3 минуты.

2. Установить регулятор переключения частоты на 2000 Гц.

3. Перемещая поршень вдоль трубы, сосчитать число пучностей (максимальный звуковой сигнал), укладывающихся по всей длине трубки – n.

4. Измерить по линейке положение последней пучности – x_n и координату начала трубы – x₀.

5. Повторить пункты 2 - 4 с другими, указанными на панели прибора, частотами.

6. Снять показания температуры Т в лаборатории по термометру.

Результаты измерений занести в таблицу 3.3.

Таблица 3.3

n	x0, см	xn, см	n	Т, К	постоянные
					m = 29×10-3 кг/моль R = 8,31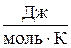

Обработка результатов измерений

1. По формуле (3.24) рассчитать скорость звука в воздухе, используя данные таблицы измерений, выраженные в единицах СИ.

2. По формуле (3.22) найти значение коэффициента Пуассона для воздуха.

3. Сравнить полученное значение коэффициента Пуассона с теоретическим. Сделать вывод по проделанной работе.

Контрольные вопросы и задания

1. Сформулируйте первое начало термодинамики.

2. Как определяется внутренняя энергия системы? Запишите выражение для внутренней энергии идеального газа.

3. Что такое число степеней свободы? Как определяется это число для одно-, двух- и трехатомных молекул?

4. Что называется удельной и молярной теплоёмкостями?

5. Какие физические величины обозначаются знаками С_Р и С_V? Каким уравнением описывается связь между ними? Какие законы используются при выводе этого уравнения?

6. Какой процесс называется изотермическим? Изобарическим? Изохорическим? Адиабатическим? Запишите уравнения состояния для этих процессов.

7. Запишите первое начало термодинамики для всех изопроцессов и для адиабатического процесса.

Свойства жидкостей

Поверхностное натяжение

Жидкость является агрегатным состоянием вещества, промежуточным между газообразным и твёрдым и, соответственно, обладает свойствами и тех и других. Жидкости, подобно твёрдым телам, обладают определённым объёмом и, подобно газам, принимают форму сосуда, в котором они находятся.

Молекулы газа практически не связаны между собой силами межмолекулярного взаимодействия. в данном случае средняя энергия теплового движения молекул газа гораздо больше средней потенциальной энергии, обусловленной силами притяжения между ними, поэтому молекулы газа разлетаются в разные стороны, и газ занимает предоставленный ему объём. В твёрдых и жидких телах силы притяжения между молекулами уже существенны и удерживают молекулы на определённом расстоянии друг от друга. В этом случае средняя энергия хаотического теплового движения молекул меньше средней потенциальной энергии, которая обусловлена силами межмолекулярного взаимодействия, и её недостаточно для преодоления сил притяжения между молекулами, поэтому твёрдые тела и жидкости имеют определённый объём.

В газах молекулы движутся хаотично, поэтому нет никакой закономерности в их взаимном расположении. В жидкостях, в отличие от твёрдых тел, имеет место так называемый ближний порядок в расположении частиц – их упорядоченное расположение, повторяющееся на расстояниях, сравнимых с межатомными. Тепловое движение в жидкости объясняется тем, что каждая молекула в течение некоторого времени колеблется около определённого положения равновесия, после чего скачком переходит в новое положение, отстоящее от исходного на расстоянии порядка межатомного. Таким образом, молекулы жидкости довольно медленно перемещаются по всей массе жидкости, и диффузия происходит гораздо медленнее, чем в газах. С повышением температуры жидкости частота колебательного движения молекул резко увеличивается, возрастает подвижность молекул, что в свою очередь является причиной уменьшения вязкости жидкости.

На границе раздела двух веществ, например, таких как жидкость и её насыщенный пар, две несмешиваемые жидкости или жидкость и твёрдое тело возникает сила, обусловленная различным межмолекулярным взаимодействием граничащих сред. Все молекулы, расположенные внутри объёма жидкости, равномерно окружены соседними молекулами, при этом, равнодействующая всех сил, действующая на любую такую молекулу, усредняется до нуля. С другой стороны, на молекулу, находящуюся вблизи границы двух сред, вследствие неоднородности окружения действует сила, не скомпенсированная другими молекулами жидкости.

На каждую молекулу жидкости со стороны окружающих молекул действуют силы притяжения, быстро убывающие с расстоянием (рис 4.1).

Соотношение между минимальной потенциальной энергией и средней кинетической энергией хаотического теплового движения, примерно равной kT, определяет возможность существования того или иного агрегатного состояния вещества (рис. 4.2.):

Е_{п min} << kT - вещество находится в газообразном состоянии;

Е_{п min} >> kT - вещество находится в твердом состоянии;

Е_{п min} » kT - вещество находится в жидком состоянии.

При r = r₀ потенциальная энергия достигает минимального значения, что соответствует состоянию устойчивого равновесия этой системы. При r < d (d - эффективный диаметр молекулы) потенциальная энергия, обусловленная силами отталкивания, резко возрастает, что препятствует дальнейшему сближению молекул.

Начиная с некоторого минимального расстояния силами притяжения между молекулами можно пренебречь. Это расстояние (r ≈ 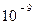м) называется радиусом молекулярного действия, а сфера радиуса r – сферой молекулярного действия. На молекулы поверхностного слоя жидкости, сферы молекулярного действия которых лишь частично расположены в жидкости, действуют силы, направленные внутрь жидкости, оказывая давление, называемое молекулярным или внутренним. Молекулярное давление не действует на тело, помещенное в жидкость, так как оно обусловлено силами, действующими только между молекулами самой жидкости.

Полная энергия частиц жидкости складывается из их хаотического теплового движения и потенциальной энергии, обусловленной силами межмолекулярного взаимодействия. Для перемещения молекулы из глубины на поверхность жидкости надо затратить работу. Данная работа совершается за счёт кинетической энергии молекул и идёт на увеличение их потенциальной энергии. Дополнительная потенциальная энергия молекул поверхностного слоя жидкости называется поверхностной энергией. Так как данная энергия ΔЕ прямо пропорциональна площади слоя ΔS , то: ΔЕ = σ×ΔS, где s –коэффициент поверхностного натяжения жидкости, определяемый как плотность поверхностной энергии.

Другими словами, коэффициент поверхностного натяжения – это величина, равная отношению работы, затраченной на создание некоторой поверхности жидкости при постоянной температуре, к площади этой поверхности.Условием устойчивого равновесия жидкости является минимум поверхностной энергии.

Так же можно дать и силовую характеристику σ: коэффициент поверхностного натяжения жидкостиσравен силе поверхностного натяжения, которая приходится на единицу длины контура, ограничивающего рассматриваемую поверхность жидкости: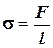 .Если рассмотреть на поверхности жидкости небольшой отрезок длиной l, то силы поверхностного натяжения можно условно изобразить отрезками, перпендикулярными выбранному отрезку (то есть они напоминают “хирургический шов ” на “разрезе” поверхности жидкости).

Единицы измерения коэффициента поверхностного натяжения - ньютон на метр (Н /м) или джоуль на квадратный метр (Дж/м²). Большинство жидкостей при температуре 300 К имеет коэффициент поверхностного натяжения порядка 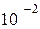- 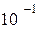Н/м. С повышением температуры поверхностное натяжение уменьшается, так как увеличиваются средние расстояния между молекулами жидкости. Поверхностное натяжение существенно зависит от наличия примесей (например, при температуре 20 °С для воды σ = 0,0725 Н /м, для молока σ = 0,05 Н /м, а для мыльной воды σ ≈ 0,04 Н /м).

Лабораторная работа