Примеры выполнения тестовых заданий
ВВЕДЕНИЕ
Интернет-экзамен позволяет диагностировать и отслеживать уровень подготовки студентов на соответствие требованиям государственных образовательных стандартов (ГОС) высшего профессионального образования (ВПО).
В основе методики оценки качества подготовки студентов является оценка освоения всех дидактических единиц (ДЕ) дисциплины на уровне требований ГОС. Подготовка считается соответствующей требованиям стандарта, если он освоил все контролируемые ДЕ, т. е. правильно выполнил не менее 50% тестовых заданий в каждой ДЕ.
Измерительные материалы предназначены для проверки обязательного (базового) уровня подготовки и предполагают использование знаний и умений в знакомой ситуации, т.е. задания рассчитаны на типовые действия.
При выполнении тестовых заданий студент должен уметь:
1. применять физические законы в условиях конкретной задачи;
2. использовать физические формулы для анализа функциональных зависимостей между различными физическими величинами;
3. использовать физические формулы для вычисления заданных величин;
4. определять направления векторных величин;
5. анализировать информацию, представленную в виде графика, рисунка, делать вывод о характере изменения искомой величины;
6. использовать математический аппарат (вычисление производных, интегралов, операции с векторами) для решения физических задач.
Методические указания предназначены для подготовки к Интернет-экзамену студентов технических специальностей, изучающих дисциплину «Физика» в объеме от 280 до 699 часов, и соответствуют содержанию дисциплины «Физика» в ГОС.
Методические указания составлены на основе структуры АПИМ и включают требования к знаниям и умениям, которые студент должен приобрести в результате освоения отдельных разделов дисциплины, и примеры выполнения тестовых заданий, используемых в качестве измерительных материалов при проведении Интернет-экзамена.
ТЕМАТИЧЕСКАЯ СТРУКТУРА АПИМ
| № ДЕ | Наименование ДЕ | № задан. | Тема задания |
| Механика | Кинематика поступательного и вращательного движения точки | ||
| Динамика поступательного движения | |||
| Динамика вращательного движения | |||
| Работа и энергия | |||
| Законы сохранения в механике | |||
| Элементы специальной теории относительности | |||
| Молекулярная (статистическая) физика и термодинамика | Распределения Максвелла и Больцмана | ||
| Средняя энергия молекул | |||
| Второе начало термодинамики. Энтропия. Циклы | |||
| I начало термодинамики. Работа при изопроцессах | |||
| Электричество и магнетизм | Электростатическое поле в вакууме | ||
| Законы постоянного тока | |||
| Магнитостатика | |||
| Явление электромагнитной индукции | |||
| Электрические и магнитные свойства вещества | |||
| Уравнения Максвелла | |||
| Механические и электромагнитные колебания и волны | Свободные и вынужденные колебания | ||
| Сложение гармонических колебаний | |||
| Волны. Уравнение волны | |||
| Энергия волны. Перенос энергии волной | |||
| Волновая и квантовая оптика | Интерференция и дифракция света | ||
| Поляризация и дисперсия света | |||
| Тепловое излучение. Фотоэффект | |||
| Эффект Комптона. Световое давление | |||
| Квантовая физика, физика атома | Спектр атома водорода. Правило отбора | ||
| Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга | |||
| Уравнения Шредингера (общие свойства) | |||
| Уравнение Шредингера (конкретные ситуации) | |||
| Элементы ядерной физики и физики элементарных частиц | Ядро. Элементарные частицы | ||
| Ядерные реакции | |||
| Законы сохранения в ядерных реакциях | |||
| Фундаментальные взаимодействия |
Механика
Кинематика Поступательного и вращательного движения
При выполнении тестовых заданий студент должен
знать: скорость, ускорение, составляющие ускорения – тангенциальное и нормальное; угловая скорость, угловое ускорение; связь линейных и угловых величин.
уметь: применять законы кинематики в условиях конкретной задачи.
Примеры выполнения тестовых заданий
Задание 1. Материальная точка M движется по окружности со скоростью 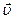 . На рис. 1 показан график зависимости модуля скорости от времени.
. На рис. 1 показан график зависимости модуля скорости от времени.
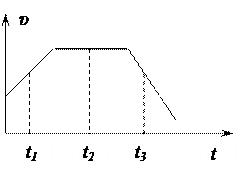
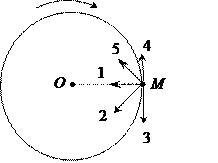
Рис. 1 Рис. 2
При этом вектор полного ускорения в момент времени t3 на рис.2 имеет направление …
Выполнение задания.Как видно из рисунка 1, в интервале времени, включающем момент времени t3, модуль скорости уменьшается, а значит, материальная точка M движется равнозамедленно и тангенциальное ускорение 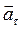 направлено против движения (т.е. в направлении 4). В результате изменения направления скорости возникает нормальное ускорение направлено против движения (т.е. в направлении 4). В результате изменения направления скорости возникает нормальное ускорение 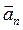 , направленное , направленное | Рис.3 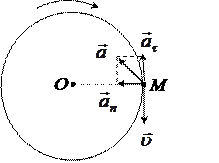 |
к центру окружности (в направлении 1). Полное ускорение равно 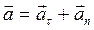 , следовательно, оно имеет направление 5 (рис. 3).
, следовательно, оно имеет направление 5 (рис. 3).
Ответ: 5)
Задание 2.Два тела брошены под одним и тем же углом к горизонту с начальными скоростями υ0 и 2υ0. Если сопротивлением воздуха пренебречь, то соотношение дальностей полета S2/S1 будет равно …
| 1) | 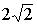 | 2) | 3) | 4) |  |
Выполнение задания.При отсутствии сопротивления воздуха тела будут двигаться под действием только одной силы – силы тяжести с ускорением свободного падения 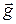 .
.
Движение тела можно представить как суперпозицию (наложение) двух движений: равномерного в направлении оси ох и равнопеременного в направлении оси оу.
Движение тела схематично изображено на рисунке
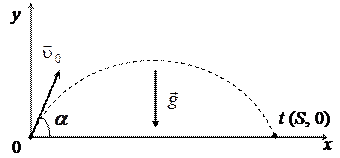
Дальность полета S (координата тела по оси ох в момент времени t) равна
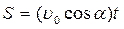 ,
,
а координата тела по оси oy в момент времени t:
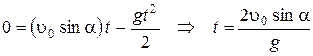 .
.
Решая эту систему уравнений, получим: 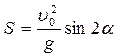 , то есть
, то есть
S ~ 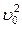 .
.
Следовательно, 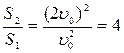 .
.
Ответ: 2) 4
Задание 3.Диск вращается вокруг своей оси, изменяя проекцию угловой скорости 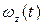 так, как показано на рисунке. Диск вращается равнозамедленно с направлением вектора угловой скорости
так, как показано на рисунке. Диск вращается равнозамедленно с направлением вектора угловой скорости 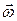 по оси Z в интервалы времени …
по оси Z в интервалы времени …
| 1) | от 0 до t1 | 2) | от t1 до t2 | |
| 3) | от t2 до t3 | 4) | от t3 до t4 |
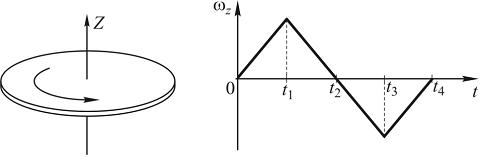
Выполнение задания.На всех интервалах времени проекция угловой скорости wz на ось Z линейно изменяется со временем
wz = w0z + ezt,
следовательно, диск вращается равнопеременно.
Вектор угловой скорости 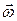 направлен по оси Z, если проекция этого вектора wz на ось положительная. А это происходит в интервалы времени от 0 до t1 и от t1 до t2.
направлен по оси Z, если проекция этого вектора wz на ось положительная. А это происходит в интервалы времени от 0 до t1 и от t1 до t2.
В интервале времени от 0 до t1 проекция углового ускорения 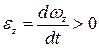 и wz > 0, значит, диск вращается равноускоренно. В интервале времени от t1 до t2,
и wz > 0, значит, диск вращается равноускоренно. В интервале времени от t1 до t2, 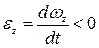 , а wz > 0, следовательно, диск вращается равнозамедленно.
, а wz > 0, следовательно, диск вращается равнозамедленно.
Таким образом, диск вращается равнозамедленно с направлением вектора угловой скорости 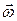 по оси Z в интервале времени от t1 до t2.
по оси Z в интервале времени от t1 до t2.
Ответ: 2) от t1 до t2
Задание 4.Диск радиуса R вращается вокруг вертикальной оси равноускоренно по часовой стрелке. Вектор углового ускорения имеет направление … Выполнение задания.Так как диск вращается равноускоренно, т. е. 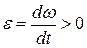 , то направление вектора углового ускорения , то направление вектора углового ускорения 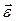 | 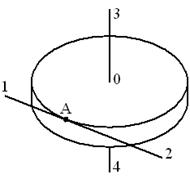 |
совпадает с направлением вектора угловой скорости 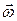 .
.
Вектор угловой скорости 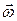 в соответствии с правилом правого буравчика направлен вдоль оси вращения вниз, т.е. в направлении 4, следовательно, и вектор углового ускорения
в соответствии с правилом правого буравчика направлен вдоль оси вращения вниз, т.е. в направлении 4, следовательно, и вектор углового ускорения 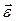 имеет направление 4.
имеет направление 4.
Ответ: 4)
