Искровые газовые разрядники высокого давления

Одним из основных элементов мощных импульсных генераторов являются коммутирующие устройства, позволяющие в нужный момент времени подключить отдельные компоненты этих генераторов к общей схеме. Эти устройства должны выдерживать высокое напряжение (свыше ~100 кВ), быстро включаться (за ~единицы нс), и пропускать импульсные токи высокой амплитудой (не менее 10 кА). В настоящее время единственными устройствами, отвечающими всем этим требованиям, являются искровые газовые разрядники высокого давления.

Статический пробой в газе

Кратко рассмотрим, что означает «высокое давление» по отношению к разрядникам, используемым в мощной импульсной технике.

Из курса физики газового разряда известно, что статический пробой газового промежутка длиной d происходит при напряжении

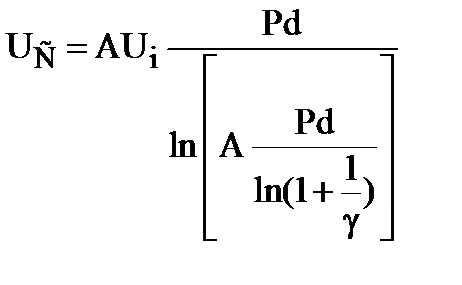, (6)

где 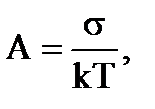s - сечение упругих столкновений электрона с молекулами (или атомами) газа, k – постоянная Больцмана, Т – температура газа в Кельвинах, Ui – потенциал ионизации молекул (или атомов) газа, Р – давление газа, g – коэффициент вторичной эмиссии электронов с катода. Соотношение (6) представляет собой «закон подобия», т.к. напряжение UC зависит только от произведения независимых переменных Р и d.

Уравенение (6) описывает кривую с минимумом, которая называется «кривая Пашена».

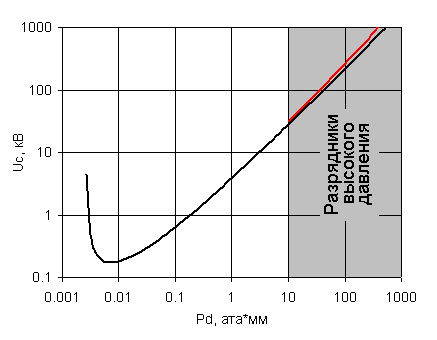
Рис. 3. Кривая Пашена (черным) и соотношение (7) (красным) для сухого воздуха.

Значения (Pd)КР, при которых кривая Пашена имеет минимум, и соответствующие минимальные значения пробивного напряжения 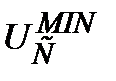для некоторых газов приведены в таблице:

Газ	(Pd)КР, 10-3ата*см	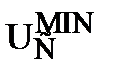, В
Воздух	0,75
Аргон	1,18
Кислород	0,92
Гелий	5,26

Искровые газовые разрядники высокого давления – это разрядники, работающие на правой ветви кривой Пашена при Pd ≥ 1 ата*см >> (Pd)КР. Правая ветвь кривой Пашена при таких давлениях аппроксимируется уравнением (для воздуха)

Uc[kV]≈24.5Pd+6.7*(Pd)^0.5 (7)

см. красную кривую на рис. 3. Подчеркнем, что в (7) давление Р измеряется не в относительных, а в абсолютных атмосферах (ата).

Кривая Пашена (и соотношение (7)) справедливы для однородного распределения электрического поля в промежутке d. На практике поле в промежутке редко бывает однородным, поэтому соотношение (7) следует рассматривать лишь как общую тенденцию. Неоднородность поля уменьшает пробивное напряжение, что можно учесть некоторым геометрическим фактором, превышающим единицу, на который следует поделить правую часть (7). Важно, однако, что и в этом случае выполняется закон подобия, так что напряжение пробоя в газе при любой геометрии электродов при Pd >> (Pd)КР определяется произведением длины промежутка d на давление газа P.

Импульсный пробой в газе

Критерий (7) дает необходимое условие для статического пробоя газового промежутка, но не поясняет, как этот пробой развивается во времени. Из физики газового разряда известно, что для пробоя газового промежутка необходимо, чтобы в электрическом поле на длине свободного пробега электрон приобрел энергию свыше энергии ударной ионизации атомов (или молекул) данного газа. После возникновения ударной ионизации процесс приобретает лавинообразный характер, когда при каждом акте ионизации число свободных электронов удваивается. Такие электронные лавины возникают по всему промежутку, и затем возникает т.н. стример – узкий канал, заполненный слабо-ионизованной плазмой, пронизывающий весь промежуток от катода до анода. Далее основной ток разряда переключается в тело этого стримера, оно нагревается, расширяется, его сопротивление в конечном итоге падает, что и означает «пробой» газового промежутка. Для статического пробоя все эти процессы не представляют интереса, однако приобретают решающее значение для работы искровых разрядников в импульсных генераторах.

Если время воздействия напряжения на промежуток уменьшается до менее, чем ~ 1 мкс, то пробивное напряжение этого промежутка увеличивается по сравнению с (7). В этом случае говорят об «импульсном пробое» газа. Увеличение импульсного пробивного напряжения по сравнению со статическим (7) происходит потому, что электрический пробой является, вообще говоря, вероятностным процессом, при котором нельзя в точности предсказать, при каком напряжении (или напряженности поля) произойдет пробой в тех или иных условиях, а можно вычислить только вероятность этого события. Для импульсного пробоя газа необходимо (см. рис. 4), во-первых, чтобы напряжение превысило статическое пробивное напряжение UC (на это уходит время t0), во-вторых, чтобы в промежутке появились свободные электроны и образовался стример (на это уходит время tЗ), в-третьих, чтобы из этого стримера сформировался низкоомный искровой канал, закорачивающий межэлектродный промежуток (на это уходит время tK – время коммутации).

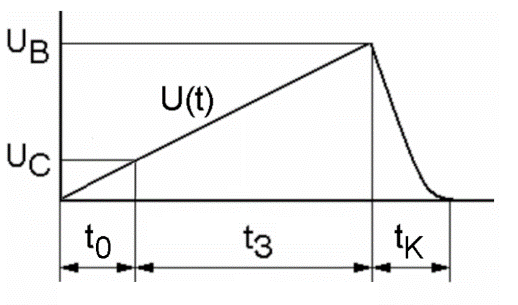
Рис. 4. Временные интервалы различных стадий при развитии импульсного пробоя в газе.

Вероятность образования стримера отлична от нуля только при U(t)>UC, где UС – статическое напряжение самопробоя, определяемое соотношением (7). Эта вероятность должна падать с уменьшением времени наблюдения tЗ, но расти с повышением напряжения на промежутке U(t). Поэтому можно ожидать, что вероятность импульсного пробоя должна оставаться примерно постоянной при постоянной величине произведения U(t)tЗ.

Длительность (t0 + tЗ) в значительной степени определяется характеристиками импульса напряжения U(t), в то время как время коммутации tK определяется свойствами самого разрядника. «Идеальный» разрядник – это такой, у которого сопротивление падает от бесконечности до нуля за время tK = 0. У реального разрядника сопротивление падает (не от бесконечности и не до нуля) за вполне определенное время tK, которое зависит в том числе от конструкции разрядника.

Сопротивление искрового канала

После того, как стример пересек межэлектродный промежуток, образовавшийся искровой канал (или просто «искра») имеет некоторую малую, но конечную проводимость, так что протекание тока по этому каналу приводит к выделению в нем тепловой энергии. Эта энергия расходуется на нагрев плазмы в искре, возбуждение остаточного газа, излучение и т.д. Существующие теоретические модели искры (Ромпе-Вейцеля, Теплера, Брагинского) в разной степени учитывают эти процессы и поэтому по-разному описывают эволюцию сопротивления искры во времени. Тем не менее, все они дают зависимость сопротивления искры в виде

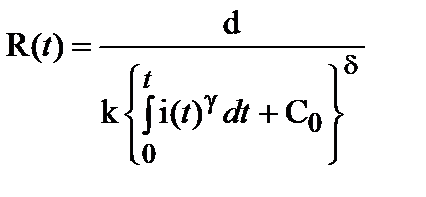, (8)

где d – длина газового промежутка, С0 – параметр, определяемый сопротивлением искры в начальный момент времени t = 0, за который принят момент перемыкания стримером межэлектродного зазора; k, g и d - параметры, определяемые моделью искры.

Из (8) следует, что скорость падения сопротивления R(t) определяется скоростью нарастания интеграла .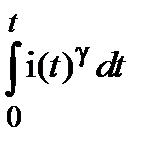

Время коммутации искрового промежутка

По искровому промежутку с сопротивлением R(t) протекает ток i(t), и поэтому на нем выделяется напряжение R(t)i(t), которое падает с течением времени t. Время падения этого напряжения определяет время коммутации tK, и поэтому время tK определяется падением сопротивления R(t). Для определения этой зависимости рассмотрим схему на рис. 3, в которой источник постоянного напряжения с амплитудой UB в момент t = 0 включается идеальным разрядником на активную нагрузку RН через переменное сопротивление R(t), имитирующее искровой промежуток. Будем считать, что величина сопротивления R(t) определяется соотношением (7).

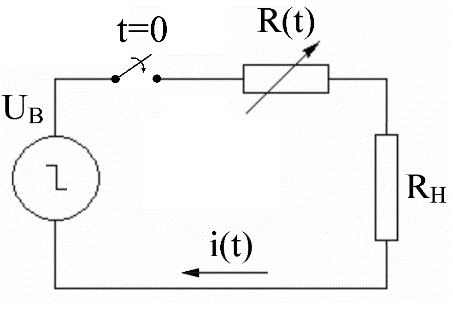
Рис. 5. Источник постоянного напряжения U_В, включенный на нагрузку R_H через газовый промежуток, сопротивление которого R(t) меняется во времени согласно (8).

Уравнение цепи этой схемы при t > 0 имеет вид

.

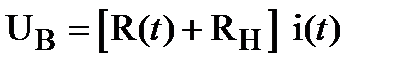Отсчет времени t = 0 ведется с момента перемыкания стримером искрового промежутка, когда его сопротивление R(0) еще очень велико, так что при любом конечном R_H выполняется: R(0) >> R_H. Тогда при 0 £ t £ t_K, где t_K – характерное время, за которое сопротивление R(t) падает от R(0) >> R_H до R(t_K) ~ RH, в уравнении цепи можно пренебречь сопротивлением R_H по сравнению с R(t).

В импульсной технике используются два типа искровых газовых разрядников – неуправляемые и управляемые. Неуправляемые разрядники – это разрядники, в которых пробой инициируется и развивается под воздействием самого напряжения U_B, которое нарастает до величины U_B > UC, где U_C – статическое пробивное напряжение, определяемое законом подобия (4). Положив U_B = U_C + DU, запишем t_K в виде

t_K = 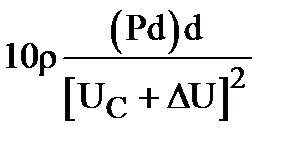. (9)

Из (9) следует, что в неуправляемых разрядниках:

(1) – время tK падает при уменьшении длины зазора d и пропорциональном увеличении давления P. При этом произведение (Pd) не меняется, поэтому U_C и вместе с ним рабочее напряжение разрядника сохраняются, и уменьшается только время коммутации – разрядник начинает срабатывать быстрее.

(2) – время tK падает с ростом перенапряжения DU при прочих равных условиях. Но из уронения 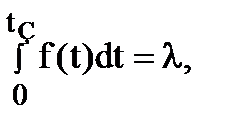(10)

(10)

где

,

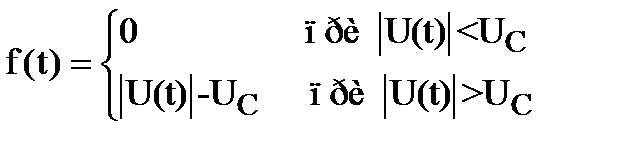следует, что необходимое для пробоя разрядника перенапряжение DU растет с ростом скорости нарастания рабочего напряжения. Следовательно, время коммутации неуправляемых разрядников падает с ростом скорости нарастания рабочего напряжения (см. рис.6).

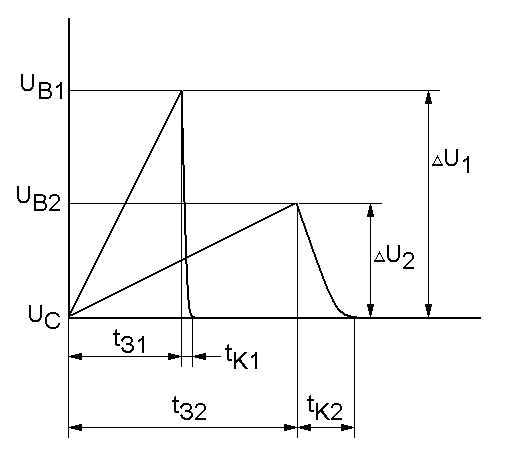
Рис. 6. Поскольку t_З1 < t_З2, t_З1´DU₁ = t_З2´DU₂ ~ l, то DU₁ > DU₂ и из (9) следует: t_К1 < t_К2.

Управляемые разрядники – это разрядники, которые не пробиваются под воздействием рабочего напряжения U_B, для инициирования пробоя управляемых разрядников требуется внешний пусковой импульс. Этот пусковой импульс может быть электрическим или, например, лазерным, его задача состоит в том, чтобы создать начальный стример, в теле которого развивается пробой искрового промежутка под действием рабочего импульса напряжения U_B. В управляемых разрядниках U_B < U, так что к управляемым разрядникам применим только вывод (1).