Уравнение Ван-дер-Ваальса

Уравнение Клапейрона-Менделеева описывает идеальные газы. Ван-дер-Ваальс предложил в этом уравнении учесть собственный объем молекул и силы межмолекулярного взаимодействия:

1.Наличие сил отталкивания между молекулами приводит к тому, что фактический объем, в котором могут двигаться молекулы, равен V_m - b, где V_m - молярный объем, b - объем, занятый самими молекулами.

2.Наличие сил притяжения между молекулами приводит к появлению дополнительного давления на газ p`=a/V_m², где а - постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного взаимодействия.

Введя эти поправки в уравнение Клапейрона-Менделеева, получим уравнение Ван-дер-Ваальса для 1 моля газа

(p + a/V_m²)(V_m - b) = RT или для произвольного количества вещества (p + n²a/V²)(V/n - b) = RT, где поправки a и b - постоянные для каждого газа величины, определяемые из эксперимента (записываются уравнения Ван-дер-Ваальса для двух состояний [p₁, V₁ и p₂, V₂] и решаются относительно a и b).

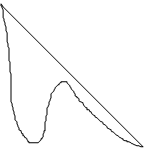
Экспериментальные изотермы реального газа (СO₂) (т.е. зависимости p от V_m при фиксированной Т) для различных температур приведены на рис.2. Для удобства V_m заменена на V. При высоких температурах T > T_к изотермы реального газа мало отличаются от изотермы идеального газа. При некоторой температуре Т_к появляется точка перегиба. Эта изотерма называется критической, а соответствующие ей температура Т_к, объем V_к и давление p_к, - называются критическими. Состояние с критическими параметрами называется критическим состоянием. При более низких температурах все изотермы имеют горизонтальный участок, причем разность V₂ - V₆ молярных объемов горизонтальных участков возрастает с понижением температуры. Все докритические изотермы (Т < Т_к) описывают переход вещества из газообразного состояния в жидкое (рис.3): участок 1®2 соответствует газообразному состоянию (вещество в газообразном состоянии при Т<Т_к называется паром), участок 2®6 соответствует переходу веществ из газообразного в жидкое состояние и участок 6®7 соответствует жидкому состоянию (участок 6®7 почти вертикален вследствие малой сжимаемости жидкости). Пар, находящийся в равновесии со своей жидкостью, называется насыщенным. Точка 6 соответствует состоянию кипящей жидкости, точка 2 - соответствует состоянию сухого насыщенного пара, а любая точка на участке 2-6 соответствует состоянию влажного пара (влажный пар является двухфазной системой, состоящей из кипящей жидкости и сухого насыщенного пара ).

Рассмотрим теперь теоретические изотермы Ван-дер-Ваальса, т.е. кривые зависимости p от V_m при фиксированных Т (для удобства V_m заменена на V). На рис.4 кривая приведена для Т < Т_к (при Т > Т_к эти кривые схожи с экспериментальными на рис.2). Для экспериментальных изотерм при Т < Т_к наблюдается горизонтальный участок (рис.2), а для теоретических - волнообразный (рис.4). Для объяснения этого различия следует иметь в виду, что уравнение Ван-дер-Ваальса является уравнением третьей степени относительно V (при заданных р и Т) и, следовательно, оно может иметь либо три вещественных корня, либо два мнимых и один вещественный корни. Физический смысл имеют только вещественные корни. Поэтому первый случай соответствует изотермам при низких температурах (три вещественных корня), а второй - изотермам при высоких температурах (один вещественный корень). Изотерма при Т < Т_к на участках 1®2®3 и 5®6®7 при уменьшении объема V показывает возрастание давления р, что естественно. Однако на участке 3®4®5 уменьшение объема (сжатие вещества) приводит к уменьшению давления - это противоречит эксперименту. Наличие участка 3®4®5 означает, что при постепенном изменении объема вещество не может оставаться в виде однородной среды и в в действительности происходит распад вещества на две фазы. Таким образом, истинная (экспериментальная) изотерма будет иметь вид ломаной линии 1®2®6®7. При некоторых условиях могут быть реализованы состояния, изображаемые участками 2®3 и 5®6 - эти неустойчивые состояния называются метастабильными и называются перегретой жидкостью (участок 5®6) и пересыщенным паром (участок 2®3).

T₁

p T_к Т₃ p 7 p

7

Т₂

p_к 3

6 2 6 2

V 1 5 1

V₆ V_к V₂ V V

Рис.2. Рис.3. Рис.4.