Если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности

Индукцию 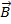проводника с током можно представить как векторную сумму элементарных индукций 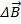создаваемых отдельными участками проводника. На опыте можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад 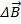в магнитную индукцию 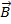результирующего магнитного поля, создаваемый малым участком Δl проводника с током I.

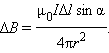
Здесь r – расстояние от данного участка Δl до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ₀ – магнитная постоянная. Направление вектора 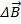определяется правилом буравчика: оно совпадает с направлением вращения рукоятки буравчика при его поступательном перемещении вдоль тока. Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, то получится формула для магнитной индукции поля прямого тока:

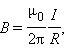
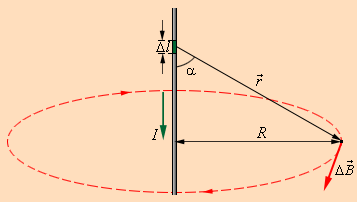Иллюстрация закона Био–Савара на примере магнитного поля прямолинейного проводника с током..

Закон Био–Савара позволяет рассчитывать магнитные поля токов различных конфигураций. Например, магнитное поле в центре кругового витка с током. Этот расчет приводит к формуле

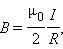
где R – радиус кругового проводника.

Для определения направления вектора 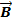используют правило буравчика, вращая его рукоятку в направлении кругового тока, а поступательное перемещение буравчика укажет направление вектора магнитной индукции.

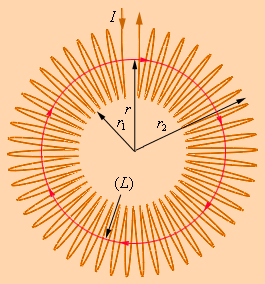
магнитное поле тороидальной катушки

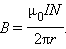
где N – полное число витков, а I – ток, текущий по виткам катушки. Следовательно,

Таким образом, модуль вектора магнитной индукции в тороидальной катушке зависит от радиуса r. Если сердечник катушки тонкий, то есть r₂ – r₁ << r, то магнитное поле внутри катушки практически однородно. Величина n = N / 2πr представляет собой число витков на единицу длины катушки. В этом случае B = μ₀In.

В это выражение не входит радиус тора, поэтому оно справедливо и в предельном случае r → ∞. Но в пределе каждую часть тороидальной катушки можно рассматривать как длинную прямолинейную катушку. Такие катушки называют соленоидами.

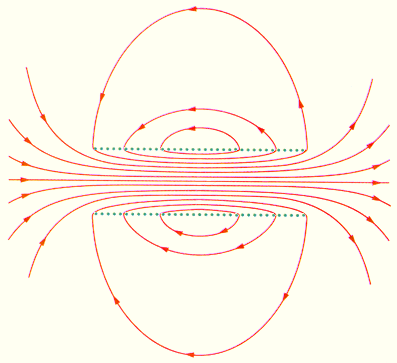На рис. изображено магнитное поле катушки конечной длины. Следует обратить внимание на то, что в центральной части катушки магнитное поле практически однородно и значительно сильнее, чем вне катушки. На это указывает густота линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле целиком сосредоточено внутри соленоида.

В случае бесконечно длинного соленоида выражение для модуля магнитной индукции можно определить по формуле B = μ₀In.

Если поле создается несколькими источниками, то вектор магнитной индукции в данной точке определяется по принципу суперпозиции:

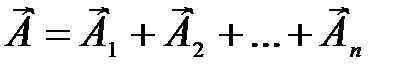
т.е. результирующая магнитная индукция 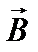– это векторная сумма векторов магнитной индукции, создаваемых каждым источником в отдельности.

Магнитное поле характеризуют не только индукциейВ, но и напряженностьюН магнитного поля. Эти две физические величины связаны между собой: 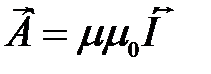. Тогда закон Био-Савара-Лапласа можно представить в виде: .

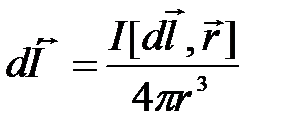Сила Лоренца

Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B, F = IBΔl sin α может быть выражена через силы, действующие на отдельные носители заряда.

Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение nqυS, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику: I = qnυS.

Выражение для силы Ампера можно записать в виде: F = qnSΔlυBsin α.

Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно nSΔl, то сила, действующая на одну заряженную частицу, равна F_Л = qυBsin α.

Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью 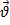и вектором магнитной индукции 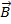Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика.

При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется.

Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость 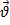лежит в плоскости,

перпендикулярной вектору 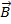то частица будет двигаться по окружности радиуса R. Радиус Rможно определить из равенства центростремительной силы и силы Лоренца: 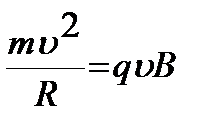,откуда .

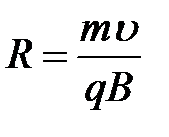Сила Лоренца в этом случае играет роль центростремительной силы.

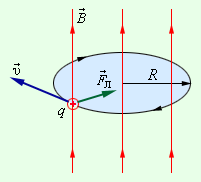
Попадание летящей частицы в магнитное поле вызывает изменение ее траектории в зависимости от знака частицы.

Если частица движется под углом b к линиямВ, то траектория движения частицы будет винтовой линией (спиралью).

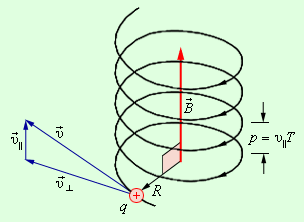Период обращения частицы в однородном магнитном поле равен

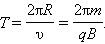
Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории R.

Угловая скорость движения заряженной частицы по круговой траектории

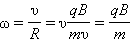
называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов).

Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное электрическое напряжение, частота которого равна циклотронной частоте. Заряженные частицы инжектируются в центре вакуумной камеры. Частицы ускоряются электрическим полем в промежутке между дуантами. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.