Классическая теория дисперсии

ВЗАИМОДЕЙСТВИЕ СВЕТА С ВЕЩЕСТВОМ

Дисперсия света

Дисперсия света - это явления, обусловленные зависимостью показателя преломления вещества от длины волны (или частоты):

n = f (l), где l - длина волны света в вакууме.

Производную dn/dl называют дисперсией вещества.

Для прозрачных бесцветных веществ график зависимости n(l) в видимой части спектра имеет вид, показанный на рисунке. Интервал длин волн, в котором dn/dl < 0 (как на рисунке), соответствует нормальной дисперсии. Те же интервалы длин волн, где дисперсия вещества dn/dl > 0, соответствуют аномальной дисперсии. На рисунке показан график зависимости n(l) с участками нормальной и аномальной дисперсии. Заметим, что область аномальной дисперсии совпадает с полосой поглощения c(l).

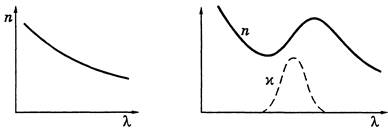
Все вещества в той или иной степени являются диспергирующими. Вакуум, как показали тщательные исследования, дисперсией не обладает.

Аналитический вид зависимости n(l) в области нормальной дисперсии для не слишком больших интервалов длин волн может быть представлен приближенной формулой

n = a + b/l², где а и b положительные постоянные, значения которых для каждого вещества определяются из опыта.

Классическая теория дисперсии

Дисперсию света можно объяснить на основе электромагнитной теории и электронной теории вещества. Строго говоря, поведение электронов в атомах подчиняется законам квантовой физики. Однако для качественного понимания дисперсии света достаточно ограничиться классическими представлениями, которые, как это не удивительно, приводят к тем же результатам, что и квантовая теория.

Поставим перед собой задачу объяснить ход зависимости n(w). Известно, что в изотропной немагнитной среде . В свою очередь e можно найти из соотношения e = 1 + c, где c - диэлектрическая восприимчивость, которая является коэффициентом в соотношении Р = ce₀Е, Р - поляризованность, т.е. дипольный момент единицы объема. таким образом:

, где Р_х - проекция вектора Р на ось х, вдоль которой совершаются колебания вектора Е.

Известно, что Р_х = n₀p_x, где n₀ - концентрация диполей, p_x - проекция дипольного момента отдельного диполя. В дальнейшем мы будем рассматривать простейшую модель вещества, состоящего из не взаимодействующих друг с другом атомов. Каждый атом представляет собой ядро, окруженное быстро движущимися электронами, которые в совокупности как бы «размазаны» по сферически симметричной области вокруг ядра. Поэтому принято говорить, что ядро с зарядом q окружено «электронным облаком» с зарядом (- q).

В отсутствие внешнего поля Е центр электронного облака совпадает с ядром, и дипольный момент атома равен нулю. При наличии же внешнего поля Е электронное облако смещается относительно практически неподвижного ядра, и возникает дипольный момент р = ql, где q > 0, а l - вектор, проведенный из центра «облака» к ядру. Проекция вектора р на ось х равна

р_х = ql_x = q(-x) = -qx

здесь х - смещение центра «облака» из положения равновесия, т.е. относительно ядра. Заметим, что центр «облака» ведет себя как точечный заряд (-q).

С учетом последнего соотношения получаем

Как видно, задача сводится к определению х(t) под действием Е_х(t).

Для этого запишем уравнение движения электронного облака как

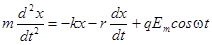, где m - масса электронного облака, а справа записаны проекции на ось х квазиупругой силы, силы «сопротивления», обусловленной чем-то вроде «трения» облака о ядро, и вынуждающей силы со стороны гармонической электромагнитной волны частоты w.

Разделив уравнение на m, приведем его к виду

, где w² = k/m, 2b = r/m, f_m = qE_m/m.

Для теории дисперсии имеет значение не общее, а только частное (установившееся) решение уравнения

x = a cos(wt - j), где а - амплитуда колебаний, j - разность фаз между смещением х и силой f_mcoswt. Подстановка этого решения в дифференциальное уравнение позволяет с помощью векторной диаграммы найти значения амплитуды а и разности фаз j, а именно:

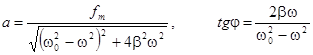(решение уравнения подробно рассматривается в теории колебаний)

Ограничимся простейшим случаем, когда 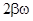<< 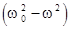, т.е. когда вынуждающая частота (поля) не очень близка к собственной частоте w₀ колебаний электронного облака и коэффициент b, характеризующий затухание, достаточно мал. В этом случае, если w < w₀, то

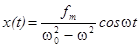
Такой же результат будет и при w > w₀, когда j = p.

Учитывая также, что qE_mcoswt = -qE_x

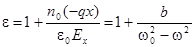, где b = n₀q²/e₀m = N₀e²/e₀m_e, N₀ - концентрация электронов (здесь учтено, что q = Ze, m = Zm_e и N₀ = Zn₀, Z - число электронов в атоме).

Разрыв функции e(w) при w = w₀ и обращение ее в ±¥ не имеют физического смысла, это получилось вследствие игнорирования затухания (b ® 0). Если же его учесть, то ход кривой будет иным (рисунок) и достаточно хорошо подтверждается экспериментально. Зависимость c(w) характеризует полосу поглощения. Как раз с ней совпадает область аномальной дисперсии (dn/dw < 0).

Заметим, что собственных частот w_0i может быть несколько в атоме, соответственно будет и несколько областей аномальной дисперсии. Кроме того, как видно из рисунка, при w > w₀ показатель преломления (n = 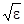) , будет меньше единицы, а это значит, что фазовая скорость электромагнитной волны v = c/n оказывается больше с! Подобное имеет место в плазме, где w₀ = 0 (электроны свободные), и для рентгеновского излучения (w > w₀). Никакого противоречия с теорией относительности здесь нет. Последняя утверждает, что скорость сигнала (импульса) не может превышать с. Понятие же показателя преломления применимо к монохроматическим электромагнитным волнам, бесконечным в пространстве и во времени. Такие волны не могут служить для передачи сигнала, а, кроме того, их в принципе невозможно осуществить.

Из выражения 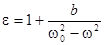вытекает и еще одно неожиданное следствие для случая, когда w₀ = 0 (например, в той же плазме). При этом условии, когда частота электромагнитной волны w , оказывается, что диэлектрическая проницаемость e(w)£ 0, а следовательно, показатель преломления для таких частот становится мнимым, и его можно представить как n = ic. Выясним, что это означает.

Запишем уравнение электромагнитной волны в комплексной форме:

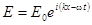, где k = 2p/l, где l - длина волны в среде. Если длина волны в вакууме l₀, то l = l₀/n, и

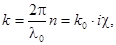
где k₀ = 2p/l₀ и n = ic

Подставив выражение для k в исходное уравнение волны, получим:

E = E₀ exp(-ck₀x)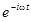

или для действительной части

E = E₀ exp(-ck₀x) coswt

Видно, что в рассматриваемом случае мы имеем стоячую волну, амплитуда которой экспоненциально затухает. Фактически это означает, что излучение при e £ 0 не может пройти через плазму и происходит его полное отражение его в пограничном слое.

Групповая скорость

Волновой пакет

Строго монохроматическая волна это идеализация. Любая реальная волна, согласно теореме Фурье, может быть представлена как суперпозиция монохроматических волн с различными амплитудами и частотами w в некотором интервале Dw. Суперпозицию волн, мало отличающихся друг от друга по частотам (Dw << w), называют волновым пакетом или группой волн. Вид волнового пакета в некоторый момент времени показан на рисунке. В его пределах монохроматические составляющие усиливают друг друга, вне пакета практически гасят друг друга.

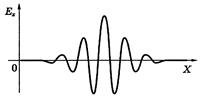
В вакууме все монохроматические волны, образующие пакет, распространяются с одинаковой фазовой скоростью

v = w/k, где k - волновое число (2p/l). С такой же скоростью распространяется в вакууме и сам волновой пакет, не изменяя своей формы.

Групповая скорость

В диспергирующей среде волновой пакет расплывается, поскольку скорости его монохроматических составляющих отличаются друг от друга, и понятие скорости такой волны требует уточнения.

Если дисперсия достаточно мала, расплывание волнового пакета происходит не слишком быстро. В этом случае волновому пакету можно приписать скорость u, с которой перемещается его «центр тяжести». Это так называемая групповая скорость. Соответствующий расчет дает, что групповая скорость определяется как

u = dw/dk

Поясним эту формулу на примере суперпозиции двух волн с одинаковой амплитудой и несколько отличными друг от друга длинами волн (и частотами). На рисунке показано их относительное расположение (а) в некоторый момент времени, а также результат их суперпозиции (б). Нас будет интересовать скорость, с которой перемещается место с максимальной амплитудой - это и будет скорость волнового пакета - групповая скорость. Определим ее величину.

Пусть уравнения этих двух монохроматических волн имеют вид:

E₁ = A cos(wt - kx),

E₂ = A cos[(w + dw)t - (k + dk)x]

В результате их наложения образуется суммарная волна

E = E₁ + E₂ =2A cos 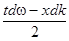cos (wt - kx)

Это выражение можно рассматривать как уравнение монохроматической волны, амплитуда которой меняется по закону

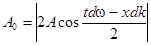
Отсюда следует, что точки, соответствующие, например, максимуму амплитуды, движутся по закону

tdw - xdk = 0, откуда х = (dw/dk)t

Величина в скобках и есть групповая скорость.

Выражение для групповой скорости можно представить в ином виде. Заменив w через vk, получим:

Так как k = 2p/l dk = - (2p/l²)dl, где l - длина волны в среде, то выражение для u можно переписать так:

Это так называемая формула Рэлея. В области нормальной дисперсии (dv/dl > 0) групповая скорость совпадает с фазовой.

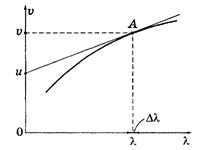
Существует простой графический способ нахождения групповой скорости по кривой v(l). Он показан на рисунке. В случае группы волн роль играет только малый участок кривой v(l) в узком диапазоне Dl (Dl << l). отрезок, который отсекает на оси ординат касательная к кривой v(l), проведенная через точку А, равен v - l (dv/dl), т.е. групповой скорости u при данной длине волны l.

Следует отметить, что в области аномальной дисперсии импульс сильно деформируется, и групповая скорость в таких условиях теряет определенное физическое содержание.