Макро- и микросостояние. Термодинамическая вероятность (статистический вес) данного макросостояния

Первое начало термодинамики указывает на возможность теплового процесса.

Второе начало термодинамики указывает на направление теплового процесса.

Различные формулировки второго начала термодинамики:

1) Все реальные самопроизвольные процессы идут в таком направлении, что теплота передается от более горячего тела к более холодному (формулировка Клаузиуса).

2) Все реальные самопроизвольные процессы идут в таком направлении, что система переходит из менее вероятных в более вероятные состояния.

3) Все реальные самопроизвольные процессы идут в таком направлении, что энтропия системы увеличивается.

4) Невозможно построить такой периодически действующий тепловой двигатель (вечный двигатель второго рода), который работал бы только за счет охлаждения какого-либо тела (формулировка Кельвина).

Рассмотрим термодинамическую систему, которая разделена на пространственные и энергетические ячейки.

Макросостоянием называется состояние термодинамической системы с заданным распределением частиц по ячейкам безотносительно к их номерам.

Пусть в системе имеется N одинаковых частиц и много ячеек.

Одним из макросостоянием системы будет такое, для которого в первой ячейке находится N₁ частиц, во второй – N₂ частиц и т.д.

Если одна частица из первой ячейки, поменялась местом с частицей из любой другой ячейки, то макросостояние системы осталось неизменным.

Если же частица перешла из одной ячейки в другую и количественное распределение частиц по ячейкам изменилось, то макросостояние системы также изменилось.

Каждое макросостояние может быть осуществлено большим числом микрораспределений.

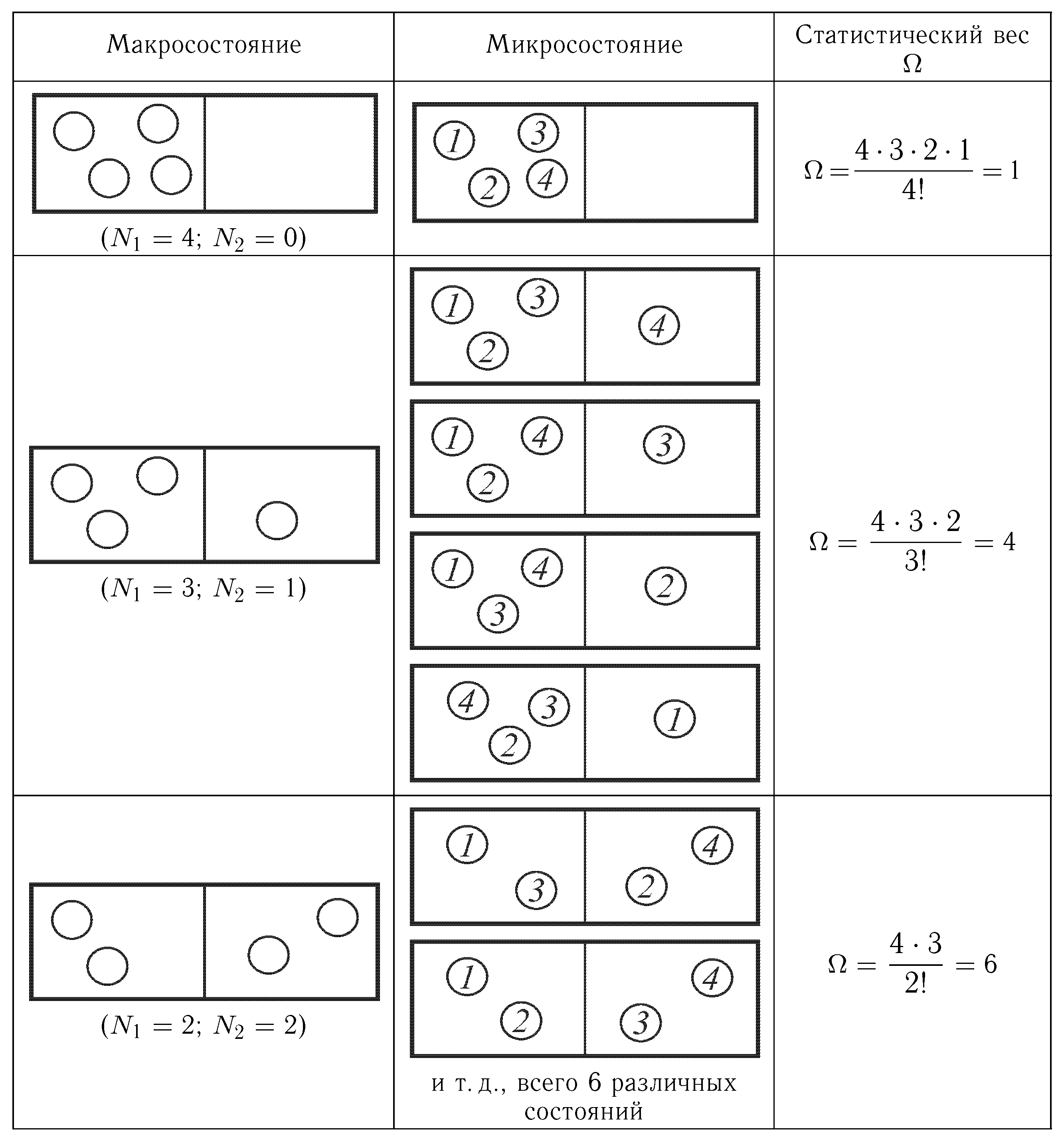
Микросостоянием термодинамической системы это одно из возможных распределений нумерованных частиц по ячейкам системы.

Рассмотрим систему, состоящей из четырех частиц, каждая из которых может находиться в одной из двух ячеек системы.

В данном случае возможно пять различных макросостояний.

Эти макросостояния могут быть реализованы различными способами.

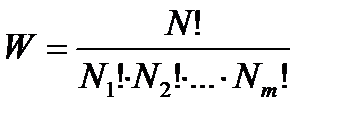Рассчитаем число микросостояний W, с помощью которых может быть осуществлено заданное макросостояние по формуле:

где N – полное число частиц в системе, состоящей из ячеек; N_m – число частиц в m-ой ячейке.

Из формулы видно, что разные микросостояния имеют различную термодинамическую вероятность (статистический вес).

Число микросостояний, посредством которых реализуется данное макросостояние системы, называется термодинамической вероятностью этого макросостояния.

То есть это число микросостояний, которые реализуют данное макросостояние системы.

Максимальная термодинамическая вероятность соответствует равновесному макросостоянию.

В отличие от математической вероятности термодинамическая вероятность W >1. Математическая вероятность P <1.

Найдем термодинамические вероятности макросостояний.

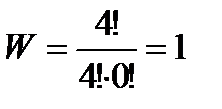1 случай. N=4, N₁=4, N₂=0.

По определению 0!=1.

2 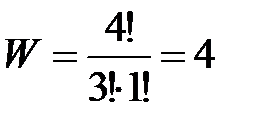случай. N=4, N₁=3, N₂=1.

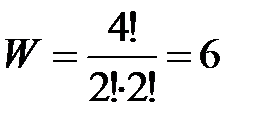3 случай. N=4, N₁=2, N₂=3.

Из полученных данных видно, что даже в случае небольшого числа частиц термодинамическая вероятность макросостояния, при котором распределены по ячейкам равномерно (равновесное состояние) заметно больше термодинамической вероятности макросостояний, при которых частицы распределены неравномерно (неравновесное состояние). Чем больше число частиц в системе, тем больше термодинамическая вероятность равновесного состояния.

Термодинамическая вероятность позволяет предсказать возможное направление изменения состояния системы при самопроизвольных процессах.