Электронная теория дисперсии

Лекция «Взаимодействие электромагнитных волн с веществом»

1.Дисперсия света

2.Электронная теория дисперсии

3.Поглощение света. Закон Бугера

4.Излучение Вавилова- Черенкова

Дисперсия света

Дисперсия – это зависимость показателя преломления среды от частоты или длины волны. Более физично надо сказать, что дисперсия это зависимость фазовой скорости от частоты.

Следствием дисперсии является разложение призмой белого света в спектр. Данное явление впервые обнаружил Ньютон в 1672г. Угол отклонения Д лучей зависит от преломленного угла призмы Р и показатель преломления n. В призме наиболее сильно отклоняются фиолетовые лучи, а наибольшее слабо– красное. Следовательно, угол отклонения зависит от длины волны света.

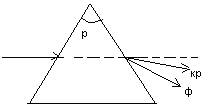D=р(n-1)

n_ф> n_кр

Призма, как и дифракционная решетка, является спектральным прибором, но в дифракционной решетке наиболее сильно отклоняются красные лучи. При помощи дифракционной решетки непосредственно определять длину волны падающего света. Призма же дает лишь зависимость угла отклонения от длины волны. Отношение 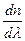называется дисперсией вещества. Она показывает, как быстро изменяется показатель преломления среды с изменением длины волны. Чем больше длина волны, тем меньше n; или чем больше частота, тем больше n.

Д= 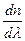(1)

В формуле (1) при уменьшении длины волны увеличивается показатель преломления и соответственно увеличивается дисперсия. Такое поведение дисперсии называется нормальной. Вблизи линий и полос поглощения с уменьшением λ, показатель преломления уменьшается, соответственно уменьшается Д и такая дисперсия называется нормальной.

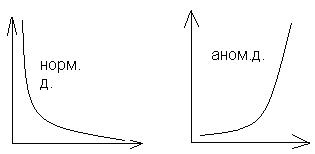
На явлении нормальной дисперсии основана работа спектрометров.

Электронная теория дисперсии

При изучении электромагнитной природы световых волн Максвеллом, им была получена формула, связывающая оптические, магнитные и электрические свойства среды.

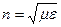(1) - формула Максвелла

Для видимого спектра для всех длин волн магнитная проницаемость µ, µ=1, а это значит, что показатель преломления 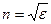, так как ε считается 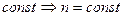. На самом деле n зависит от частоты или λ, то есть электромагнитная теория Максвелла не объясняет явление дисперсии. Трудность объяснения дисперсии с точки зрения теории Максвелла устраняется в электронной теории дисперсии Лоренца. В теории Лоренца дисперсия рассматривается как результат взаимодействия электромагнитной волны с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания под действием переменного электрического поля.

Рассмотрим электронную теорию дисперсии и предположим, что электрическая проницаемость зависит от частоты проницаемости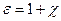

χ- электрическая восприимчивость вещества

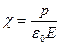
где р - вектор мгновенной поляризации

ε₀- диэлектрическая проницаемость вакуума

Е- напряженность электрического поля

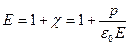(2)

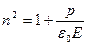(3)

Мы будем рассматривать прозрачный диэлектрик, в котором поляризуются электроны, то есть мы будем рассматривать электронную поляризацию. Электронная поляризация, то есть вынужденные колебания электронов под действием падающей электромагнитной волны будет играть преобладающую роль по сравнению со всеми другими видами поляризации, так как частота падающего света приблизительно 10¹⁵Гц, то это слишком большая частота, чтобы поляризовать атомы в молекулы. В первом приближении можно считать, что вынужденные колебания совершает только самый внешний электрон. Этот электрон наиболее слабо связан с ядром атома и поэтому под действием оптической электромагнитной волны. Он начинает совершать вынужденные колебания. Внешний электрон в атоме называется оптический электрон, приобретает наведенный дипольный момент, который определяется формулой 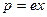(4)

(4)

е- заряд электрона

х – смещение электрона

P=n₀p (5)

Р - вектор мгновенной поляризации и р- наведенный дипольный момент связаны между собой формулой (5); n₀- концентрация атомов в диэлектрике. Тогда формула (3) с учетом формул (4), (5) запишется как

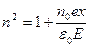(6)

Падающая световая волна описывается выражением E=E₀coswt

E₀- амплитудное значение напряженности электрического поля. Эта световая волна создает внешнюю вынуждающую силу, которая будет периодическим

F=eE=eE₀coswt (7)

Тогда запишем все силы, движущие на электрон и найдем равнодействующую этих сил.

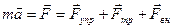(8)

Формула (8) можно переписать в виде:

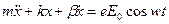
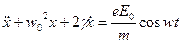(9)

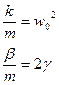
Так как мы рассматриваем прозрачный диэлектрик, то мы предполагаем, что затухание световых волн при прохождении через диэлектрик будет крайне незначительно, а это значит, что γ ≈→0 следовательно уравнение (9) можно записать как:

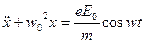(9а)

Решением уравнения (9а) получено нами в классической механике и называется уравнение вынужденного колебания, его решением будет выражение

X=Acoswt (10)

А- амплитуда незатухающего колебания

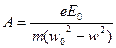(11)

m- масса электрона

w₀- собственная частота внешнего электрона

w- частота падающей электромагнитной волны

Подставим в уравнение (6) формулу (10), (11)

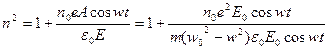
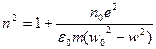(12)

Формула (12) описывает явления электронной дисперсии учитывающей колебания внешнего электрона. Если усложнить рассмотрение, то есть рассмотрим поляризацию не только внешнего электрона, но и всех имеющихся электрических зарядов, то формула, выражающая дисперсию примет вид:

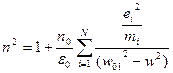(13)

N-число разных электрических зарядов

Формула (13) отражает явление дисперсии в наиболее общем виде. Рассмотрим дисперсию для газов, у которых n≈1. Будем работать с (12)

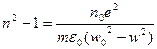
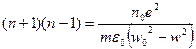
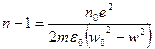
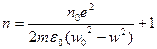(14) - показатель преломления в газах

Проанализируем графически формулу (12), то есть рассмотрим, как изменится показатель преломления от частоты, падающей электромагнитной волны.

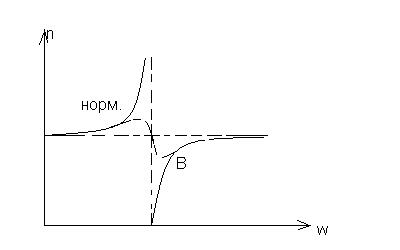Рассмотрим изменение частоты внешней электромагнитной волны от w=0, w= w₀

в формуле (12) 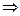n²>1. При росте частоты от 0 до w₀ знаменатель формулы (12) уменьшится, сама дробь увеличится, соответственно увеличится n. Он больше 1, то есть с ростом w до w₀ увеличиться n среды, следовательно, наблюдается нормальная дисперсия. В точке w= w₀ происходит разрыв функции и 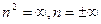. При частоте w> w₀ второе слагаемое в формуле (12) идет со знаком «- » и, следовательно, n² <1. При дальнейшем росте w-n увеличивается по модулю и стремится к единице, то есть с увеличением частоты увеличивается показатель преломления и дисперсия так же нормальная. Но эти рассуждения справедливы лишь при отсутствии затухания, если же учитывать силы сопротивления, то график изобразится в виде пунктирной линии АВ. АВ - это область аномальной дисперсии. Аномальная дисперсия – это когда с ростом частоты показатель преломления уменьшается. Советскому физику Рождественскому принадлежит классическая работа, по изучению показателя преломления для газов и экспериментально показал, что функция связи n с w достаточно хорошо согласуется. Рождественский ввел в формулу (12) поправку, учитывающую квантовые свойства электронов и атомов.