Розподіл Максвела-Больцмана

Лекція 5

РОЗПОДІЛ БОЛЬЦМАНА ТА ЙОГО ЕКСПЕРИМЕНТАЛЬНА ПЕРЕВІРКА. РОЗПОДІЛ МАКСВЕЛА-БОЛЬЦМАНА

1. Розподіл Больцмана.

2. Розподіл Максвела-Больцмана.

3. Експериментальна перевірка закону Больцмана. Досліди Перрена.

4. Броунівський рух. Досліди Перена по визначенню числа Авагадро.

Розподіл Больцмана.

Розподіл Больцмана та його експериментальна перевірка. Розподіл Максвела-Больцмана в його найбільш загальному вигляді.

Література: [1] стор. 79-86, [2] стор. 48-55, [7] стор. 274-290.

• При підйомі частинок в полі сил тяжіння їх кінетична енергія зменшується. Чому при цьому температура в полі сил тяжіння в стані рівноваги не залежить від висоти?
• Яким чином розподіл Больцмана застосовується до суміші газів?
• Як розподіли Максвелу та Боцмана пов’язані між собою?

Броунівський рух

Рух броунівської частинки. Досліди Перена.

Література: [1] стор. 110-115, [2] стор. 42-48, [7] стор. 209-215, 280-284.

· Причини і особливості броунівського руху.

· Розкрийте значимість дослідів Перена для молекулярно-кінетичної теорії.

Розподіл Больцмана

Розподіл Больцмана можна розглядати, як узагальнення барометричного розподілу на випадок довільного потенціального поля 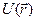(іще кажуть, довільного потенціалу). Справді, не має підстав вважати, що поведінка газу суттєво зміниться, якщо замість сил тяжіння будуть діяти інші сили.

Відповідно, за барометричною формулою

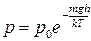, (1)

де 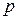- тиск на висоті ,

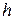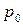- тиск біля поверхні Землі .

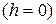Враховуючи, що для ідеального разу

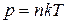, (2)

формула (1) набуває вигляду

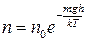. (3)

Як розуміти цю формулу. 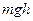- потенціальна енергія молекули на висоті 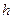в однорідному гравітаційному полі. Тому, якщо газ знаходиться в реальному силовому полі, і його частинки мають певну потенціальну енергію, то кількість часток з потенціальною енергією 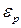визначаються формулою Больцмана

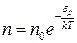. (4)

Відповідно

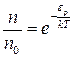- (5)

доля частинок, що в умовах теплової рівноваги мають потенціальну енергію .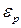

Приклад. Оскільки енергія магнітної частинки з магнітним моментом 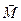дорівнює 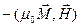, то таких частинок в деякому об’ємі

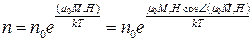
I. З формули (5) видно, що для частинок із певної енергією, залежить лише від температури.

II. При даній температурі доля молекул швидко падає із ростом 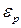. Тобто для молекул з великою енергією завжди мала.

III. Чим нижче температура, тим швидше 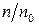спадає із зростанням .

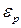Поведінка ідеального газу в певному об’ємі не залежить від наявності інших газів. В стані термодинамічної рівноваги концентрація різних газів в суміші повинні убувати з висотою за різними експонентами, що визначаються молекулярною вагою відповідних компонент (концентрація легких компонент убувають повільніше). В реальній тропосфері не спостерігаються зростання концентрації легких газів із висотою, внаслідок процесів, що призводять до перемішування її нижніх і верхніх шарів.

Розподіл Максвела-Больцмана

У відсутність силових полів концентрація молекули газу всюди однакова. Якщо з’являється силове поле, то концентрація молекул газу від точки до точки змінюється, але (!) швидкості молекул газу в кожній точці простору розподіленні за законом Максвела.

Тоді кількість частинок в об’ємі 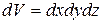визначиться з допомогою формули Больцмана

,

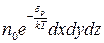а кількість частинок з них, що мають швидкість в межах швидкісного інтервалу 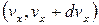, 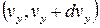та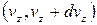

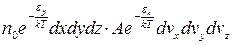
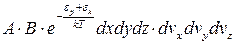
- формула Максвела-Больцмана.

Дане рівняння дає відносну кількість частинок, які, маючи потенціальну енергію 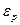, знаходяться в об’ємі 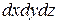біля точки 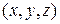і одночасно мають швидкості в швидкісному об’єму 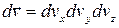поблизу швидкості 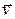. Тобто ця формула визначає відносну кількість частинок в 6-мірному просторі в об’ємі 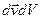біля точки .

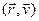I. Закони Максвела та Больцмана пов’язані між собою. Обидва розподіли обумовлені наявністю теплового руху молекул. Тому, використовуючи закон Больцмана, можна отримати закон Максвела (див. Кикоина). І навпаки, маючи розподіл Максвела, можна прийти до розподілу Больцмана (див. Сивухина).

II. Молекули повітря в земній атмосфері рухаються вгору, і їх швидкість зменшується, а ті що рухаються вниз збільшують свої швидкості під дією сил тяжіння. Звідси робимо висновок, середні швидкості молекул нагорі, а з ними і температура повітря повинні бути меншими ніж внизу. Цей парадокс було розв’язано Максвелом.

Коли молекули підіймаються вгору, з їхнього потоку вибиваються найбільш повільні, тобто „холодні” молекули. І розрахунок середньої енергії ведеться за малою кількістю частинок, але за більш „гарячими” з них. При русі вниз, навпаки, частинки прискорюються, але водночас пучок поповнюються більш повільними, „холодними” молекулами. Тобто середня швидкість молекул залишається незмінною. Іще раз, сила тяжіння змінює лише концентрацію частинок, але не температуру.

Лоренц приводив такий приклад: є два міста А і В. Кількість мешканців певного віку в місті А дорівнює подвоєній кількості мешканців того ж віку в місті В. Зрозуміло, що середній вік мешканців міст А і В однаковий.

Дослід Перрена.

Перрен використав той факт, що, невеличкі зважені частинки можна розглядати як невзаємодіючі молекули великих розмірів. Тому можна очікувати, що „макромолекули” зважені у рідині, в полі сил тяжіння будуть розподіленні за висотою як і молекули газу, тобто за законом Больцмана.

Але маси великих частинок великі, і їх концентрація з висотою буде швидко убивати, так що ми отримаємо стан, в якому частинки лежать на дні посудини.

Для того, щоб важкі частинки не „осіли” на дно, а розподілилися у достатньо товстому шарі за висотою, необхідно їх розмістити у рідині, густина якої 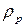лише трохи менша за густину частинок 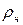. Тоді потенціальна енергія частинок в результаті дії сили Архімеда буде достатньо малою:

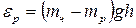. (8)

І розподіл концентрації за висотою буде задаватися формулою:

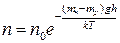. (9)

Складності і особливості досліду див. [7, ст.280-284]