Выражение напряженности поля в виде

Градиента потенциала.

В электростатическом поле между двумя близко расположенными точками в общем случае имеется некоторая разность потенциалов. Если эту разность потенциалов разделить на кратчайшее расстояние между взятыми точками, то полученная величина будет характеризовать скорость изменения потенциала в направлении кратчайшего расстояния между точками. Эта скорость будет зависеть от направления, вдоль которого взяты точки.

В математике используют понятие градиента скалярной функции, под которым понимают скорость изменения скалярной функции, взятую в направлении ее наибольшего возрастания.

Возьмем две близко расположенные эквипотенциальные линии. Одна из них имеет потенциал φ₁, другая – φ₂, причем φ₁ > φ₂ (рис. 38.3). Тогда градиент изобразится вектором, перпендикулярным к эквипотенциальным линиям и направленным от φ₂ к φ₁ (в сторону увеличения потенциала).

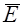Напряженность электрического поля направлена от более высокого потенциала (φ₁) к менее высокому (φ₂). Если через dn обозначить расстояние по нормали между эквипотенциальными поверхностями, а через вектор, совпадающий с направлением напряженности поля , т.е. ( – единичный вектор, направленный по направлению ), то можно записать выражение

где – приращение потенциала при переходе от точки 1 к точке 2.

Так как векторы 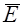и совпадают по направлению, то . Таким образом Отсюда . Вектор напряженности поля . Поэтому

(38.5)

Из определения градиента следует, что

(38.6)

Сопоставляя (19.5) и (19.6), получаем

.

(38.7)

Физический смысл выражения (38.7) заключается в том, что напряженность поля в какой-либо его точке равна скорости изменения потенциала в этой точке, взятой с обратным знаком.

Нормаль в общем случае может не совпадать с направлением какой-либо координатной оси, и поэтому градиент потенциала в общем случае можно представить в виде суммы трех проекций по координатным осям. Например, в декартовой системе координат

(38.8)

Вектор напряженности поля Таким образом,

=

Два вектора равны только тогда, когда равны друг другу их соответствующие проекции. Следовательно

(38.9)

Для сокращения записи в математике используют дифференциальный оператор Гамильтона: используя который можно записать

Вопросы для самоконтроля

1. Какова основная отличительная особенность электромагнитного поля как вида материи?

2. Какими двумя сторонами характеризуется электромагнитное поле? Как эти стороны связаны между собой?

3. Охарактеризуйте понятие «электрическое поле».

4. Какими двумя основными величинами характеризуется электрическое поле?

5. Дайте определение потенциала электрического поля.

6. Какие поля называют потенциальными? Почему суммарная работа по переносу электрического заряда по замкнутому контуру в потенциальном поле равна нулю?

7. Что понимают под силовой линией электрического поля?

8. Какая поверхность в электрическом поле называется эквипотенциальной?

9. В чем смысл знака минус в формуле

10. Могут ли быть замкнутыми силовые линии в электростатическом поле?