И 14.Каноническое и большое каноническое распределения Гиббса в квантовой статистической теории.

1)

Мы рассматриваем макроскопическую систему 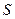, которая находится в равновесии с очень большим термостатом 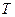. При взаимодействии системы с термостатом число частиц в системе не изменяется.Решаем, как и в классическом случае. Исходим из того, что совокупность нашей системы и термостата (в принятых нами обозначениях система ) является изолированной. Поэтому вероятность ее микросостояний

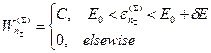. (8)

Здесь энергия 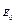задает состояние равновесия всей замкнутой системы

Гамильтониан системы мы пишем как

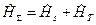. (9)

Уровни энергии 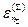системы представляют собой сумму уровней энергии 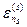нашей системы и уровней энергии 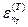термостата

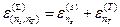. (10)

Тогда условие, определяющее возможные микросостояния нашей системы и термостата запишется как

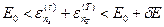, (11)

и для вероятности микросостояний замкнутой системы мы имеем

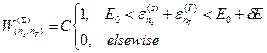. (12)

Нас интересует полная вероятность 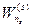микросостояния 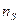нашей системы при всех микросостояниях термостата, возможных в данном состоянии равновесия. Согласно теореме о сложении вероятностей

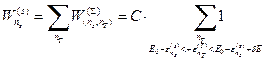. (13)

Рассмотрим величину

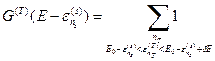. (14)

Эта величина представляет собой число микросостояний, в которых может находиться термостат при заданном микросостоянии нашей системы – число микросостояний термостата, энергия которых попадает в интервал 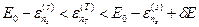. Прежде всего, заметим, что поскольку спектр нашей системы квазинепрерывный, то аргумент функции 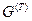меняется практически непрерывно. Кроме того, в силу квазинепрерывности спектра термостата 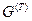есть очень большое число.

Введем в рассмотрение величину

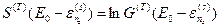. (15)

Логарифм при больших аргументах является очень медленно растущей функцией. Поэтому 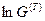очень сильно сгладит особенности функции 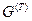, связанные с дискретностью ее значений. Поэтому функция 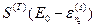может быть с огромной точностью аппроксимирована гладкой функцией, очень хорошей с математической точки зрения. В частности, эту функцию можно раскладывать в ряд.

Чем меньше часть равновесной системы, тем меньшая доля внутренней энергии всей системы приходится на эту часть.

Поскольку наша система есть малая (но макроскопическая) часть системы , то с подавляющей вероятностью реализуются микросостояния нашей системы с энергией 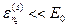, и с большой точностью функцию 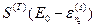можно разложить в ряд Тейлора в окрестности точки 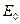, ограничившись только первой степенью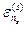

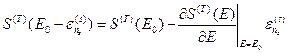. (16)

Следовательно, вероятность микросостояния нашей системы

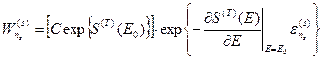. (17)

Величина 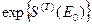не зависит от микросостояния нашей системы и может быть включена в нормировочный множитель, который мы обозначим .

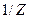Введем независящую от микросостояния величину

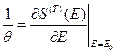. (18)

Тогда вероятность (4.10) запишется в виде

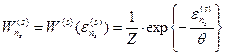. (19)

Величина 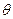есть термодинамическая температура, измеренная в энергетических единицах.

Как легко видеть, нормировочный множитель дается выражением

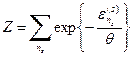. (20)

Нормировочный множитель 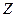называется статистической суммой. Как легко понять, статистическая сумма есть квантовый аналог статистического интеграла (при переходе в классическую механику, статистическая сумма, очевидно, перейдет в статистический интеграл). Поэтому здесь логично ввести в рассмотрение функцию состояния

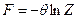, (21)

и попытаться через эту величину выразить внутренние параметры нашей системы – ее внутреннюю энергию, обобщенные силы и энтропию. Мы получаем, что термодинамические обобщенные силы выражаются через функцию состояния как

.

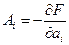Внутренняя энергия выражается через функцию состояния 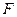как

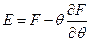. (25)

Перейдем теперь к вычислению энтропии нашей системы. Энтропию нашей системы мы можем определить как

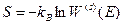. (26)

Следовательно,

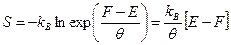. (27)

С учетом (25), находим

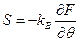. (28)

Таким образом, мы видим, что функция состояния 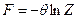является термодинамическим потенциалом – свободной энергией Гельмгольца.

2)В этом случае мы должны рассматривать явную зависимость модельного Гамильтониана системы 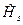от числа частиц 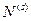в ней. Поэтому когда мы задаем микросостояние нашей системы, мы сначала должны указать число частиц в ней, а затем указать базисный собственный вектор 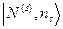гамильтониана 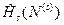нашей системы, когда в ней имеется это число частиц. Аналогично, будет задаваться и состояние термостата.

Соответственно, условия, определяющие микросостояния нашей системы и термостата, примут вид

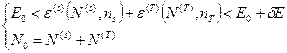. (29)

Здесь 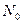- число частиц в изолированной системе .

Полная вероятность микросостояния нашей системы (вероятность того, что в нашей системе 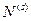частиц и при этом она находится) есть

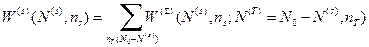. (30)

Здесь

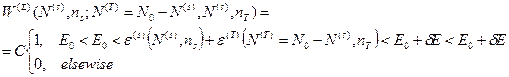(31)

Поскольку число частиц в нашей системе и число частиц в термостате связанны друг с другом соотношением 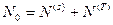, то фиксировав число частиц в нашей системе , мы тем самым фиксируем и число частиц в термостате. Поэтому в формуле (30) суммирование осуществляется по квантовым состояниям термостата в случае, когда он содержит заданное число частиц .

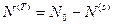Аналогично, предыдущей задачи вероятность микросостояния нашей системы мы можем представить в виде

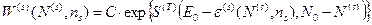, (32)

где

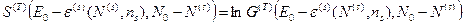, (33)

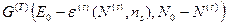- число микросостояний, в которых может находиться термостат при условии, что наша система находится в микросостоянии .

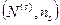Поскольку наша система есть малая часть системы , то с подавляющей вероятностью реализуются микросостояния нашей системы с числом частиц 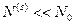и энергией .

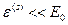Поэтому также как и в предыдущей задаче, функцию 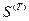мы можем разложить в ряд Тейлора, ограничившись только первой степенью 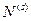и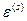

Соответственно, вероятность микросостояния нашей системы принимает вид

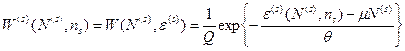(35)

Здесь независящую от микросостояния величину 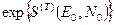мы включили в нормировочный множитель 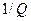, и также ввели независящие от микросостояния величины

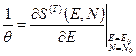(36)

и

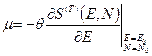(37)

На основании принципа соответствия мы можем утверждать, что 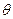- термодинамическая температура и 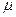- химический потенциал.

Теперь, следуя общей логике, определим через нормировочный множитель функцию состояния системы

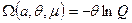, (38)

и, дифференцируя эту функцию по внешним параметрам, температуре и химическому потенциалу, попытаемся выразить через нее внутренние термодинамические характеристики нашей системы – внутреннюю энергию, термодинамические обобщенные силы, среднее число частиц в системе и ее энтропию.

Дифференцируя (38) по химическому потенциалу 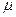, получаем

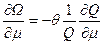, (39)

Из условия нормировки 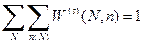, находим нормировочный множитель 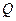(он называется большой статистической суммой)

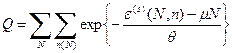(40)

Подставляя в (5.11), находим

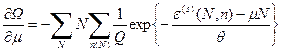, (41)

Таким образом, среднее число частиц выражается через функцию состояния 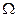как

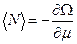. (42)

Дифференцируя (38) по внешнему параметру 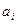, найдем, что термодинамические обобщенные силы выражаются через 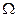как

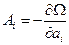. (43)

Дифференцируя (38) по температуре, получим выражение для внутренней энергии

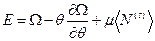. (44)

Рассуждая также как и в предыдущей задаче, получим для энтропии

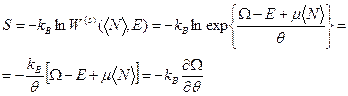. (45)

Таким образом, мы видим, что функция состояния 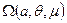представляет собой термодинамический потенциал нашей системы- так называемый большой термодинамический потенциал.