Большое каноническое распределение в классической статистической теории.

При рассмотрении канонического распределения Гиббса предполагалось, что подсистема обменивается с термостатом энергией, а число частиц в ней не изменяется. Однако, чаще всего, подсистема обменивается с термостатом не только энергией, но и частицами. Описанию таких подсистем посвящено большое каноническое распределение Гиббса.

Пусть имеется макроскопическая система, находящаяся в состоянии термодинамического равновесия. Энергия этой системы равна 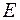и остается величиной постоянной. Число частиц в этой системе равно 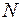и также не изменяется со временем. Выделим в этой системе малую подсистему, энергия которой равна 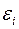, и которая содержит 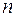частиц. Все остальное окружение подсистемы назовем по-прежнему термостатом. Теперь рассмотрим случай, когда подсистема обменивается с термостатом и энергией и частицами и найдем вероятность того, что подсистема находится в состоянии с энергией 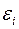и содержит 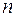частиц.

Пусть число состояний подсистемы равно 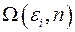, а число состояний термостата 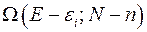. Тогда вероятность того, что подсистема находится в состоянии с энергией 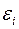и содержит 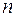частиц, а термостат находится в состоянии с энергией 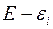и содержит 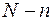частиц, пропорциональна произведению числа состояний, то есть,

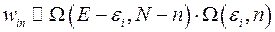(4.1)

Аналогично, для того, чтобы удовлетворялось условие аддитивности для энергий и числа частиц, воспользуемся понятием энтропии: 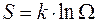и запишем число состояний термостата:

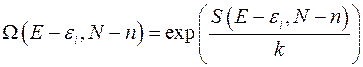(4.2)

Так как 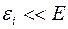и 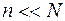, то энтропию 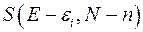можно разложить в ряд по степеням 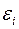и 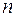. При этом ограничимся только первыми членами разложения. Тогда получаем:

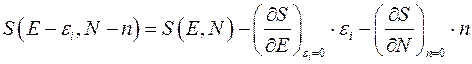(4.3)

Подставляем формулу (4.3) в формулу (4.2) и получаем:

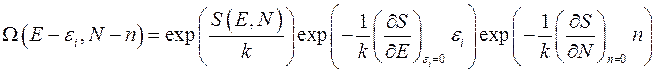(4.4)

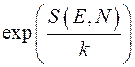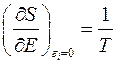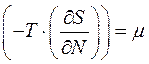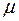В этой формуле величина равна некоторой постоянной, величина , а величина , где - химический потенциал. Тогда 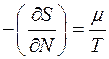(4.5).Теперь формула (4.4) принимает вид:

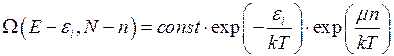(4.6)

Теперь формулу (4.1), описывающую искомую вероятность можно записать в виде:

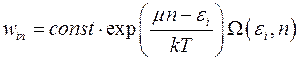(4.7)

Формула (4.7) представляет собой большое каноническое распределение Гиббса. Чтобы найти значение постоянной, воспользуемся условием нормировки, согласно которому имеем:

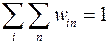(4.8)

Воспользуемся этим условием:

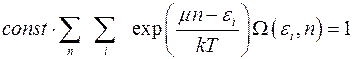(4.9)

Отсюда находим неизвестную постоянную:

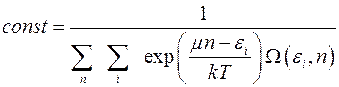(4.10)

Теперь большое каноническое распределение Гиббса можно записать в явном виде:

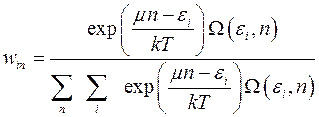(4.11)

По этой формуле можно определить средние значения величин, зависящих от энергии и от числа частиц в подсистеме:

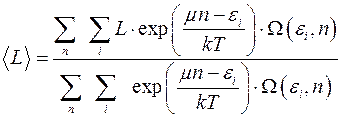(4.12)

Например, можно найти среднее число частиц в подсистеме при произвольном значении ее энергии. Эта величина подробно выведена в формуле (4.13).

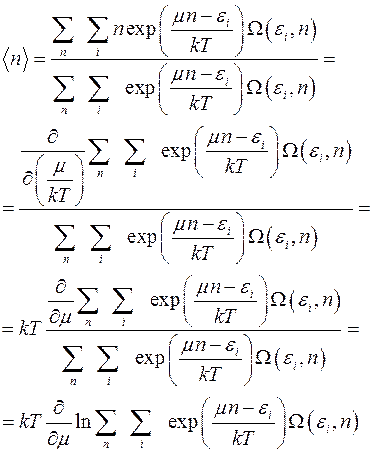(4.13)

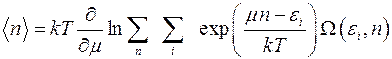(4.13)

Большое каноническое распределение Гиббса, имеющее вид (4.11), можно записать в другом виде:

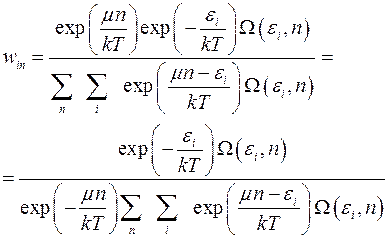(4.14)

Теперь можно ввести обозначение:

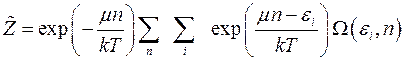(4.15)

Величина 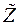называется большой статистической суммой. Это выражение переходит в простую статистическую сумму. Если число частиц в системе постоянно. В этом случае большое каноническое распределение Гиббса переходит в каноническое распределение Гиббса.

Статистическую сумму и большую статистическую сумму называют также функцией состояния или интегралом по состояниям.

Химический потенциал, также как и температура, является характеристикой всей системы. Он показывает, на какую величину изменяется энергия системы частиц при изменении числа частиц на единицу при неизменных других параметрах состояния.

Если в системе содержатся частицы разного сорта. То для каждого сорта частиц вводится свой химический потенциал. Поэтому в общем случае первое начало термодинамики записывается в виде:

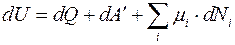, (4.16)

где 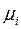- химический потенциал частиц 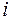- того сорта.

Выражение (4.16) можно записать в виде:

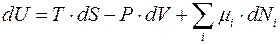(4.17)

Отсюда следует смысл химического потенциала:

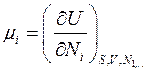(4.18)

Кроме того, отсюда следует использованное выражение для связи энтропии и химического потенциала:

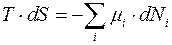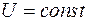при и 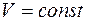. Тогда

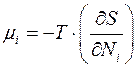(4.19)