Атестація №1 з тем: «Експериментальні і теоретичні основи квантової механіки. Фізичні основи і математичний апарат квантової механіки».
Завдання №1 (0,1 бал за кожне)
1. Який розділ фізики називають квантовою механікою?
а) Фундаментальну фізичну теорію, що вивчає рух та взаємодію макрочастинок в зовнішніх силових полях при швидкостях менших за швидкість світла.
б) Фундаментальну фізичну теорію, що вивчає рух та взаємодію мікрочастинок в зовнішніх силових полях при швидкостях менших за швидкість світла.
в) Фундаментальну фізичну теорію, що вивчає рух та взаємодію мікрочастинок в зовнішніх силових полях за будь-яких швидкостей руху досліджуваних мікрооб’єктів.
2. У чому полягає ідея Планка стосовно пояснення характеру випромінювання у спектрі абсолютно чорного тіла?
а) Оскільки характер випромінювання абсолютно чорного тіла не залежить від його будови, тому пропонується замінити атоми і молекули твердого тіла системою гармонійних осциляторів, що випромінюють і поглинають енергію. Гіпотеза Планка полягає у тому, що рівні енергії осциляторів дискретні.
б) Оскільки характер випромінювання абсолютно чорного тіла не залежить від його будови, тому пропонується замінити атоми і молекули твердого тіла системою гармонійних осциляторів, що випромінюють і поглинають енергію. Гіпотеза Планка полягає у тому, що осциляторів не просто поглинає та випромінює дискретно, а саме випромінювання існує у вигляді окремих дискретних порцій.
в) Оскільки характер випромінювання абсолютно чорного тіла не залежить від його будови, тому пропонується замінити атоми і молекули твердого тіла системою гармонійних осциляторів, що випромінюють і поглинають енергію. Гіпотеза Планка полягає у тому, що випромінювання – це своєрідний набір мікрооб’єктів, що мають подвійний характер, тобто володіють корпускулярно-хвильовим дуалізмом.
3. Сформулювати правило відбору напівкласичної теорії Бора.
а) Випромінювання і поглинання енергії атомами відбувається при його стрибкоподібному переході з одного стаціонарного стану в інший: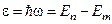 
.
б) Існують стаціонарні стани атома, в яких його енергія не змінюється, а він не випромінює і не поглинає: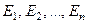 
.
в) Для того, щоб з усіх можливих квантових станів енергії відшукати стаціонарні використовують правило квантування стаціонарних орбіт: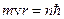 
, 
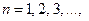
4. Яке значення мають співвідношення неозначеностей Гейзенберга для фізичної теорії?
а) дозволяють пояснити, що хвилі де Бройля – це хвилі імовірності, квадрат модуля яких пов’язаний з імовірністю місцезнаходження частинок.
б) дозволяють пояснити, що точне визначення одночасно координати та відповідної складової імпульсу принципово неможливо.
в) дозволяють узгодити корпускулярні і хвильові властивості мікрочастинок, встановлюють границі застосування до них понять класичної механіки, дають можливість виконувати напівкількісні оцінки явищ мікросвіту.
5. Чи диспергують хвилі де Бройля у вакуумі?
а) хвилі де Бройлер не диспергують у вакуумі, бо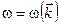 
;
б) хвилі де Бройлер диспергують у вакуумі, бо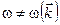 
;
в) хвилі де Бройлер диспергують у вакуумі, бо .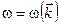
6. Що називають оператором?
а) Оператор – це диференціальна операція, яку необхідно виконати над хвильовою функцією, щоб одержати іншу хвильову функцію.
б) Оператор – це символ для позначення дії чи програми дій, яку необхідно виконати над певною функцією, щоб одержати іншу функцію.
в) Оператор – це математична дія чи група дій, яку необхідно виконати над комплексною функцією, щоб одержати іншу функцію.
7. Що називають хвильовою функцією?
а) Хвильова функція – це математичний образ того хвильового поля, яке пов’язують з кожною мікрочастинкою, залежить від параметрів об’єкта і не залежить від фізичних умов, в яких він перебуває.
б) Хвильова функція – це математичний образ того хвильового поля, яке пов’язують з кожним мікрооб’єктом, що не залежить від параметрів об’єкта і фізичних умов, яких він перебуває.
в) Хвильова функція – це математичний образ того хвильового поля, яке пов’язують з кожним мікрооб’єктом, що залежить від параметрів об’єкта і фізичних умов, в яких він перебуває.
8. Запишіть у загальному вигляді рівняння для власних функцій і власних значень деякого довільного оператора.
а) 
, якщо 
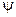–функція задовольняє стандартним умовам та умові нормування 
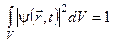, тоді вона є власною функцією оператора 
, а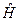 
– його власне значення.
б)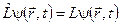 
, якщо 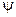–функція задовольняє стандартним умовам та умові нормування 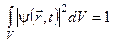, тоді вона є власною функцією оператор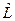а 
, а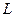 
– його власне значення.
в) 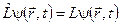, якщо 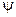–функція задовольняє стандартним умовам та умові нормування 
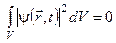, тоді вона є власною функцією оператор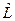а , а 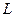– його власне значення.
9. Як визначається імовірність того, що при вимірюванні одержується значення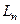 
фізичної величини ?
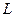а) Імовірність того, що при вимірюванні одержується значення 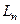фізичної величини 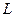, рівна квадрату модуля власних функцій 
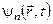оператора цієї величини 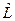, відповідного типу спектрів.
б) Імовірність того, що при вимірюванні одержується значення 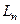фізичної величини 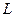, рівна квадрату модуля коефіцієнту 
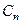розкладу функції 
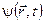за власними функціями 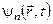оператора цієї величини .
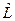в) Імовірність того, що при вимірюванні одержується значення 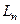фізичної величини 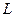, рівна квадрату модуля функції 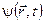за власними значеннями 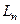оператора цієї величини .
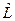10. Сформулювати квантовий принцип причинності.
а) У квантовій механіці існує однозначна динамічна закономірність для хвильової функції, через неї однозначно визначається густина ймовірності місцезнаходження частинки, а не саме місцезнаходження. Однозначно зв’язані не самі стани, а їх потенціальні можливості.
б) У квантовій механіці існує однозначна динамічна закономірність для квадрата модуля хвильової функції, який визначається густину ймовірності місцезнаходження частинки, а не саме місцезнаходження. Однозначно зв’язані не самі стани, а їх статистичні можливості.
в) У квантовій механіці існує неоднозначна динамічна закономірність для хвильової функції, через яку з певною ступінню імовірності визначається місцезнаходження частинки. Однозначно квантові стани між собою не зв’язані, а зв’язані їх потенціальні можливості.
11. Який вигляд має оператор потенціальної енергії?
а)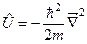 
. б) 
. в)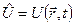 
.
12. Записати квантові співвідношення, які відображають теореми Еренфеста.
а) 
; 
.
б)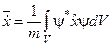 
; 
.
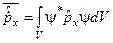в)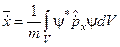 
; 
.
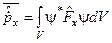13. Як визначається середня густина електричного заряду?
а) 
. б) 
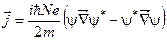. в) 
.
14. Який стан квантової системи називають стаціонарним?
а) Стан квантової системи називають стаціонарним, якщо зовнішнє силове поле в якому вона перебуває не залежить від часу.
б) Стан квантової системи називають стаціонарним, якщо хвильова функція, що описує такий стан не залежить від часу.
в) Стан квантової системи називають стаціонарним, якщо зовнішнє силове поле в якому вона перебуває є залежною від часу.
15. Записати стаціонарне рівняння Шредінгера для координатної частини хвильової функції в диференціальній формі.
а)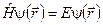 
. б) 
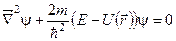. в)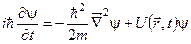 
.
16. Що є предметом дослідження квантової механіки?
а) Всі частинки менші за розмірами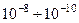 
см та масами 
кг.
б) Всі частинки менші за розмірами 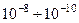м та масами 
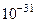кг.
в) Всі частинки менші за розмірами 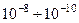м та масами кг.
17. Які фундаментальні експериментальні дослідження показали, що атоми взаємодіючи з електронами, можуть одержувати енергію окремими порціями, що свідчить про дискретність енергетичних станів атомів.
а) Досліди А. Ейнштейна, проведені ним у 1907 р.
б) Досліди Релея-Джинса, проведені ним у 1913 р.
в) Досліди Дж. Франка і Г. Герца, проведені ними у 1914 р.
18. У чому полягає універсальність сталої Планка?
а) Універсальність сталої Планка проявляється в існуванні фундаментального обмеження на величину зовнішнього впливу і вказує на те, що зменшення розмірів області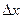 
, де знаходиться мікрооб’єкт автоматично веде до збільшення 
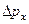, а тому і до збільшення середньої кінетичної енергії, як раз ця обставина протидіє безмежному зменшенню розмірів атома і забезпечує його стійкість.
б) Універсальність сталої Планка проявляється в тому, що через неї можна подати будь-які фізичні характеристики, якими обмінюються два взаємодіючих об’єкта, дійсно розмірність кванта дії може бути різною: [енергія×час], [імпульс×віддаль], [момент імпульсу×момент імпульсу].
в) Універсальність сталої Планка проявляється в існуванні фундаментального обмеження на величину зовнішнього впливу, яке не зв’язано ні з типом самого впливу, ні з природою об’єкта, а з самою природою речей.
19. Які фізичні явища вказують на корпускулярну природу мікрооб’єктів?
а) інтерференція і дифракція; б) фотоефект, ефект Компотна; в) теорія Бора.
20. Як визначається фазова швидкість хвиль де Бройля?
а)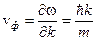 
; б) 
; в)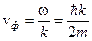 
.
21. Які оператори називають лінійними?
а) Для якого виконується умова: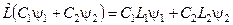 
;
б) Для якого виконується умова: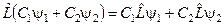 
;
в) Для якого виконується умова: 
.
22. Яким умовам повинна задовольняти хвильова функція внаслідок її фізичних обмежень?
а) однозначність, неперервність і квадратично інтегрованість;
б) однозначність, неперервність, диференційованість і інтегрованість;
в) однозначність, неперервність, самоспряженість і квадратично інтегрованість.
23. Що означає твердження „власне значення ермітового оператора вироджене”?
а) Власне значення ермітового оператора називають виродженим, якщо йому відповідає кілька лінійно залежних власних функцій, що відповідають умові нормування.
б) Власне значення ермітового оператора називають виродженим, якщо йому відповідає кілька лінійно залежних власних функцій, що відповідають стандартним умовам.
в) Власне значення ермітового оператора називають виродженим, якщо йому відповідає кілька лінійно незалежних власних функцій.
24. Як визначити середнє значення фізичної величини із урахуванням імовірності їх дозволених значень.
а)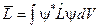 
, якщо 
.
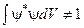б)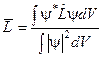 
, якщо .
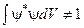в) 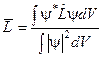, якщо 
.
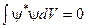25. Чому дорівнює оператор координати?
а)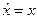 
. б) 
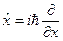. в)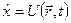 
.
26. Записати стаціонарне рівняння Шредінгера в операторному представленні.
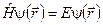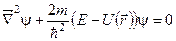а) . б) . в) .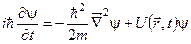
27. За яких умов можна стверджувати, що квантовий рух переходить в класичний?
а) Квантовий рух переходить у класичний, якщо кінетична енергія частинки мала, а зовнішнє силове поле змінюється неперервно.
б) Квантовий рух переходить у класичний, якщо кінетична енергія частинки велика, а зовнішнє силове поле змінюється плавно.
в) Квантовий рух переходить у класичний, якщо кінетична енергія частинки велика, а зовнішнє силове поле змінюється швидко.
28. Який рух квантової частинки називають одновимірним?
а) Одновимірний рух – це такий рух квантової частинки, який описується хвильовою функцією, що є функцією лише однієї координати.
б) Одновимірний рух – це такий рух квантової частинки, коли вона знаходиться в стаціонарному полі, що є функцією лише однієї координати.
в) Одновимірний рух – це такий рух квантової частинки, який описується стаціонарною хвильовою функцією, що є функцією лише однієї координати.
29. Який стан квантової системи називають стаціонарним?
а) Стан квантової системи називають стаціонарним, якщо зовнішнє силове поле в якому вона перебуває не залежить від часу.
б) Стан квантової системи називають стаціонарним, якщо хвильова функція, що описує такий стан не залежить від часу.
в) Стан квантової системи називають стаціонарним, якщо зовнішнє силове поле в якому вона перебуває є залежною від часу.
30. Співвідношення невизначеностей Гейзенберга випливає з того, що:
а) хвилі де Бройля –це хвилі ймовірності; квадрат модуля хвилі де Бройля зв’язаний з ймовірністю місцезнаходження частинки.
б) мікрооб’єктам притаманний корпускулярно-хвильовий дуалізм.
в) основні характеристики мікрооб’єктів можуть набувати дискретних значень: енергія, імпульс тощо.
31. Який розділ фізики називають квантовою теорією поля?
а) Фундаментальну фізичну теорію, що вивчає рух та взаємодію макрочастинок в зовнішніх силових полях при швидкостях менших за швидкість світла.
б) Фундаментальну фізичну теорію, що вивчає рух та взаємодію мікрочастинок в зовнішніх силових полях при швидкостях менших за швидкість світла.
в) Фундаментальну фізичну теорію, що вивчає рух та взаємодію мікрочастинок в зовнішніх силових полях за будь-яких швидкостей руху досліджуваних мікрооб’єктів.
32. У чому полягає ідея Ейнштейна стосовно пояснення квантового характеру електромагнітного випромінювання?
а) Оскільки характер випромінювання абсолютно чорного тіла не залежить від його будови, тому пропонується замінити атоми і молекули твердого тіла системою гармонійних осциляторів, що випромінюють і поглинають енергію. Ідея Ейнштейна полягає у тому, що рівні енергії осциляторів дискретні.
б) Оскільки характер випромінювання абсолютно чорного тіла не залежить від його будови, тому пропонується замінити атоми і молекули твердого тіла системою гармонійних осциляторів, що випромінюють і поглинають енергію. Ідея Ейнштейна полягає у тому, що осциляторів не просто поглинає та випромінює дискретно, а саме випромінювання існує у вигляді окремих дискретних порцій.
в) Оскільки характер випромінювання абсолютно чорного тіла не залежить від його будови, тому пропонується замінити атоми і молекули твердого тіла системою гармонійних осциляторів, що випромінюють і поглинають енергію. Ідея Ейнштейна полягає у тому, що випромінювання – це своєрідний набір мікрооб’єктів, що мають подвійний характер, тобто володіють корпускулярно-хвильовим дуалізмом.
33. У чому полягає фізичний зміст сталої Планка?
а) В природі існує обмеження на мінімальне значення будь-якого впливу на матеріальний об’єкт, стала Планка – це універсальна кількісна характеристика такого мінімального впливу.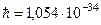 
Дж·с.
б) В природі існує обмеження на максимальне значення будь-якого впливу на матеріальний об’єкт, стала Планка – це універсальна кількісна характеристика такого максимального впливу. 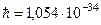Дж·с.
в) Коли об’єкт такий, що мінімальним впливом можна знехтувати, то це – мікротіло, коли ж мінімальним впливом на об’єкт знехтувати не можна – то це макрооб’єкт. Стала Планка розмежовує макро- і мікросвіт.
34. Які фізичні явища вказують на хвильову природу мікрооб’єктів?
а) інтерференція і дифракція; б) фотоефект, ефект Компотна; в) теорія Бора.
35. Як визначається групова швидкість хвиль де Бройля?
а)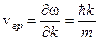 
; б) 
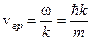; в) 
.
36. Що називають комутатором операторів?
а) Комутатор двох операторів позначається символом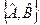 
і визначається за правилом 
.
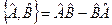б) Комутатор двох операторів позначається символом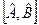 
і визначається за правилом 
.
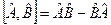в) Комутатор двох операторів позначається символом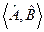 
і визначається за правилом 
.
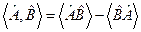37. Як визначається густина імовірності місцезнаходження мікрочастинки?
а) Квадрат модуля хвильової функції рівний густині імовірності місцезнаходження частинки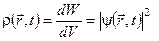 
, за умови нормування хвильової функції: 
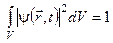. Якщо умова нормування не виконується густину імовірності визначити не можна.
б) Квадрат модуля хвильової функції рівний густині імовірності місцезнаходження частинки 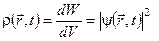, за умови нормування хвильової функції: 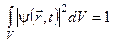. Якщо умова нормування не виконується, густину імовірності визначається із співвідношення: 
.
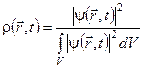в) Квадрат модуля хвильової функції рівний густині імовірності місцезнаходження частинки 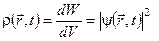, за умови нормування хвильової функції: 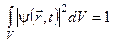. Якщо умова нормування не виконується, густину імовірності визначається із співвідношення: 
.
38. Чому серед величезної різноманітності операторів в математиці, в кантовій механіці використовують лише самоспряжені (ермітові) оператори?
а) Тому, що власні значення ермітових операторів комплексні числа.
б) Тому, що власні значення ермітових операторів дійсні числа.
в) Тому, що власні функції ермітових операторів задовольняють стандартним умовам.
39. Що у квантовій механіці розуміють під повним набором спостережуваних?
а) Повний набір спостережуваних – це ті фізичні величини, які для даної системи можуть мати одночасно точні, певні значення.
б) Повний набір спостережуваних – це ті фізичні квантово-механічні величини, які для даної системи не можуть мати одночасно точні, певні значення.
в) Повний набір спостережуваних – це набір квантових чисел, які для даної системи не можуть мати одночасно точні, певні значення.
40. Який вигляд має оператор проекції імпульсу на вісь 
?
а)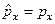 
. б) 
. в)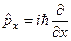 
.
41. Записати квантові дужки Пуассона.
а)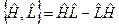 
. б) 
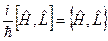. в) 
.
42. Записати рівняння неперервності квантової механіки.
а)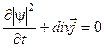 
. б) 
. в)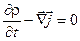 
.
43. Записати інтегральну форму стаціонарного рівняння Шредінгера для часової складової хвильової функції.
а)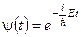 
. б) 
. в)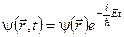 
.
44. Рівняння для власних функцій і власних значень оператора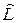 
має вигляд:
а)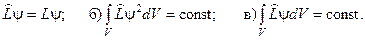 
45. Оператор моменту імпульсу мікрочастинки можна подати як:
а)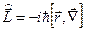 
; б) 
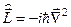; в)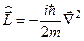 
.
46. Сформулювати принцип відповідності для квантової теорії.
а) Квантова механіка включає в себе класичну механіку як граничний випадок: при переході від мікрооб’єктів до макрооб’єктів закони квантової механіки переходять в класичні.
б) У квантовій механіці існує однозначна динамічна закономірність для хвильової функції, через яку однозначно визначається густина імовірності місцезнаходження частинки, а не саме місцезнаходження. Отже, однозначно зв’язані не самі стани, а їх потенціальні можливості.
в) У квантовій механіці всі величини, що спостерігаються описуються лінійними самоспряженими операторами.
47. Сформулювати перший постулат теорії Бора.
а) Випромінювання і поглинання енергії атомами відбувається при його стрибкоподібному переході з одного стаціонарного стану в інший: .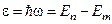
б) Існують стаціонарні стани атома, в яких його енергія не змінюється, а він не випромінює і не поглинає: .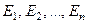
в) Для того, щоб з усіх можливих квантових станів енергії відшукати стаціонарні використовують правило квантування стаціонарних орбіт: ,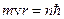
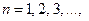
48. Записати співвідношення неозначеностей Гейзенберга у координатному представленні.
а) 
; б) 
; в)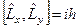 
.
49. Які фундаментальні експериментальні дослідження вперше підтвердили ідею Луї де Бройля щодо корпускулярно-хвильового дуалізму елементарних частинок?
а) Дифракцію протонів і нейтронів вперше спостерігали Вульф та Брегг (1923 р.) під час їх пружного розсіювання на атомах та атомних ядрах.
б) Дифракція мікрочастинок вперше була виявлена експериментально в досліді американських фізиків К. Девісона і Л. Джермера (1927 р). В цьому досліді електрони, прискорювались електричним полем, відбивались від кристалографічної поверхні нікелю, що оберталася. При певних кутах повороту виникали максимуми, що реєструвались за допомогою гальванометра під різними кутами відхилення від першопочаткового напрямку пучка електронів та при різних прискорюючи напругах.
в) У 1925 році Дж. Уленбек і С. Гаудсміт вперше спостерігали дифракцію атомів і молекул, які знаходяться в газоподібному стані в посудині при абсолютній температурі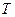 
, якій відповідає довжина хвилі 
.
50. Чи має фізичний зміст групова швидкість для плоскої монохроматичної хвилі де Бройля, у чому полягає ідея введення цієї величини?
а) Фізичного змісту групова швидкість для плоскої монохроматичної хвилі де Бройля не має, бо плоска хвиля одна, але у квантовій механіці пропонується замінити плоску хвилю пакетом хвиль, який і переміщуватиметься у просторі із груповою швидкістю, ця концепція врахує імовірнісну поведінку мікрооб’єктів.
б) Фізичного змісту групова швидкість для плоскої монохроматичної хвилі де Бройля не має, бо плоска хвиля одна, але у квантовій механіці пропонується замінити плоску хвилю пакетом хвиль, який і переміщуватиметься у просторі із груповою швидкістю, ця концепція врахує динамічні закономірності поведінки мікрооб’єктів.
в) Фізичний зміст групова швидкість для плоскої монохроматичної хвилі де Бройля має і її значення визначається з формули .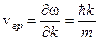
51. Які оператори називають комутуючими?
а) Коли комутатор двох операторів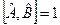 
.
б) Коли комутатор двох операторів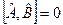 
.
в) Коли комутатор двох операторів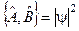 
.
52. Запишіть умову нормування хвильової функції.
а) 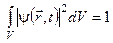; б) 
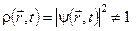; в) .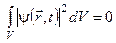
53. Які типи спектрів власних значень ермітових операторів Ви знаєте?
а) дискретний, неперервний, неперервно-дискретний;
б) лінійчатий, неперервний, смугастий;
в) дифракційний, інтерференційний.
54. Як у квантовій механіці описується квантово-механічний стан мікрочастинок?
а) Стан квантової частинки описується хвильовою функцією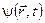 
, вигляд цієї функції та її зміну шукають за допомогою квантового рівняння руху.
б) Стан квантової частинки описується хвильовою функцією 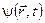, вигляд цієї функції та її зміну шукають за допомогою рівняння Шредінгера.
в) Стан квантової частинки описується квадратом модуля хвильової функції 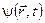, вигляд цієї функції та її зміну шукають за допомогою стаціонарного рівняння Шредінгера.
55. Записати загальний вигляд оператора Гамільтона?
а)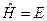 
. б) 
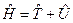. в) 
.
56. Записати квантове рівняння руху?
а) 
. б) 
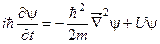. в) .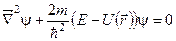
57. Як визначає густина потоку імовірностей?
а)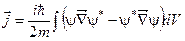 
. б) 
. в)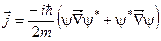 
.
58. Сформулюйте основні властивості одновимірного руху.
а) Хвильову функцію шукають з одновимірного стаціонарного рівняння Шредінгера; хвильові функції дискретного спектру при одновимірному русі невироджені; якщо повна енергія частинки менша за зовнішнє потенціальне поле, то її рух фінітний, а енергетичний спектр – дискретний.
б) Хвильову функцію шукають з стаціонарного рівняння Шредінгера для вільної частинки; хвильові функції дискретного спектру при одновимірному русі вироджені; якщо повна енергія частинки більша за зовнішнє потенціальне поле, то її рух інфінітний, а енергетичний спектр – неперервний.
в) Хвильову функцію шукають з одновимірного рівняння Шредінгера; хвильові функції дискретного спектру при одновимірному русі невироджені; якщо повна енергія частинки менша за зовнішнє потенціальне поле, то її рух інфінітний, а енергетичний спектр – дискретний.
59. Квантовий рух переходить у класичний, якщо:
а) енергія частинки мала: 
, а силове поле змінюється плавно;
б) енергія частинки велика: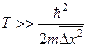 
, а силове поле змінюється плавно;
в) енергія частинки велика: 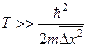, а силове поле змінюється швидко.
60. Співвідношення неозначеностей Гейзенберга носять загальний характер і для будь-якої пари спряжених квантово-механічних величин має вигляд:
а)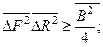 
б) 
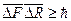; в)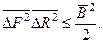 
61. Сформулювати квантово-механічний принцип суперпозиції.
а) Якщо мікрооб’єкт може знаходитись у квантових станах, що описуються хвильовими функціями 
, то густина імовірності відшукання такого об’єкта визначається квадратом модуля функцій співмножників: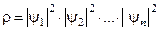 
.
б) У квантовій механіці існує однозначна динамічна закономірність для хвильової функції, через яку однозначно визначається густина імовірності місцезнаходження частинки, а не саме місцезнаходження. Отже, однозначно зв’язані не самі стани, а їх потенціальні можливості.
в) Якщо мікрооб’єкт або атомна система може знаходитись в станах, що описуються хвильовими функціями , то вона може знаходитись в стані, що описується хвильовою функцією типу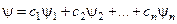 
.
62. Сформулювати другий постулат теорії Бора.
а) Випромінювання і поглинання енергії атомами відбувається при його стрибкоподібному переході з одного стаціонарного стану в інший: .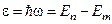
б) Існують стаціонарні стани атома, в яких його енергія не змінюється, а він не випромінює і не поглинає: .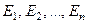
в) Для того, щоб з усіх можливих квантових станів енергії відшукати стаціонарні використовують правило квантування стаціонарних орбіт: ,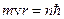
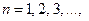
63. У чому полягає ідея Луї де Бройля, щодо прояву корпускулярно-хвильового дуалізму мікрооб’єктів?
а) У 1923 р. Л. Де Бройля висунув ідею про те, що корпускулярно-хвильовий дуалізм притаманний не лише світловим але й елементарним частинкам (електронам, протонам, молекулам і т.п.), причому хвильові характеристики частинок: частота, хвильовий вектор, довжина хвилі пов’язані з імпульсом або енергією частинок.
б) У 1923 р. Л. Де Бройля висунув ідею про те, що світло – це своєрідний набір мікрооб’єктів, що мають подвійний характер, тобто володіють корпускулярно-хвильовим дуалізмом.
в) У 1923 р. Л. Де Бройля висунув ідею про те, що для узгодження корпускулярних і хвильових проявів мікрооб’єктів необхідно, виходячи з концепції математичних хвиль, які описують їх хвильові властивості, замінити плоску хвилю пакетом хвиль.
64. Як розрахувати довжину хвилі де Бройля?
а) 
; б) 
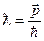; в)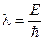 
.
65. У чому полягає необхідність статистичної інтерпретації квантових явищ?
а) Результати дослідів по виявленню корпускулярних властивостей мікрочастинок свідчать про їх корпускулярну природу, а тому їх поведінку наперед передбачити неможливо, бо вони описуються не динамічними , а статистичними закономірностями.
б) Результати дослідів по виявленню хвильових властивостей мікрочастинок свідчать про їх хвильову природу, а тому їх поведінку наперед передбачити неможливо, бо вони описуються не динамічними , а статистичними закономірностями.
в) Результати дослідів по виявленню хвильових властивостей мікрочастинок свідчать про їх хвильову природу, а тому їх поведінку наперед передбачити завжди можливо і вони описуються за відповідних умов або динамічними , або статистичними закономірностями.
66. Співвідношення неозначеностей Гейзенберга носять загальний характер і для будь-якої пари спряжених квантово-механічних величин має вигляд:
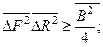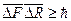а) б) ; в)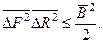
67. Який оператор називають самоспряженим?
а) Якщо він задовольняє співвідношенню: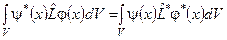 
.
б) Якщо він задовольняє співвідношенню: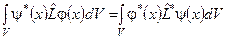 
.
в) Якщо він задовольняє співвідношенню: 
.
68. Сформулюйте квантово-механічний принцип суперпозиції.
а) Якщо частинка може знаходитись в стані 
та 
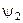, то вона може знаходитись і в стані 
, де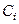 
– комплексні числа, для яких 
.
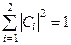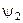б) Якщо частинка може знаходитись в стані та , то вона може знаходитись і в стані 
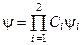, де 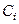– комплексні числа, для яких 
.
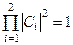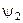в) Якщо частинка може знаходитись в стані та , то вона може знаходитись і в стані , де 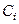– дійсні числа, для яких .
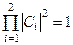69. Які властивості власних функцій ермітових операторів Вам відомі?
а) Власні функції ермітових операторів попарно колінеарні та володіють властивістю повноти, що дає можливість подати її для дискретного спектру власних значень у вигляді ряду Тейлора, для неперервного – як інтеграл Фур’є.
б) Власні функції ермітових операторів попарно ортогональні та володіють властивістю повноти, що дає можливість подати її для дискретного спектру власних значень у вигляді ряду Фур’є, для неперервного – як ряд Тейлора.
в) Власні функції ермітових операторів попарно ортогональні та володіють властивістю повноти, що дає можливість подати її для дискретного спектру власних значень у вигляді ряду Фур’є, для неперервного – як інтеграл Фур’є.
70. З якого рівняння квантової механіки шукають хвильову функцію мікрочастинки та її зміну? Записати його загальний вигляд.
а) За допомогою стаціонарного рівняння Шредінгера: 
.
б) За допомогою квантового рівняння руху: .
в) За допомогою основного рівняння Шредінгера: .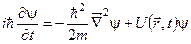
71. Який вигляд має оператор кінетичної енергії?
а)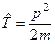 
. б) 
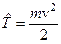. в)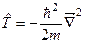 
.
72. Записати квантове рівняння руху в формі Гейзенберга.
а)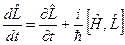 
. б) 
. в) .
73. Як визначається середня густина речовини?
а)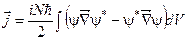 
. б) 
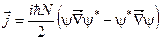. в)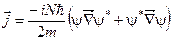 
.
74. Який стан квантової системи називають стаціонарним?
а) Стан квантової системи називають стаціонарним, якщо зовнішнє силове поле в якому вона перебуває не залежить від часу.
б) Стан квантової системи називають стаціонарним, якщо хвильова функція, що описує такий стан не залежить від часу.
в) Стан квантової системи називають стаціонарним, якщо зовнішнє силове поле в якому вона перебуває є залежною від часу.
75. Записати стаціонарне рівняння Шредінгера для координатної частини хвильової функції в диференціальній формі.
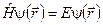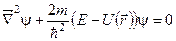а) . б) . в) .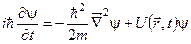
Завдання №2 (0,75 бали за кожне)
1. Відшукати квантове число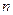 
збудженого стану атома водню, якщо відомо, що при переході до основного стану атом випромінює два фотони з довжинами хвиль 
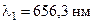і 
.
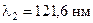Відповідь: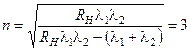 
.
2. Оцінити енергію основного стану осцилятора, скориставшись співвідношенням неозначеностей Гейзенберга , де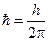 
, риска зверху позначає середнє значення.
Відповідь: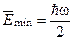 
.
3. Відшукати квантове число 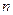збудженого стану і радіус відповідної борівської орбіти електрона в атомі водню, якщо відомо, що при переході до основного стану атом випромінює фотон з довжиною хвилі і 
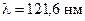. Сталу Ридберга прийняти рівною 109737б31 см-1.
Відповідь: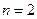 
; 
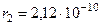м.
4. Кінетична енергія релятивістської частинки дорівнює 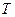, її маса спокою 
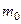. Яка дебройлівська довжина хвилі цієї частинки?
Відповідь: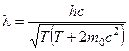 
.
5. Відшукати сталу Ридберга, якщо відомо, що різниця довжин хвиль між головною лінією серії Бальмера і резонансною лінією іона гелію 
дорівнює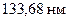 
.
Відповідь: 
см-1.
6. Розрахувати довжину хвилі де Бройля молекули кисню, що рухається із середньою тепловою швидкістю при температурі 300 К.
Відповідь: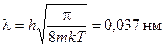 
.
7. Вважаючи, що 
частинки з кінетичною енергією 8 МеВ взаємодіють з ядрами свинцю за законом Кулона. Оцінити зовнішню межу радіуса ядра свинцю.
Відповідь: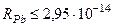 
м.
8. Розрахувати довжину хвилі де Бройля протона, кінетична енергія якого дорівнює середній кінетичній енергії теплового руху одноатомних молекул при кімнатній температурі.
Відповідь: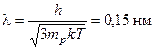 
.
9. Відшукати довжину хвилі фотона, що випромінюється при переході електрона у двократно іонізованому атомі літію з другої борівської орбіти на першу.
Відповідь: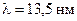 
.
10. У 1929 р. Естерман і Штерн виконали експеримент з дифракції атомів гелію, що падали на кристал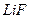 
. Яка довжина хвилі де Бройля атома гелію з енергією 
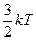при температурі 290 К?
Відповідь: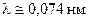 
.
Завдання №3 (1 бал за кожне)
1. Перевірити наступну операторну рівність: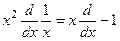 
.
2. Відшукати власне значення оператора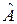 
, що належить власній функції 
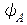, якщо: 
.
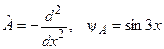Відповідь: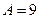 
.
3. Перевірити наступну рівність для комутаторів: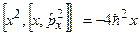 
.
4. Розрахувати середнє значення кінетичної енергії квантового осцилятора з частотою 
в основному стані 
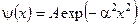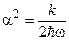, де 
, де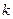 
– стала 
.
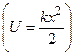Відповідь: з умови нормування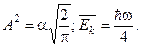 
5. Перевірити наступну операторну рівність: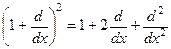 
.
6. Відшукати власне значення оператора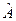 
, що належить власній функції 
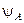, якщо: 
.
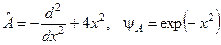Відповідь: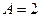 
.
7. Перевірити наступну рівність для комутаторів: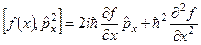 
.
8. Відшукати власне значення оператора 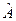, що належить власній функції 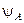, якщо: 
.
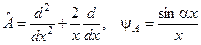Відповідь: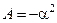 
.
9. Перевірити наступну операторну рівність: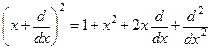 
.
10. В деякий момент часу частинка знаходиться в квантовому стані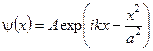 
, де 
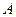і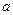 
– сталі. Відшукати середнє значення координати 
.
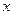Відповідь: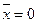 
.