Общие свойства функции распределения
Теорема.Любая функция распределения обладает следующими свойствами:
(F1) она не убывает: если 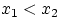 , то
, то 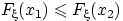 ;
;
(F2) существуют пределы 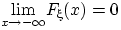 и
и 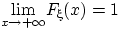 ;
;
(F3) она в любой точке непрерывна слева: 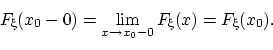
Доказательство
Доказательство свойства (F1). Для любых чисел 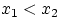 событие
событие 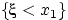 влечёт событие
влечёт событие 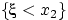 , т.е.
, т.е. 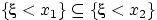 . Но вероятность — монотонная функция событий, поэтому
. Но вероятность — монотонная функция событий, поэтому
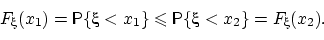
Для доказательства остальных свойств нам понадобится свойство непрерывности вероятностной меры.
Доказательство свойства (F2). Заметим сначала, что существование пределов в свойствах (F2), (F3) вытекает из монотонности и ограниченности функции 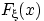 . Остается лишь доказать равенства
. Остается лишь доказать равенства
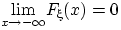 ,
, 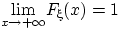 и
и 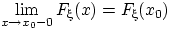 .
.
Для этого в каждом случае достаточно найти предел по какой-нибудь подпоследовательности 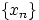 , так как существование предела влечёт совпадение всех частичных пределов.
, так как существование предела влечёт совпадение всех частичных пределов.
Докажем, что 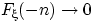 при
при 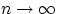 . Рассмотрим вложенную убывающую последовательность событий
. Рассмотрим вложенную убывающую последовательность событий 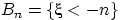 :
:
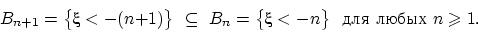
Пересечение 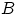 всех этих событий состоит из тех и только тех
всех этих событий состоит из тех и только тех 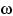 , для которых
, для которых 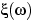 меньше любого вещественного числа. Но для любого элементарного исхода
меньше любого вещественного числа. Но для любого элементарного исхода 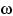 значение
значение 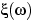 вещественно, и не может быть меньше всех вещественных чисел. Иначе говоря, пересечение событий
вещественно, и не может быть меньше всех вещественных чисел. Иначе говоря, пересечение событий 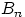 не содержит элементарных исходов, т.е.
не содержит элементарных исходов, т.е. 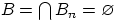 . По свойству непрерывности меры,
. По свойству непрерывности меры, 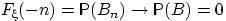 при
при 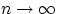 .
.
Точно так же докажем остальные свойства.
Покажем, что 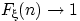 при
при 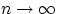 , т.е.
, т.е. 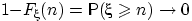 . Обозначим через
. Обозначим через  событие
событие 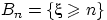 . События
. События 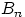 вложены:
вложены:
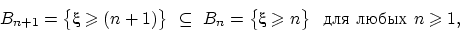
а пересечение 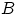 этих событий снова пусто — оно означает, что
этих событий снова пусто — оно означает, что 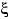 больше любого вещественного числа. По свойству непрерывности меры,
больше любого вещественного числа. По свойству непрерывности меры, 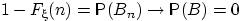 при
при 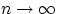 .
.
Доказательство свойства (F3). Достаточно доказать, что 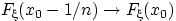 при
при 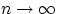 . Иначе говоря, доказать сходимость к нулю следующей разности:
. Иначе говоря, доказать сходимость к нулю следующей разности:
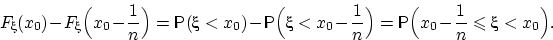
Зависимость функции распределения от макроскопического состояния
Окружающей среды
Функция распределения равновесной системы параметрически зависит от макроскопического состояния окружающей среды и не зависит от того, с помощью какого микросостояния это макросостояние окружающей среды реализуется.
В данном состоянии термодинамического равновесия, т.е. при данных конкретных значениях внешних термодинамических параметров и температуры, явный вид функции распределения нашей системы вполне определенный. Однако если теперь поместить наше тело в другое состояние термодинамического равновесия, которое определяется другими значениями внешних термодинамических параметров или температуры, то явных вид функции распределения нашей системы изменится.
Задать микроскопическое состояние системы - значит указать все ее координаты и импульсы системы.
Задать макроскопическое состояние системы - значит указать ее макроскопические параметры, такие как давление, температура , объем и т.д.
Параметры называются внешними, если они определяются положением, не входящих в нашу систему внешних тел. Объем системы, величина поверхности определяются расположением внешних тел. Напряжение силового поля зависит от положения источников поля – зарядов и токов, не входящих в систему.
Параметры называются внутренними, если они определяются совокупным движением и распределением в пространстве тел и частиц, входящих в нашу систему. Плотность, давление, энергия – внутренние параметры. Естественно, что величины внутренних параметров зависят от внешних параметров.
Внешниепараметры (объем газа в сосуде) есть функции координат идеализированных источников этих внешних силовых полей. Подчеркну, что по самому своему смыслу внешние параметры не зависят от координат и импульсов самой изучаемой системы.
Под внутренними параметрами (давление газа на стенки сосуда) системы понимают средние значения любых функций координат и импульсов самой этой системы.
Температура не относится ни к внешним, ни к внутренним параметрам. Она у нас будет стоять особняком.
В термодинамическом равновесии все внутренние параметры системы являются функцией внешних параметров и температуры. Другими словами, макроскопическое состояние системы, находящейся в равновесии со своим окружением, задается внешними параметрами и температурой.
Договоримся о следующих обозначениях, которые будем везде в дальнейшем использовать Совокупность координат и импульсов изучаемой нами системы мы будем обозначать 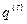 и
и 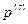 . Совокупность координат и импульсов окружающей среды будем обозначать
. Совокупность координат и импульсов окружающей среды будем обозначать 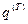 и
и 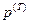 . Совокупность всех внешних параметров, задающих состояние равновесия нашей системы, будем обозначать буквой
. Совокупность всех внешних параметров, задающих состояние равновесия нашей системы, будем обозначать буквой 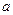 . Один- i-ый - внешний параметр будем обозначать
. Один- i-ый - внешний параметр будем обозначать 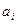 (буквой
(буквой 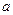 с индексом i).
с индексом i).
При рассмотрении системы, находящейся в равновесии с окружающей средой, мы очень-очень сложную точную функцию Гамильтона замкнутой системы, состоящей из изучаемого тела и окружающей среды, заменяем на приближенную, которую представляем в виде суммы эффективной функции Гамильтона нашей системы и эффективной функции Гамильтона окружающей среды. Т.е. мы пишем, что
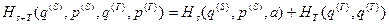 .
.
Теплообменмежду нашей системой и окружающей средой мы учитываем следующим образом. Мы фиксируем функцию Гамильтона 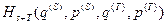 всей замкнутой системы, но при этом мы не фиксируем по отдельности гамильтониан нашей системы
всей замкнутой системы, но при этом мы не фиксируем по отдельности гамильтониан нашей системы 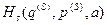 и гамильтониан окружающей среды
и гамильтониан окружающей среды 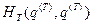 . Этим мы оставляем возможность теплообмена между нашей системой и окружающей средой. В результате мы получаем, что различные значения энергии нашей системы могут реализовываться с различной вероятностью, которая определяется температурой.
. Этим мы оставляем возможность теплообмена между нашей системой и окружающей средой. В результате мы получаем, что различные значения энергии нашей системы могут реализовываться с различной вероятностью, которая определяется температурой.
Теплообмен — это процесс изменения внутренней энергии без совершения работы над телом или самим телом.
Теплообмен всегда происходит в определенном направлении: от тел с более высокой температурой к телам с более низкой.
Когда температуры тел выравниваются, теплообмен прекращается.
Теплообмен может осуществляться тремя способами:
- теплопроводностью
- конвекцией
- излучением
4. Микроканоническое распределения Гиббса в классической статистической теории
Рассмотрим ситуацию, когда изучаемая система является адиабатически изолированной от окружающей среды или, иначе, замкнутой. система не обменивается с окружающей средой ни частицами, ни энергией. При таком задании нашей системы мы фиксируем число частиц в ней 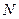 , ее объем
, ее объем 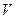 и остальные внешние параметры
и остальные внешние параметры 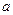 , а также ее энергию. Причем речь идет не о внутренней энергии, а именно об энергии в обычном механическом понимании.
, а также ее энергию. Причем речь идет не о внутренней энергии, а именно об энергии в обычном механическом понимании.
Состояние равновесия такой системы задается внешними параметрами и ее энергией. Для полноты информации – для того, чтобы написать функцию Гамильтона нашей системы - нам еще, конечно же, нужно знать число частиц N в нашей системе.
Распределение вероятности различных микросостояний замкнутой системы называется микроканоническим.
Вид функции распределения для адиабатически изолированной системы непосредственно вытекает из постулата, который носит название принципа равной вероятности. Этот принцип состоит в следующем. Состояние равновесия нашей замкнутой системы задается ее энергией Е. Функция Гамильтона системы есть ни что иное, как ее полная энергия. Следовательно, микросостояния нашей системы, возможные в заданном состоянии равновесия, определяются условием
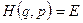 . (1)
. (1)
Никакие другие микросостояния нашей системы в этом ее состоянии равновесия не возможны. Утверждение постулата равной вероятности состоит в том, что с равной вероятностью реализуется любое микросостояние, возможное в данном состоянии равновесия изолированной системы.
Непосредственно из постулата равной вероятности следует, что функция распределения нашей замкнутой системы имеет вид
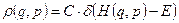 . (2)
. (2)
Действительно, пусть энергия нашей системе является не строго постоянной, а может меняться в очень малом интервале от 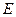 до
до 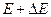 . Тогда возможные микросостояния нашей системы определяются условием
. Тогда возможные микросостояния нашей системы определяются условием
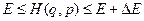 . (3)
. (3)
Пусть ширина интервала энергии 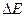 хоть и конечна, но настолько мала, что для нашей системы с большой точностью справедлив принцип равной вероятности. Т.е. ширина интервала настолько мала, что каждое микросостояние, энергия которого попадает в данный интервал, реализуется с равной вероятностью. Другими словами, функция распределения нашей системы имеет вид
хоть и конечна, но настолько мала, что для нашей системы с большой точностью справедлив принцип равной вероятности. Т.е. ширина интервала настолько мала, что каждое микросостояние, энергия которого попадает в данный интервал, реализуется с равной вероятностью. Другими словами, функция распределения нашей системы имеет вид
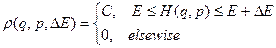 , (4)
, (4)
где С – константа.
Равновесное значение макроскопического параметра, как мы значем, есть
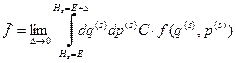 . (5)
. (5)
Теперь для того, чтобы перейти от квазизамкнутой системы к истинно замкнутой, мы должны устремить 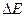 к нулю. В результате мы получим наш внутренний макроскопический параметр
к нулю. В результате мы получим наш внутренний макроскопический параметр
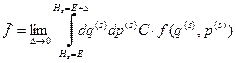 . Согласно определению дельта-функции Дирака этот предел равен
. Согласно определению дельта-функции Дирака этот предел равен
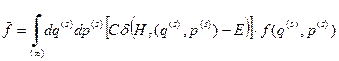 . (6)
. (6)
Таким образом, функцию распределения адиабатически изолированной системы мы можем написать как произведение нормировочной постоянной на дельта-функцию Дирака, аргумент которой есть разность функции Гамильтона нашей системы и энергии E
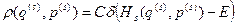 .
.
Значение постоянной 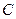 определяется условием нормировки
определяется условием нормировки
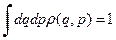 . (7)
. (7)
Подставляем в условие нормировки явный вид функции распределения и переходим от интегрирования по фазовому пространству к интерированию по энергии в соответствии с той теоремой, которую сформулированной на прошлой лекции. В результате получим
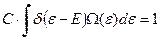 , (8)
, (8)
где
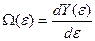 , (9)
, (9)
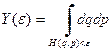 (10)
(10)
объем фазового пространства, ограниченный поверхностью постоянной энергии 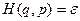 .
.
Воспользовавшись основным свойством дельта-функции
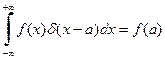 . (11)
. (11)
В результате получаем
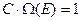 . (12)
. (12)
Отсюда постоянная 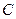 есть
есть
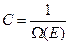 .
.
