Гипотеза Луи де Бройля. 1924 г.
Известно, что фотон обладает свойствами волны и частицы. Луи де Бройль выдвигает гипотезу, что любая частица вещества (электрон, например) также обладает свойствами волны и частицы, то есть наличие волновых и квантовых свойств является общим универсальным свойством всей материи.
Для электрона можно записать формулу фотона:
; p=mV
Момент импульса есть вектор!
; 
В обычных электронных приборах напряжение меняется от 1 до 104 В. следовательно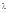 
=(12-0,12) 
.
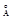Для проведения опытов по дифракции с электронным пучком, в качестве дифракционной решетки надо взять кристаллическую решетку, в которой расстояние между узлами соизмеримо с несколькими ангстремами (6-8).
Опыт Тартаковской. Рис.1.6.
Так как распределение электронов на экране, соответствующее ходу кривой интенсивности при дифракции, устанавливается только при большом числе прошедших электронов, то волновые свойства электронов следует объяснять статистически: интенсивность волны де Бройля пропорциональна вероятности обнаружения электрона в данном месте пространства. Поэтому волны де Бройля – есть волны вероятности, ибо они дают ответ на вопрос: какова вероятность того, что в данный момент времени частица находится в данном объеме пространства (волновые свойства света – это реальное поле определенной длины волны).
Энергия частицы отрицательна, волны дискретны.
2. Тот факт, что электрон, ударяясь об экран, вызывает вспышку только в одной точке, указывает на то, то электрон частица.
3. Частицы, которые явно обладают волновыми и квантовыми свойствами, называются микрочастицами. Наличие у них волновых свойств приводит к тому, что поведение их носит вероятностный характер.
4. Если говорить о пуле, вылетевшей из ружья, то в силу ее большой массы, 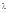, связанная с движением пули, будет очень маленькой ( 
). Следовательно, будет мала вероятность того, что пуля отклонится от траектории, рассчитанной для нее по законам Ньютона (макрочастица). Поведение пули носит достоверный характер.
5. Так как микрочастицы обладают волновыми свойствами и поведение их носит вероятностный характер, то, следовательно, основным уравнением их движения не может быть уравнение Ньютона.
Принцип неопределенности.
Постановка задачи. Классическая механика.
Эти характеристики достоверно известны одновременно в данный момент времени.
, px -проекция момта импульса на ось Х. 
сопряженные параметры
Можно ли таким же образом описывать поведение микрочастиц? Нет, так как природа процессов различная.
Ответ находят, рассматривая опыт по дифракции электронов на щели. Рис.1.7.
AB=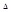 
x - ширина щели (расстояние между узлами кристаллической решетки).
Если на экране появилась вспышка, то можно утверждать, что электрон прошел щель. При этом ширина щели ( 
) есть неопределенность местонахождения электрона в момент прохождения щели.
Если сужать щель ( 
) то получим достоверное значение координаты х электрона в момент прохождения щели.
Благодаря волновым свойствам электрона можно утверждать, что электрон, пройдя щель, дальше движется внутри конуса с углом раствора 
.
-неопределенность px электрона при прохождении через щель. 
.
- угол первого дифракционного минимума на щели.
Итак.
1. Если , то есть х. 
– возрастает, 
-возрастает.
2. Если 
, то есть pх.
.
Следовательно, координата и спряженный импульс не могут быть одновременно неопределены не в силу технических невозможностей, а в силу того, что эти две величины не являются характеристиками микрочастицы потому что микрочастица, в отличие от классической частицы, обладает еще и волновыми свойствами. Как только мы хотим применить к микрочастице характеристики классической часитцы, возникает неопределенность.
Если все же хотим описать поведение микрочастицы с помощью координаты и сопряженного импульса, то это можно сделать только в следующих пределах:
С учетом дифракционных минимумов большего порядка соотношение будет следующим: 
- соотношение неопределенностей. Является следствием волновых свойств микрочастиц.
Соотношение неопределенностей поставили последнюю точку в споре о том, можно ли использовать законы Ньютона в микромире. Нет.