Раздел 6. основы молекулярной физики и термодинамики.

ТЕМЫ

Тема 1. Молекулярно-кинетические представления. Статическое распределение.

Пространство скоростей (v-пространство). Плоскость м-точек как функция модуля скоростей. Функция распределения вероятности значения v. Условия нормировки. Функция распределения Максвелла. Определение средней, среднеквадратической и наиболее вероятностной скоростей. Барометрическая формула. Функция распределения Больцмана. Распределение Максвелла-Больцмана.

Л. 1: § 12.107, § 12.106, § 12.109.

Тема 2. Термодинамическое описание системы.

Система. Параметры состояния. Релаксация. Равновесное и неравновесное состояние. Термодинамический процесс. Обратимые и необратимые процессы. Круговой процесс или цикл. Анализ циклических процессов. Классическая теория теплоёмкости идеального газа. Отклонение экспериментальных значений теплоёмкости газов от теоретических значений.

Л. 1: § 14.124

Тема 3. Первое начало термодинамики.

Внутренняя энергия термодинамической системы. Аддитивность внутренней энергии. Различные формулировки первого начала термодинамики. Внутренняя энергия и теплоёмкость. Политропические процессы.

Л. 1: § 13.121, § 12.104

Тема 4. Второе начало термодинамики. Теорема Нернста.

Невозможность создания “вечного двигателя” второго рода. Формулировка второго начала термодинамики по Клаузиусу и Томпсону. Цикл Карно. КПД необратимой и обратимой тепловой машины. Теорема Нернста. Флуктуации.

Л. 1: § 14.126, § 14.134, § 14.127

Тема 5. Энтропия. Термодинамическая и статическая трактовка энтропии.

Энтропия как термодинамический потенциал и характеристика состояния системы. Энтропия сложной системы. Энтропия смешанная. Парадокс Гиббса. Основные соотношения термодинамики. Статическая трактовка энтропии.

Л. 1: § 14.132, § 14.135, § 14.136

Литература [1,c.207-225, 227-306].

МЕТОДИЧЕСКИЕ УКАЗАНИЯ.

Темы данного раздела посвящены изучению молекулярно-кинетических представлений с позиции описания свойств большого числа молекул. Термодинамическое описание большого числа молекул обосновывается статическими закономерностями, всесторонне и глубоко рассматриваются первое и второе начало термодинамики.

В связи с развитием кибернетики новую трактовку получило понятие энтропии – как меры хаотического движения молекул, составляющих систему. В информационном плане важна негаэнтропия – как мера упорядочения информации и способа достижения нового значения в оптимальном варианте.

ОСНОВНЫЕ ФОРМУЛЫ.

Количество вещества однородного газа (в молях)

n = N / N_a, или n = m / M.

где N – число молекул газа; m – масса газа; М – молярная масса газа; N_a – постоянная Авогадро.

Если система представляет смесь нескольких газов, то количество вещества системы

n = n₁ + n₂ +…+ n_n = N₁/N_a + N₂/N_a + N₃/N_n + … + N_n/N_a, или

n = m₁/M₁ + m₂/M₂ + … + m_n/M_n,

где n_i, N_i, m_i, M_i - соответственно количество вещества, число молекул, масса, молярная масса i – компоненты смеси.

Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа):

pV = ( m / M )RT = nRT,

где m – масса газа;

М – молярная масса газа;

R – молярная газовая постоянная;

n - количество вещества;

Т – термодинамическая температура.

Опытные газовые законы, являющиеся частными случаями уравнения Менделеева – Клапейрона для изопроцессов:

1. закон Бойля – Мариотта (изотермический процесс – Т = const, m = const):

pV = const,

или для двух состояний газа:

p₁V₁ = p₂V₂,

2. закон Гей – Люссака (изобарный процесс – р = const, m = const):

v / T = const,

или для двух состояний:

V₁ / T₁ = V₂ / T₂,

3. закон Шарля (изохорный процесс – V = const, m = const):

р/Т = const,

или для двух состояний:

р₁/T₁ = р₂/T₂,

4. объединенный газовый закон (m = const):

pV/T = const или р₁V₁/T₁ = р₂V₂/T₂,

где р₁, V₁, T₁ – давление, объем и температура газа в начальном состоянии;

р₂, V₂, T₂ – те же величины в конечном состоянии.

Закон Дальтона, определяющий давление смеси газов:

р = р₁ + р₂ + … + р_n,

где р_i – парциальное давление компонентов смеси;

n – число компонентов смеси.

Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.

Молярная масса смеси газов:

M = (m₁ + m₂ + … + m_n)/(n₁ + n₂ + … + n_n),

где m_i – масса i – го компонента смеси;

n_i – число компонентов смеси;

n_i = m_i/M_i – количество вещества i-го компонента смеси.

Массовая доля w_i i-го компонента смеси газа (в долях единицы или процентах):

w_i = m_i/m,

где m – масса смеси.

Концентрация молекул:

n = N/V = N_Ar/M,

где N – число молекул, содержащихся в данной системе;

r – плотность вещества;

V – объем системы.

Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.

Основное уравнение кинетической теории газов:

р = 2/3 n <E_n>,

где <E_n> – средняя кинетическая энергия поступательного движения молекулы.

Средняя кинетическая энергия поступательного движения молекул:

<E_n> = 3/2 кТ,

где к – постоянная Больцмана.

Средняя полная кинетическая энергия молекулы:

< E_i > = i/2 кТ,

где i – число степеней свободы молекулы.

Зависимость давления газа от концентрации молекул и температуры:

р = nkT.

Скорости молекул:

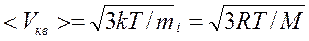(средняя квадратичная);

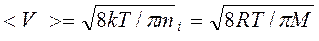(средняя арифметическая);

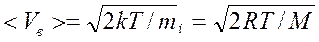(наиболее вероятная).

где m₁ – масса одной молекулы.

Относительная скорость молекулы: U = V/V_в,

где V – скорость данной молекулы.

Удельные теплоемкости газа при постоянном обьеме (С_V) и при постоянном давлении (С_Р):

С_V = (i/2)×(R/M); C_P = ((i + 2)/2)×(R/M).

Связь между удельной с и молярной С теплоемкостями:

с = С/М; С = сМ.

Уравнение Майера для молярных теплоемкостей:

С_Р – С_V = R.

Внутренняя энергия идеального газа:

U = (m/M)×(i/2)RT = (m/M)C_V×T.

Первое начало термодинамики:

Q = DU + A,

где Q – теплота сообщенная системе (газу):

DU – изменение внутренней энергии системы;

А – работа, совершенная системой против внешних сил.

Работа расширения газа:

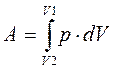(в общем случае)

А = р(V₂ – V₁) (при изобарном процессе);

А = (m/M)RTln(V₂/V₁) (при изотермическом процессе);

А = -DU = -(m/M)C_VDT при адиабатическом процессе),

где g = С_P/С_V – показатель адиабаты.

Уравнения Пуассона, связывающие параметры идеального газа при адиабатическом процессе:

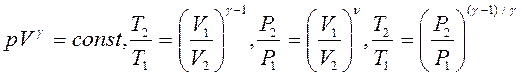
Термодинамический к.п.д. цикла:

h = (Q₁ – Q₂)/Q₁.

– теплота, полученная рабочим телом от теплоотдатчика (нагревателя);

Q₂ – теплота, переданная рабочим телом теплоприемнику (холодильнику).

Термодинамический к.п.д. Карно:

h = (Q₁ – Q₂)/Q₁ = (Т₁ – Т₂)/Т₁.

где Т₁ и Т₂ – термодинамические температуры теплоотдатчика и теплоприемника.

Коэффициент поверхностного натяжения:

a = F/1, или a = DE/DS,

где F – сила поверхностного натяжения, действующая на контур длины 1, ограничивающий поверхность жидкости;

DЕ – изменение свободной энергии поверхностной пленки жидкости, связанное с изменением площади DS поверхности этой пленки.

Формула Лапласа выражающая давление р, создаваемое сферической поверхностью жидкости:

р = 2a/R,

где R – радиус сферической поверхности.

Высота подъема жидкости в капиллярной трубке:

h = 2acos q/(rgR),

где q - краевой угол (q = 0 при полном смачивании стенок трубки жидкостью; q = p при полном не смачивании);

R – радиус канала трубки;

g – ускорение свободного падения.

Высота подъема жидкости между двумя близкими и параллельными друг другу плоскостями:

h = 2acos q/(rgd).

где d – расстояние между плоскостями.

ОСНОВНЫЕ ПОНЯТИЯ ТЕРМОДИНАМИКИ.

Макроскопическая система – всякий материальный объект. всякое тело, состоящее из большого числа частиц

Термодинамическое (ТД) состояние – совокупность значений некоторого числа физических величин, характеризующих физические свойства тела (системы тел) и определяющих состояние тела (системы тел).

Термодинамические параметры – физические величины, однозначно определяющие состояние тела (системы тел) (температура, плотность, теплоёмкость и т.п.).

Стационарное состояние системы тел – такое состояние, которое не меняется с течением времени.

Равновесное состояние – такое стационарное состояние, которое не обусловлено какими-либо явлениями происходящими с телами, внешними, по отношению к данному телу (системе).

Если в системе все параметры стационарны и, кроме того, нет никаких стационарных потоков за счет внешних источников, то такое состояние называется состоянием термодинамического равновесия (равновесным).

В равновесном состоянии тела:

1. Параметры его состояния равны соответствующим параметрам состояния внешней среды.

2. Параметры состояния (Р, ρ, Т) одинаковы во всех частях тела, находящихся при одном силовом воздействии. Например, Р, р, Т для всех частей небольшого объёма газа, находящегося в атмосфере на одной высоте, - одинаковы.

Термодинамическая система отличается от макроскопической тем, что она всегда находится в термодинамическом равновесии

Параметры состояния – такие ТД параметры, которые определяют равновесное состояние системы. Как правило, все ТД параметры системы в состоянии равновесия определяются параметрами состояния. Основными параметрами состояния химически однородной системы являются: удельный объём, давление и температура.

Давление – физическая величина, равная модулю силы, действующей не единицу площади поверхности тела, перпендикулярной к ней.

Удельный объём: v = 1/ρ; ρ – плотность.

Температура – параметр, характеризующий равновесие системы. С другой стороны, температура является величиной, характеризующей направление теплообмена между телами.

Уравнение состояния – связь между тремя основными параметрами.

Термодинамический процесс (ТДП) – всякое изменение состояния тела. В любом ТД процессе изменяются параметры, определяющие состояние тела.

Равновесным (квазистатическим) процессом называется ТДП при котором тело (система тел) проходит непрерывный ряд равновесных состояний (т.е. параметры системы не меняются скачкообразно).

При равновесном процессе, состояние тела должно изменятся бесконечно медленно. Это значит, что тело проходит через ряд бесконечно близких состояний равновесия с внешней средой. Все реальные ТДП протекают с конечной скоростью и, уже поэтому, являются неравновесными. Лишь в частных случаях неравновесностью реальных процессов можно пренебречь. Только равновесные процессы можно изобразить графически в координатах ТД параметров.

Неравновесный процесс изображается набором поверхностей в координатах P, V, T.